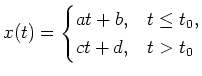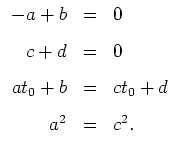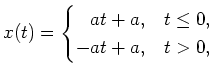Es sei
![$ \mbox{$x \in C_s^1[-1,1]$}$](img1.png) eine Funktion mit höchstens einer Ecke in dem Punkt
eine Funktion mit höchstens einer Ecke in dem Punkt
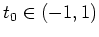 , die der
Eulerschen Differentialgleichung auf
, die der
Eulerschen Differentialgleichung auf
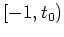 und
und
![$ \mbox{$(t_0,1]$}$](img4.png) genügt. Ferner erfülle
genügt. Ferner erfülle
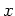 die 1. Weierstraß-Erdmannsche Eckenbedingung und die Randbedingungen.
Dann gilt aufgrund der Eulerschen Differentialgleichung:
Folglich ist
die 1. Weierstraß-Erdmannsche Eckenbedingung und die Randbedingungen.
Dann gilt aufgrund der Eulerschen Differentialgleichung:
Folglich ist
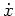 selbst konstant auf
selbst konstant auf
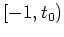 und auf
und auf
![$ \mbox{$(t_0,1]$}$](img4.png) . Damit ist
. Damit ist
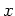 von der Form
mit gewissen Konstanten
von der Form
mit gewissen Konstanten
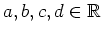 , die wir noch bestimmen möchten.
Da
, die wir noch bestimmen möchten.
Da
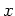 die 1. Weierstraß-Erdmannsche Eckenbedingung erfüllt, gilt ferner
Zusammen mit den Randbedingungen und der Stetigkeit von
die 1. Weierstraß-Erdmannsche Eckenbedingung erfüllt, gilt ferner
Zusammen mit den Randbedingungen und der Stetigkeit von
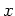 im Punkt
im Punkt
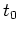 ergeben sich somit die folgenden Bedingungen
an die Variablen
ergeben sich somit die folgenden Bedingungen
an die Variablen
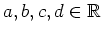 :
Diesem Gleichungssystem entnehmen wir, daß
:
Diesem Gleichungssystem entnehmen wir, daß
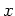 die folgende Gestalt besitzt:
mit einer beliebigen Konstanten
die folgende Gestalt besitzt:
mit einer beliebigen Konstanten
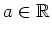 . Wir bemerken jedoch, daß diese Funktion für kein
. Wir bemerken jedoch, daß diese Funktion für kein
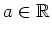 ein (schwaches) Minimum von
ein (schwaches) Minimum von
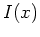 mit
mit
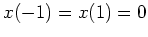 ist.
ist.