Lösung.

Es sei $ \mbox{$\overline x$}$ ein schwaches (lokales) Minimum des gegebenen Problems. Die Eulersche Differentialgleichung liefert $ \mbox{$\ddot{\overline x} \equiv \overline x$}$ auf $ \mbox{$\left[0,\overline b\right]$}$ , d.h. es ist $ \mbox{$\overline x(t) = c \sinh t + d \cosh t$}$ , $ \mbox{$c, d \in \mathbb{R}$}$ , $ \mbox{$t \in \left[0,\overline b\right]$}$ .

Mit $ \mbox{$\overline{x}(0)=0$}$ folgt unmittelbar $ \mbox{$d=0$}$ , d.h. es ist $ \mbox{$\overline{x}(t) = c \sinh t$}$ . Ferner folgt mit der rechten Randbedingung $ \mbox{$x(\overline b)=c \sinh \overline b=\cosh \overline b$}$ . Schließlich liefert die Transversalitätsbedingung

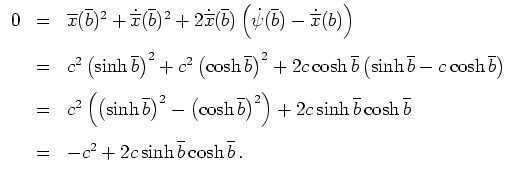
$ \mbox{$\displaystyle \begin{array}{rcl} 0 &=& \overline x(\overline b)^2 +... ...3mm}\\ &=& -c^2 + 2c \sinh \overline b \cosh \overline b\,. \end{array} $}$
Das Gleichungssystem
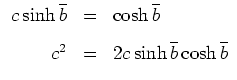
$ \mbox{$\displaystyle \begin{array}{rcl} c \sinh \overline b &=& \cosh \over... ...space{3mm}\\ c^2 &=& 2c \sinh \overline b \cosh \overline b \end{array} $}$
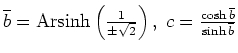besitzt die Lösungen $ \mbox{$\overline b = \text{Arsinh} \left(\frac{1}{\pm \sqrt 2}\right), \; c = \frac{\cosh \overline b}{\sinh \overline b}$}$ . Da wir $ \mbox{$b > 0$}$ vorausgesetzt haben, ist also
$ \mbox{$\displaystyle \overline x(t) = \sqrt 2 \cosh\left( \text{Arsinh} \lef... ... \; t \in \left[0, \text{Arsinh} \left(\tfrac{1}{ \sqrt 2}\right) \right], $}$
der einzige Kandidat für ein schwaches (lokales) Minimum.