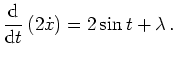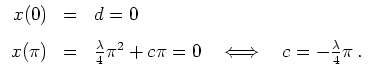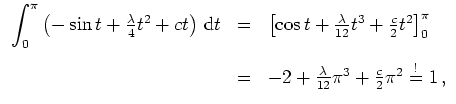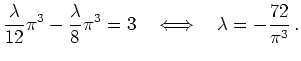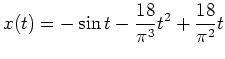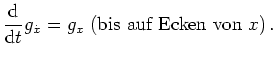Wir definieren
und erhalten mit der Eulerschen Differentialgleichung für
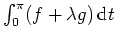 Beachte, daß ein schwaches (lokales) Minimum von
Beachte, daß ein schwaches (lokales) Minimum von
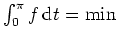 demnach keine Ecke besitzt, daß also die obige Gleichung auf dem gesamten Intervall
demnach keine Ecke besitzt, daß also die obige Gleichung auf dem gesamten Intervall
![$ \mbox{$[0,\pi]$}$](img5.png) gilt. Folglich ist
also
mit noch zu bestimmenden Konstanten
gilt. Folglich ist
also
mit noch zu bestimmenden Konstanten
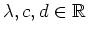 ,
,
![$ \mbox{$t \in [0,\pi]\,$}$](img9.png) . Aufgrund der Randbedingungen folgt
Die Nebenbedingung liefert
also die Gleichung
Hieraus erhalten wir
. Aufgrund der Randbedingungen folgt
Die Nebenbedingung liefert
also die Gleichung
Hieraus erhalten wir
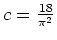 und den Kandidaten
für ein schwaches (lokales) Minimum des gegebenen Variationsproblems, der die Randbedingungen und Nebenbedingungen erfüllt. Um alle Kandidaten für ein schwaches (lokales) Minimum des Problems zu erhalten, betrachten wir noch die Eulersche Differentialgleichung für die Nebenbedingung, also
Diese Bedingung erfüllt jedoch kein
und den Kandidaten
für ein schwaches (lokales) Minimum des gegebenen Variationsproblems, der die Randbedingungen und Nebenbedingungen erfüllt. Um alle Kandidaten für ein schwaches (lokales) Minimum des Problems zu erhalten, betrachten wir noch die Eulersche Differentialgleichung für die Nebenbedingung, also
Diese Bedingung erfüllt jedoch kein
![$ \mbox{$x\in C^1_s[0,\pi]\,$}$](img16.png) , sodaß es keinen weiteren Kandidaten für ein schwaches (lokales) Minimum des Variationsproblems gibt.
, sodaß es keinen weiteren Kandidaten für ein schwaches (lokales) Minimum des Variationsproblems gibt.