Natürliche Randbedingungen.
Es sei das Variationsproblem
ohne Randbedingungen gegeben (d.h. mit
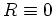 ). Ist nun
). Ist nun
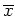 ein schwaches (lokales) Minimum von
ein schwaches (lokales) Minimum von
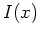 , so gelten die natürlichen Randbedingungen
Ist
, so gelten die natürlichen Randbedingungen
Ist
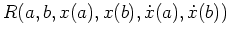 lediglich unabhängig von
lediglich unabhängig von
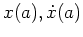 bzw. von
bzw. von
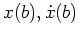 , so gilt entsprechend nur eine der natürlichen Randbedingungen.
, so gilt entsprechend nur eine der natürlichen Randbedingungen.
Transversalitätsbedingungen.
Wir betrachten hier das Variationsproblem
mit ,,freien`` Endpunkten
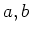 ,
,
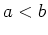 .
Die Randbedingungen dieses Problems sind gegeben durch
.
Die Randbedingungen dieses Problems sind gegeben durch
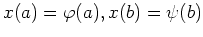 mit Funktionen
mit Funktionen
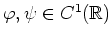 .
.
Ein schwaches (lokales) Minimum dieses Problems ist eine Funktion
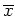 , für die gilt:
, für die gilt:
![$ \mbox{$\overline x \in C^1_s[\overline a,\overline b], \; \overline a < \overl...
...ne a) = \varphi(\overline a), \; \overline x(\overline b) = \psi(\overline b)$}$](img14.png) und es gibt ein
und es gibt ein
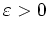 so, daß
so, daß
für alle
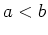 und zulässigen
und zulässigen
 mit
mit
- (i)
-
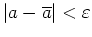 ,
,
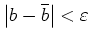 .
.
- (ii)
-
![$ \mbox{$\sup\limits_{[a,b] \cap \left[\overline a,\overline b\right]} \{ \vert ...
...rline x(t)\vert + \vert\dot x(t) - \dot{\overline x}(t)\vert \} < \varepsilon$}$](img20.png) .
.
- (iii)
-
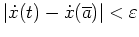 für alle
für alle
![$ \mbox{$t \in [a,\overline a]$}$](img22.png) , falls
, falls
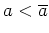 ,
,
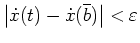 für alle
für alle
![$ \mbox{$t \in \left[\overline b,b\right]$}$](img25.png) , falls
, falls
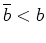 .
.
Dabei heißt
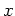 zulässig, falls
zulässig, falls
![$ \mbox{$x \in C_s^1[a,b]$}$](img27.png) und
und
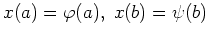 gilt.
gilt.
Ist
![$ \mbox{$\overline x:\left[\overline a,\overline b\right]$}$](img29.png) ein schwaches (lokales) Minimum dieses Problems, so gelten
ein schwaches (lokales) Minimum dieses Problems, so gelten
- (i)
- die Eulersche Differentialgleichung
auf
![$ \mbox{$\left[\overline a,\overline b\right]$}$](img31.png) bis auf die Ecken von
bis auf die Ecken von
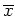 und
und
- (ii)
- die Transversalitätsbedingungen
Bei Randbedingungen der Form
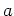 fest,
fest,
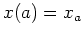 ,
,
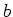 ,,frei``,
,,frei``,
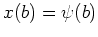 , gilt nur die Transversalitätsbedingung bei
, gilt nur die Transversalitätsbedingung bei
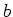 ; falls
; falls
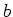 fest,
fest,
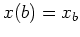 ,
,
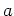 ,,frei`` ist,
,,frei`` ist,
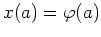 , so gilt entsprechend nur die Transversalitätsbedingung bei
, so gilt entsprechend nur die Transversalitätsbedingung bei
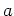 .
.
Die beiden Transversalitätsbedingungen sind also zwei weitere Gleichungen zur Bestimmung der beiden zusätzlichen freien Parameter
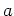 und
und
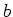 .
.
Isoperimetrische Probleme.
Unter einem isoperimetrischem Problem versteht man ein Variationsproblem
mit einer Nebenbedingung der Form
Dabei seien
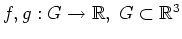 ein Gebiet, und es gelte
ein Gebiet, und es gelte
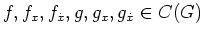 . Weiterhin schreiben wir
. Weiterhin schreiben wir
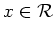 für eine zulässige Funktion
für eine zulässige Funktion
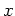 , die die Randbedingungen
, die die Randbedingungen
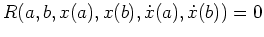 mit einer gegebenen Funktion
mit einer gegebenen Funktion
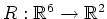 erfüllt.
erfüllt.
Es sei nun
![$ \mbox{$\overline x \in C^1_s[a,b]$}$](img46.png) ein schwaches (lokales) Minimum von
ein schwaches (lokales) Minimum von
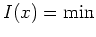 unter der Nebenbedingung
unter der Nebenbedingung
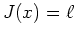 und
und
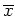 erfülle nicht die zu
erfülle nicht die zu
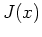 zugehörige Eulersche Differentialgleichung, d.h.
zugehörige Eulersche Differentialgleichung, d.h.
für ein
![$ \mbox{$t \in [a,b]$}$](img51.png) , das keine Ecke von
, das keine Ecke von
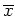 ist. Dann
existiert ein
ist. Dann
existiert ein
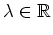 so, daß
so, daß
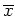 die zu
die zu
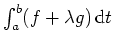 zugehörige
Eulersche Differentialgleichung erfüllt, d.h.
für alle
zugehörige
Eulersche Differentialgleichung erfüllt, d.h.
für alle
![$ \mbox{$t \in [a,b]$}$](img51.png) bis auf Ecken von
bis auf Ecken von
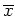 .
.
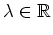 heißt dabei der Lagrange-Parameter und
heißt dabei der Lagrange-Parameter und
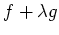 die Lagrange-Funktion.
die Lagrange-Funktion.
Kandidaten für ein schwaches (lokales) Minimum des isoperimetrischen Problems sind also zulässige Funktionen
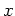 , die entweder die Eulersche Differentialgleichung für
, die entweder die Eulersche Differentialgleichung für
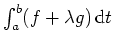 oder die Eulersche Differentialgleichung für
oder die Eulersche Differentialgleichung für
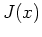 (jeweils bis auf Ecken) und die Neben- und Randbedingungen erfüllen.
(jeweils bis auf Ecken) und die Neben- und Randbedingungen erfüllen.
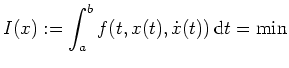
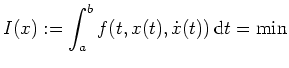
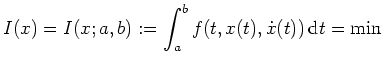
![]() , für die gilt:
, für die gilt:
![]() und es gibt ein
und es gibt ein
![]() so, daß
so, daß
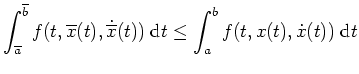
![$ \mbox{$\sup\limits_{[a,b] \cap \left[\overline a,\overline b\right]} \{ \vert ...
...rline x(t)\vert + \vert\dot x(t) - \dot{\overline x}(t)\vert \} < \varepsilon$}$](img20.png) .
.
![]() ein schwaches (lokales) Minimum dieses Problems, so gelten
ein schwaches (lokales) Minimum dieses Problems, so gelten
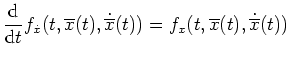
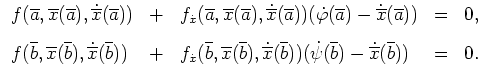
![]() und
und
![]() .
.
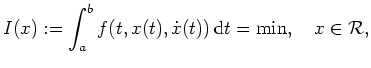
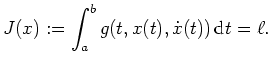
![]() ein schwaches (lokales) Minimum von
ein schwaches (lokales) Minimum von
![]() unter der Nebenbedingung
unter der Nebenbedingung
![]() und
und
![]() erfülle nicht die zu
erfülle nicht die zu
![]() zugehörige Eulersche Differentialgleichung, d.h.
zugehörige Eulersche Differentialgleichung, d.h.
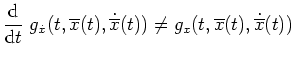
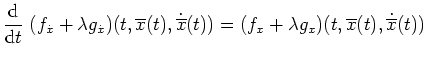
![]() , die entweder die Eulersche Differentialgleichung für
, die entweder die Eulersche Differentialgleichung für
![]() oder die Eulersche Differentialgleichung für
oder die Eulersche Differentialgleichung für
![]() (jeweils bis auf Ecken) und die Neben- und Randbedingungen erfüllen.
(jeweils bis auf Ecken) und die Neben- und Randbedingungen erfüllen.