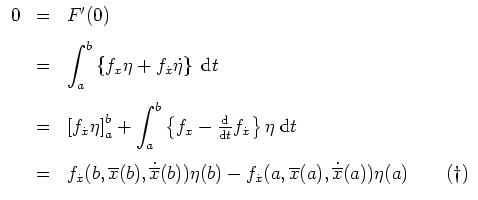Wir bemerken zunächst, daß die Einschränkung
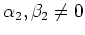 notwendig ist. Es sei etwa das
Variationsproblem
notwendig ist. Es sei etwa das
Variationsproblem
gegeben. Dann ist jede Funktion
![$ \mbox{$x \in C^1_s[0,1]$}$](img3.png) ein schwaches (lokales) Minimum von
ein schwaches (lokales) Minimum von
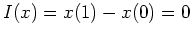 ,
jedoch würde die natürliche Randbedingung für jedes solche
,
jedoch würde die natürliche Randbedingung für jedes solche
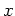 zu einem Widerspruch führen.
zu einem Widerspruch führen.
Wir argumentieren wie bei der ersten Variation. Hierbei addieren wir zu dem schwachen (lokalen) Minimum
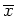 das
das
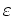 -fache einer zulässigen Variation
-fache einer zulässigen Variation
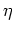 , d.h.
, d.h.
![$ \mbox{$\eta \in C^1[a,b]$}$](img9.png) mit
mit
Ferner sei
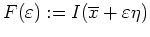 .
Dann besitzt
.
Dann besitzt
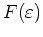 für
für
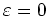 ein lokales Minimum. Daher ist mit partieller Integration und
der Eulerschen
Differentialgleichung
Da
ein lokales Minimum. Daher ist mit partieller Integration und
der Eulerschen
Differentialgleichung
Da
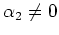 ist, vermögen wir mittels der Hermite-Interpolation auf ein Polynom
ist, vermögen wir mittels der Hermite-Interpolation auf ein Polynom
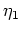 zu
schließen, für das gilt:
Dann ist
zu
schließen, für das gilt:
Dann ist
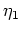 eine zulässige Variation und mit
eine zulässige Variation und mit
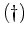 folgt
Analog schließen wir mit
folgt
Analog schließen wir mit
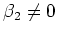 auf ein Polynom
auf ein Polynom
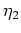 , für das gilt:
Dann ist
, für das gilt:
Dann ist
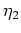 eine zulässige Variation und mit
eine zulässige Variation und mit
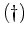 folgt
folgt
![]() notwendig ist. Es sei etwa das
Variationsproblem
notwendig ist. Es sei etwa das
Variationsproblem
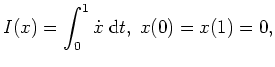
![]() das
das
![]() -fache einer zulässigen Variation
-fache einer zulässigen Variation
![]() , d.h.
, d.h.
![]() mit
mit