Es sei
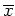 ein schwaches (lokales) Minimum des gegebenen Variationsproblems und es sei
ein schwaches (lokales) Minimum des gegebenen Variationsproblems und es sei
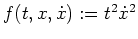 . Aufgrund der 1. Weierstraß-Erdmannschen Eckenbedingung besitzt
. Aufgrund der 1. Weierstraß-Erdmannschen Eckenbedingung besitzt
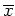 höchstens im Punkt
höchstens im Punkt
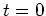 eine
Ecke. Die Eulersche Differentialgleichung liefert
eine
Ecke. Die Eulersche Differentialgleichung liefert
auf
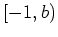 (bzw. falls
(bzw. falls
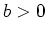 auf
auf
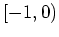 und auf
und auf
![$ \mbox{$(0,b]$}$](img8.png) ). Es ist also
auf
). Es ist also
auf
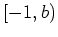 (bzw. falls
(bzw. falls
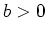 auf
auf
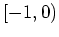 und auf
und auf
![$ \mbox{$(0,b]$}$](img8.png) ). Damit ist
mit gewissen Konstanten
). Damit ist
mit gewissen Konstanten
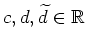 .
Da das schwache (lokale) Minimum
.
Da das schwache (lokale) Minimum
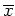 jedoch auf ganz
jedoch auf ganz
![$ \mbox{$[-1,b]$}$](img12.png) existiert und stetig ist,
muß
existiert und stetig ist,
muß
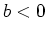 gelten.
gelten.
Die Randbedingungen lauten
Die Transversalitätsbedingung liefert
Diese Gleichung vereinfacht sich zu
d.h. es ist
Mit
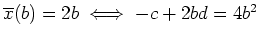 ergibt sich mit obiger Gleichung
Diese Gleichung besitzt die Lösungen
Da
ergibt sich mit obiger Gleichung
Diese Gleichung besitzt die Lösungen
Da
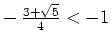 ist, fällt diese Lösung weg. Somit erhalten wir die beiden möglichen
Kandidaten für ein schwaches (lokales) Minimum von
ist, fällt diese Lösung weg. Somit erhalten wir die beiden möglichen
Kandidaten für ein schwaches (lokales) Minimum von
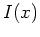 Es ist
Es ist
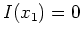 und
und
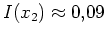 . Da
. Da
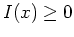 für alle zulässigen Funktionen
für alle zulässigen Funktionen
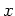 gilt,
ist
gilt,
ist
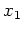 sogar ein globales Minimum von
sogar ein globales Minimum von
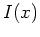 .
.
![]() ein schwaches (lokales) Minimum des gegebenen Variationsproblems und es sei
ein schwaches (lokales) Minimum des gegebenen Variationsproblems und es sei
![]() . Aufgrund der 1. Weierstraß-Erdmannschen Eckenbedingung besitzt
. Aufgrund der 1. Weierstraß-Erdmannschen Eckenbedingung besitzt
![]() höchstens im Punkt
höchstens im Punkt
![]() eine
Ecke. Die Eulersche Differentialgleichung liefert
eine
Ecke. Die Eulersche Differentialgleichung liefert
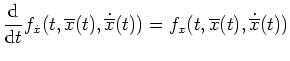
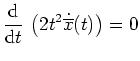
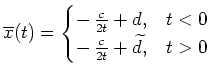
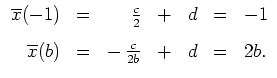
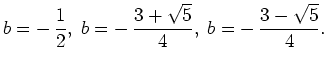
![$ \mbox{$\displaystyle
\begin{array}{rcl}
x_1(t) &=& -1 \text{ auf } [-1,-\...
...5)}{1+\sqrt 5}
\text{ auf } [-1,- \, \frac{3-\sqrt 5}{4}].
\end{array}
$}$](img23.png)