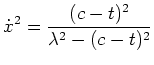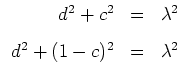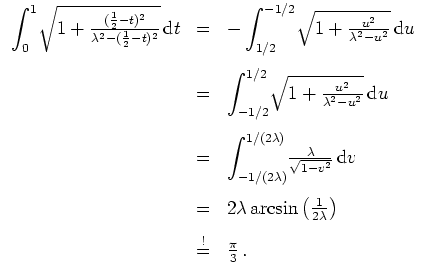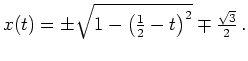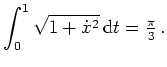Wir definieren
Die Eulersche Differentialgleichung für
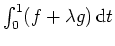 liefert
auf
liefert
auf
![$ \mbox{$[0,1]$}$](img4.png) für ein
für ein
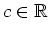 . Daraus ergibt sich
und somit
. Daraus ergibt sich
und somit
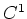 -Kandidaten für ein schwaches (lokales) Minimum des Variationsproblems sind also gewisse Kreisbögen. Aus den Nebenbedingungen erhalten wir
und daraus
-Kandidaten für ein schwaches (lokales) Minimum des Variationsproblems sind also gewisse Kreisbögen. Aus den Nebenbedingungen erhalten wir
und daraus
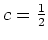 sowie die Gleichung
sowie die Gleichung
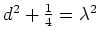 . Ferner liefert die Nebenbedingung
Man überlegt sich, daß die einzigen Lösungen dieser Gleichung
. Ferner liefert die Nebenbedingung
Man überlegt sich, daß die einzigen Lösungen dieser Gleichung
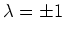 sind. Damit folgt
sind. Damit folgt
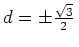 und wir erhalten die zwei Kandidaten
Diese Kandidaten sind (bekanntermaßen) Halbkreise. Wir betrachten nun noch die zur Nebenbedingung zugehörige Eulersche Differentialgleichung. Diese liefert
auf
und wir erhalten die zwei Kandidaten
Diese Kandidaten sind (bekanntermaßen) Halbkreise. Wir betrachten nun noch die zur Nebenbedingung zugehörige Eulersche Differentialgleichung. Diese liefert
auf
![$ \mbox{$[0,1]$}$](img4.png) . Die allgemeine Lösung jener Differentialgleichung lautet
mit Konstanten
. Die allgemeine Lösung jener Differentialgleichung lautet
mit Konstanten
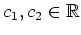 . Die Randbedingungen des vorliegenden Variationsproblems führen auf die
Gleichungen
d.h. es ist
. Die Randbedingungen des vorliegenden Variationsproblems führen auf die
Gleichungen
d.h. es ist
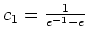 und
und
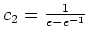 . Die eindeutige Lösung der Eulerschen
Differentialgleichung
erfüllt jedoch nicht die Nebenbedingung
Es kommen also durch die Betrachtung der zur Nebenbedingung zugehörigen Eulerschen Differentialgleichung keine weiteren Kandidaten für ein schwaches (lokales) Minimum des vorliegenden Variationsproblems hinzu.
. Die eindeutige Lösung der Eulerschen
Differentialgleichung
erfüllt jedoch nicht die Nebenbedingung
Es kommen also durch die Betrachtung der zur Nebenbedingung zugehörigen Eulerschen Differentialgleichung keine weiteren Kandidaten für ein schwaches (lokales) Minimum des vorliegenden Variationsproblems hinzu.