Lösung.

Da wir lediglich an stetig differenzierbare Minima 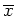$ \mbox{$\overline x$}$ des gegebenen Variationsproblems interessiert sind, betrachten wir Lösungen der Eulersche Differentialgleichung

$ \mbox{$\displaystyle \cos \dot{x}(t) \equiv \text{const.} $}$
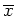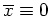auf dem gesamten Intervall $ \mbox{$[0,\pi]$}$ . Folglich ist $ \mbox{$\overline x$}$ linear und im Hinblick auf die Randbedingungen identisch Null auf $ \mbox{$[0,\pi]$}$ . Die Weierstraß'sche Exzess-Funktion liefert für $ \mbox{$\overline x \equiv 0$}$
$ \mbox{$\displaystyle E(t,\overline x(t), \dot{\overline x}(t), w) = \sin w - w, \quad (t,w) \in [0,\pi]\times\mathbb{R}. $}$
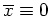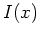Da diese Funktion negative Werte annehmen kann, ist $ \mbox{$\overline x \equiv 0$}$ kein starkes (lokales) Minimum von $ \mbox{$I(x)$}$ .