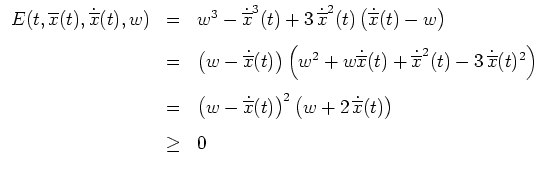
Nach der Eulerschen Differentialgleichung ist
![]() auf
auf
![]() , so daß ein schwaches (lokales)
Minimum von
, so daß ein schwaches (lokales)
Minimum von
![]() linear auf
linear auf
![]() ist. Im Hinblick auf die Randbedingungen erhalten wir somit den einzigen Kandidaten
ist. Im Hinblick auf die Randbedingungen erhalten wir somit den einzigen Kandidaten
![]() für
für
![]() .
.
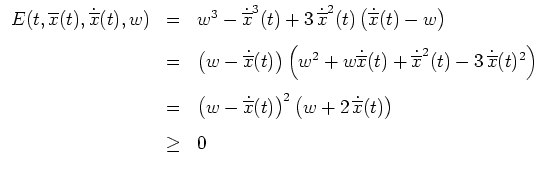
Nach der Eulerschen Differentialgleichung ist
![]() auf
auf
![]() , so daß ein schwaches (lokales)
Minimum von
, so daß ein schwaches (lokales)
Minimum von
![]() linear auf
linear auf
![]() ist. Im Hinblick auf die Randbedingungen erhalten wir somit den einzigen Kandidaten
ist. Im Hinblick auf die Randbedingungen erhalten wir somit den einzigen Kandidaten
![]() für
für
![]() .
.