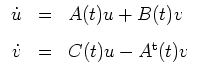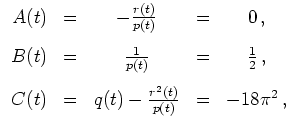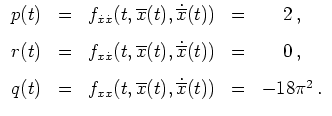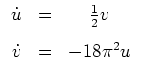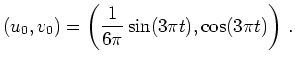Die Eulersche Differentialgleichung liefert die inhomogene lineare Differentialgleichung zweiter Ordnung
auf
![$ \mbox{$[0,\frac{1}{2}]$}$](img2.png) . Die allgemeine Lösung dieser Differentialgleichung lautet
mit beliebigen Konstanten
. Die allgemeine Lösung dieser Differentialgleichung lautet
mit beliebigen Konstanten
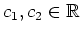 . Im Hinblick auf die Randbedingungen erhalten wir somit den eindeutigen Kandidaten
für ein schwaches (lokales) Minimum des gegebenen Variationsproblems. Da ferner die verschärfte
Legendre-Bedingung
. Im Hinblick auf die Randbedingungen erhalten wir somit den eindeutigen Kandidaten
für ein schwaches (lokales) Minimum des gegebenen Variationsproblems. Da ferner die verschärfte
Legendre-Bedingung
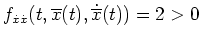 auf
auf
![$ \mbox{$[0,\frac{1}{2}]$}$](img2.png) erfüllt ist,
berechnen wir die Hauptlösung des zugehörigen Hamiltonschen Systems
mit
wobei
Das Hamiltonsche System
führt uns auf die homogene lineare Differentialgleichung zweiter Ordnung
Die Hauptlösung
erfüllt ist,
berechnen wir die Hauptlösung des zugehörigen Hamiltonschen Systems
mit
wobei
Das Hamiltonsche System
führt uns auf die homogene lineare Differentialgleichung zweiter Ordnung
Die Hauptlösung
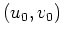 dieses Hamiltonschen Systems, d.h. die Lösung des Systems zu den Anfangswerten
dieses Hamiltonschen Systems, d.h. die Lösung des Systems zu den Anfangswerten
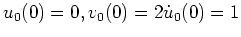 , lautet
Da
, lautet
Da
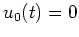 für
für
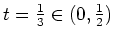 gilt, ist die notwendige Bedingung von Jacobi verletzt.
gilt, ist die notwendige Bedingung von Jacobi verletzt.
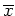 ist somit kein schwaches (lokales) Minimum.
ist somit kein schwaches (lokales) Minimum.