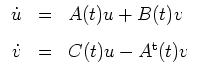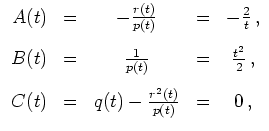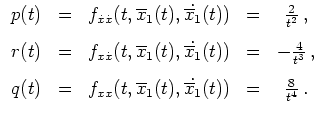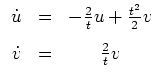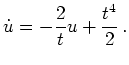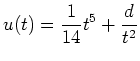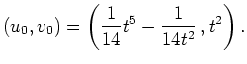Zunächst sei bemerkt, daß zulässige Funktionen
 des Variationsproblems aufgrund des Integranden von
des Variationsproblems aufgrund des Integranden von
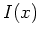 keine
Nullstellen besitzen. Die Randbedingungen implizieren somit, daß
keine
Nullstellen besitzen. Die Randbedingungen implizieren somit, daß
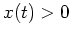 für alle
für alle
![$ \mbox{$t \in [0,1]$}$](img4.png) gilt.
gilt.
- Es sei
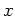 eine zulässige Funktion des gegebenen Variationsproblems, die die Eulersche Differentialgleichung
erfüllt, d.h. es ist
Wir erkennen, daß die rechte Seite dieser Gleichung stetig auf
eine zulässige Funktion des gegebenen Variationsproblems, die die Eulersche Differentialgleichung
erfüllt, d.h. es ist
Wir erkennen, daß die rechte Seite dieser Gleichung stetig auf
![$ \mbox{$[1,2]$}$](img6.png) ist. Da
ist. Da
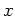 als zulässige Funktion ebenfalls
stetig auf
als zulässige Funktion ebenfalls
stetig auf
![$ \mbox{$[1,2]$}$](img6.png) ist, folgt auch, daß
ist, folgt auch, daß
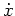 stetig auf
stetig auf
![$ \mbox{$[1,2]$}$](img6.png) ist, d.h. es ist
ist, d.h. es ist
![$ \mbox{$x \in C^1[1,2]$}$](img8.png) .
.
Da damit die rechte Seite der Gleichung
differenzierbar ist, erhalten wir aus der Eulerschen Differentialgleichung die implizite Differentialgleichung
zweiter Ordnung
Da
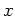 keine Nullstelle besitzt, ist
keine Nullstelle besitzt, ist
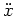 differenzierbar auf
differenzierbar auf
![$ \mbox{$[1,2]$}$](img6.png) und somit
und somit
![$ \mbox{$x \in C^2[1,2]$}$](img12.png) .
Differenzieren wir diese Gleichung, so erhalten wir
Damit ist eine zulässige Funktion
.
Differenzieren wir diese Gleichung, so erhalten wir
Damit ist eine zulässige Funktion
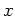 , die die Eulersche Differentialgleichung erfüllt, ein Polynom höchstens
vom Grad
, die die Eulersche Differentialgleichung erfüllt, ein Polynom höchstens
vom Grad
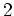 . Also ist
. Also ist
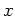 von der Form
mit Konstanten
von der Form
mit Konstanten
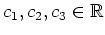 . Setzen wir diesen Ausdruck in die Gleichung
. Setzen wir diesen Ausdruck in die Gleichung
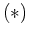 ein, so erhälten wir die folgenden Fälle. Entweder ist
ein, so erhälten wir die folgenden Fälle. Entweder ist
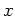 konstant, oder es ist
mit Konstanten
konstant, oder es ist
mit Konstanten
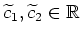 .
.
- Die Lösungen aus Aufgabenteil 1., die die Randbedingungen erfüllen, sind
gegeben durch
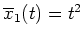 und
und
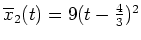 .
.
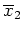 hat aber auf dem Intervall
hat aber auf dem Intervall
![$ \mbox{$[1,2]$}$](img6.png) eine Nullstelle, ist also offensichtlich keine zulässige Funktion für das gegebene Variationsproblem
eine Nullstelle, ist also offensichtlich keine zulässige Funktion für das gegebene Variationsproblem
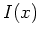 . Demnach beschränken wir unsere weiteren Untersuchungen auf
. Demnach beschränken wir unsere weiteren Untersuchungen auf
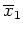 .
.
Die verschärfte Legendre-Bedingung
ist erfüllt, also berechnen wir die Hauptlösung des zugehörigen Hamiltonschen Systems
mit
wobei
Das Hamiltonsche System
führt uns sofort auf
mit einer beliebigen Konstanten
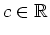 . Im Hinblick auf die Hauptlösung
. Im Hinblick auf die Hauptlösung
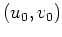 dieses Hamiltonschen Systems, d.h. die Lösung des Systems zu den Anfangswerten
dieses Hamiltonschen Systems, d.h. die Lösung des Systems zu den Anfangswerten
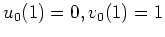 , erhalten wir also
, erhalten wir also
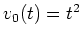 und die lineare Differentialgleichung erster Ordnung
Die Lösungen dieser Differentialgleichung sind von der Gestalt
mit einer beliebigen Konstanten
und die lineare Differentialgleichung erster Ordnung
Die Lösungen dieser Differentialgleichung sind von der Gestalt
mit einer beliebigen Konstanten
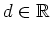 . Also ist die Hauptlösung des Hamiltonschen Systems gegeben durch
Da
. Also ist die Hauptlösung des Hamiltonschen Systems gegeben durch
Da
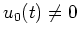 auf
auf
![$ \mbox{$(1,2]$}$](img39.png) gilt, folgt aus der hinreichenden Bedingung von Jacobi-Legendre, daß
gilt, folgt aus der hinreichenden Bedingung von Jacobi-Legendre, daß
 ein schwaches (lokales) Minimum ist.
ein schwaches (lokales) Minimum ist.
![]() des Variationsproblems aufgrund des Integranden von
des Variationsproblems aufgrund des Integranden von
![]() keine
Nullstellen besitzen. Die Randbedingungen implizieren somit, daß
keine
Nullstellen besitzen. Die Randbedingungen implizieren somit, daß
![]() für alle
für alle
![]() gilt.
gilt.
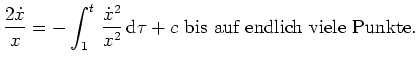
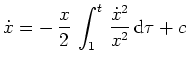
![$ \mbox{$\displaystyle
f_{\dot x\dot x}(t,\overline x_1(t), \dot{\overline x_1}(t)) = \frac{2}{\overline x_1(t)} > 0 \quad\text{auf }[1,2]
$}$](img24.png)