Repetitorium Variationsrechnung

Die Theorie der 2. Variation.

Die 2. Variation.

Es sei $\mbox{$x_0\in C_s^1[a,b]$}$ eine zulässige Funktion für das Variationsproblem

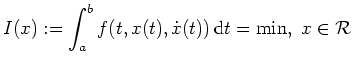
$\mbox{$\displaystyle I(x) := \int_a^b f(t,x(t),\dot x(t)) \, \text{d}t = \min, \; x \in \mathcal{R} $}$

(d.h. es ist $\mbox{$R(a,b,x(a),x(b),\dot x(a),\dot x(b))=0$}$ für eine gegebene Funktion $\mbox{$R:\mathbb{R}^6 \to \mathbb{R}^2$}$ ), und es sei $\mbox{$\eta \in C_s^1[a,b]$}$ eine zulässige Variation für das obige Variationsproblem. Zusätzlich zu den üblichen Voraussetzungen seien $\mbox{$f,f_x,f_{\dot x}, f_{xx}, f_{x\dot x}, f_{\dot x\dot x} \in C(G)$}$ , $\mbox{$G \subset \mathbb{R}^3$}$ ein Gebiet.

Dann ist die Funktion $\mbox{$F(\varepsilon) := I(x_0+\varepsilon \eta)$}$ für $\mbox{$\vert\varepsilon\vert \leq \varepsilon_0$}$ , $\mbox{$\varepsilon_0 > 0$}$ hinreichend klein, wohldefiniert und zweimal stetig differenzierbar auf $\mbox{$(-\varepsilon_0, \varepsilon_0)$}$ . Es gilt

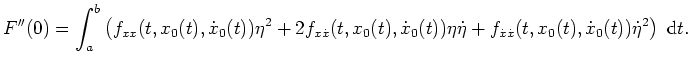
$\mbox{$\displaystyle F''(0) = \int_a^b \left( f_{xx}(t,x_0(t),\dot x_0(t)) \... ...+ f_{\dot x \dot x}(t,x_0(t),\dot x_0(t)) \dot \eta^2 \right) \; \text{d}t. $}$

Diese Größe heißt die 2. (Gâteaux-) Variation von $\mbox{$I(x)$}$ bei $\mbox{$x=x_0$}$ in Richtung $\mbox{$\eta$}$ . Wir schreiben $\mbox{$I''(x_0,\eta)$}$ oder $\mbox{$\partial^2 I(x_0,\eta)$}$ .

Ist nun $\mbox{$\overline x$}$ ein schwaches (lokales) Minimum für $\mbox{$I(x)=\min$}$ , $\mbox{$x \in \mathcal{R}$}$ , so gilt $\mbox{$I''(\overline x,\eta) = \partial^2 I(\overline x,\eta) \geq 0$}$ für alle zulässigen Variationen $\mbox{$\eta$}$ .

Da diese Bedingung jedoch $\mbox{$\eta$}$ enthält, ist sie ebenso wie die 1. (Gâteaux-)Variation nicht sehr praktikabel. Wir suchen daher eine Bedingung, die $\mbox{$\eta$}$ nicht mehr enthält. Bei Problemen mit festen Rändern (also $\mbox{$\eta(a)=\eta(b)=0$}$ ) beobachten wir, daß die obige Bedingung auf ein spezielles Variationsproblem, nämlich

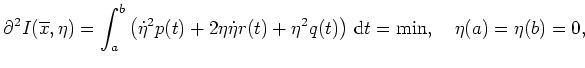
$\mbox{$\displaystyle \partial^2 I(\overline x,\eta) = \int_a^b \left( \dot ... ...t \eta r(t) + \eta^2 q(t) \right)\,\text{d}t=\min, \quad \eta(a)=\eta(b)=0, $}$

mit $\mbox{$p(t):=f_{\dot x \dot x}(t,\overline x(t),\dot{\overline x}(t))$}$ , $\mbox{$r(t):=f_{x \dot x}(t,\overline x(t),\dot{\overline x}(t))$}$ , $\mbox{$q(t):=f_{xx}(t,\overline x(t),\dot{\overline x}(t))$}$ führt.

Es sind $\mbox{$p,r,q\in C[a,b]$}$ . Aufgrund der Legendre-Bedingung gilt $\mbox{$p(t)\geq 0$}$ auf $\mbox{$[a,b]$}$ . Für weitere Untersuchungen setzen wir nun die verschärfte Legendre-Bedingung $\mbox{$p(t) > 0$}$ auf $\mbox{$[a,b]$}$ voraus.

Ferner nennen wir das Funktional $\mbox{$\partial^2 I(\overline x,\eta)$}$

(i): positiv semidefinit, falls $\mbox{$\partial^2 I(\overline x,\eta)\geq 0$}$ für alle zulässigen $\mbox{$\eta\in C^1_s[a,b]$}$ mit $\mbox{$\eta(a)=\eta(b)=0$}$ gilt,
(ii): positiv definit, falls $\mbox{$\partial^2 I(\overline x,\eta)$}$ positiv semidefinit ist und zusätzlich $\mbox{$\partial^2 I(\overline x,\eta)=0\iff \eta\equiv 0\,$}$ auf $\mbox{$[a,b]$}$ gilt.

Mit der Eulerschen Differentialgleichung sowie der 1. Weierstraß-Erdmannschen Eckenbedingung folgt

(i): $\mbox{$p\dot \eta + r\eta \in C[a,b]$}$ und somit $\mbox{$\dot \eta \in C[a,b]$}$ ,
(ii): $\mbox{$\dfrac{\text{d}}{\text{d}t}\left(p(t)\dot \eta + r(t)\eta\right) = r(t)\dot \eta + q(t)\eta\ \text{ auf } [a,b] \quad (*)$}$ .

Nun ist $\mbox{$\eta\in C^1[a,b]$}$ eine Lösung der Eulerschen Differentialgleichung $\mbox{$(*)$}$ genau dann, wenn $\mbox{$u(t):=\eta(t)$}$ und $\mbox{$v(t):=p(t)\dot \eta(t) + r(t)\eta(t)$}$ das lineare Hamiltonsche System

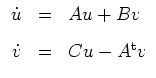
$\mbox{$\displaystyle \begin{array}{rcl} \dot u &=& Au + Bv\vspace{3mm}\\ \dot v &=& Cu - A^\text{t}v \end{array} $}$

mit $\mbox{$A(t)=-p^{-1}(t)r(t)$}$ , $\mbox{$B(t)=p^{-1}(t)$}$ , $\mbox{$C(t)=q(t)-p^{-1}(t)r^2(t)$}$ lösen. Dabei gilt: $\mbox{$A(t),B(t),C(t)\in C[a,b]$}$ und $\mbox{$B(t)>0$}$ auf $\mbox{$[a,b]$}$ .

Die eindeutig bestimme Lösung $\mbox{$(u_0,v_0)$}$ des Hamiltonschen Systems mit dem Anfangswert $\mbox{$u_0(a)=0$}$ und $\mbox{$v_0(a)=1$}$ heißt Hauptlösung des Hamiltonschen Systems bei $\mbox{$a$}$ (kurz: Hauptlösung bei $\mbox{$a$}$ ).

Unter obigen Voraussetzungen ist das quadratische Funktional $\mbox{$\partial^2 I(\overline x,\eta)$}$ genau dann

(i): positiv semidefinit, wenn für die Hauptlösung $\mbox{$(u_0,v_0)$}$ bei $\mbox{$a$}$ gilt: $\mbox{$u_0(t) \neq 0$}$ für alle $\mbox{$t \in (a,b)$}$ .
(ii): positiv definit, wenn für die Hauptlösung $\mbox{$(u_0,v_0)$}$ bei $\mbox{$a$}$ gilt: $\mbox{$u_0(t) \neq 0$}$ für alle $\mbox{$t \in (a,b]$}$ .

Die notwendige Bedingung von Jacobi.

Es gelte $\mbox{$f,f_x,f_{\dot x}, f_{xx}, f_{x\dot x}, f_{\dot x\dot x} \in C(G)$}$ . Weiter sei $\mbox{$\overline x \in C_s^1[a,b]$}$ schwaches (lokales) Minimum von $\mbox{$I(x):= \int_a^b f(t,x(t),\dot x(t)) \, \text{d}t = \min$}$ , $\mbox{$x \in \mathcal{R}$}$ , und es gelte die verschärfte Legendre-Bedingung, d.h.

$\mbox{$\displaystyle p(t) = f_{\dot x \dot x}(t,\overline x(t),\dot{\overline x}(t)) > 0 \text{ f\uml ur alle } t\in[a,b]. $}$

Dann ist $\mbox{$\overline x \in C^1[a,b]$}$ (d.h. $\mbox{$\overline x$}$ hat keine Ecken),

$\mbox{$\displaystyle p(t) = f_{\dot x \dot x}(t,\overline x(t),\dot{\overli... ...verline x}(t)), \quad q(t) =f_{xx}(t,\overline x(t),\dot{\overline x}(t)) $}$

sind stetig auf $\mbox{$[a,b]$}$ , und es gilt die Jacobi-Bedingung, d.h. für die Hauptlösung $\mbox{$(u_0,v_0)$}$ des zugehörigen Hamiltonschen Systems gilt: $\mbox{$u_0(t) \neq 0$}$ für alle $\mbox{$t \in (a,b)$}$ .

Die hinreichende Bedingung von Jacobi-Legendre.

Es sei nun ein Variationsproblem $\mbox{$I(x):= \int_a^b f(t,x(t),\dot x(t)) \, \text{d}t = \min$}$ mit $\mbox{$x(a)=x_1, x(b)=x_2$}$ (d.h. mit festen Rändern) gegeben und $\mbox{$f$}$ erfülle die obigen Voraussetzungen. Ferner erfülle ein $\mbox{$\overline x \in C^1$}$ die folgenden Bedingungen.

$\mbox{$\overline x$}$ ist zulässig.
$\mbox{$\frac{\text{d}}{\text{d}t} \, f_{\dot x}(t,\overline x(t), \dot{\overline x}(t)) = f_x(t,\overline x(t),\dot{\overline x}(t))$}$ für alle $\mbox{$t \in [a,b]$}$ (Eulersche Dgl.).
$\mbox{$p(t) = f_{\dot x \dot x}(t,\overline x(t), \dot{\overline x}(t)) > 0$}$ für alle $\mbox{$t \in [a,b]$}$ (verschärfte Legendre-Bedingung).
Für die Hauptlösung $\mbox{$(u_0,v_0)$}$ des zugehörigen Hamiltonschen Systems gilt: $\mbox{$u_0(t) \neq 0$}$ für alle $\mbox{$t \in (a,b]$}$ . Dies ist die sogenannte verschärfte Jacobi-Bedingung.

Dann ist $\mbox{$\overline x$}$ ein schwaches (lokales) Minimum des obigen Variationsproblems.