Die Eulersche Differentialgleichung liefert
für alle
![$ \mbox{$t \in [1,2]$}$](img2.png) bis auf endlich viele Punkte mit einer Konstanten
bis auf endlich viele Punkte mit einer Konstanten
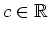 . Da
für alle
. Da
für alle
![$ \mbox{$t \in [1,2]$}$](img2.png) gilt, ist die verschärfte Legendre-Bedingung für jeden Kandidaten eines
schwachen (lokalen) Minimums des gegebenen Variationsproblems erfüllt. Insbesondere besitzt eine zulässige
Lösung der Eulerschen Differentialgleichung keine Ecken.
gilt, ist die verschärfte Legendre-Bedingung für jeden Kandidaten eines
schwachen (lokalen) Minimums des gegebenen Variationsproblems erfüllt. Insbesondere besitzt eine zulässige
Lösung der Eulerschen Differentialgleichung keine Ecken.
Durch Quadrieren der Eulerschen Differentialgleichung erhalten wir die Bedingung
Dieser Gleichung entnehmen wir, daß eine zulässige Funktion, die die Randbedingungen erfüllt, ein
einheitliches Vorzeichen besitzt. Im Hinblick auf die Randbedingungen bedeutet dies
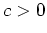 (genauer:
(genauer:
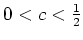 ).
).
Aus der resultierenden Differentialgleichung
erhalten wir unmittelbar durch Integration
mit einer Konstanten
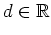 . Die Randbedingungen
. Die Randbedingungen
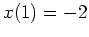 und
und
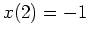 führen auf
führen auf
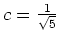 und
und
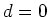 . Somit haben wir einen
eindeutigen Kandidaten für ein schwaches (lokales) Minimum des gegebenen Variationsproblems, nämlich
Ferner ist
Das zugehörige Hamiltonsche System lautet
Die Hauptlösung dieses Systems, d.h. die Lösung
. Somit haben wir einen
eindeutigen Kandidaten für ein schwaches (lokales) Minimum des gegebenen Variationsproblems, nämlich
Ferner ist
Das zugehörige Hamiltonsche System lautet
Die Hauptlösung dieses Systems, d.h. die Lösung
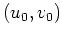 mit
mit
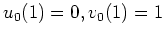 , ist gegeben durch
, ist gegeben durch
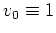 , und der Lösung der Gleichung
, und der Lösung der Gleichung
![$ \mbox{$\dot u_0(t) = t (1 + \dot{\overline x}^2(t))^{3/2} = t\left(\frac{5}{5-t^2}\right)^{3/2}\,, \, t \in [1,2]$}$](img21.png) , mit
, mit
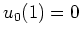 .
.
Demzufolge ist
Da
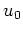 keine Nullstellen auf
keine Nullstellen auf
![$ \mbox{$(1,2]$}$](img25.png) besitzt, folgt aus der hinreichenden Bedingung von Jacobi-Legendre, daß
besitzt, folgt aus der hinreichenden Bedingung von Jacobi-Legendre, daß
 ein schwaches (lokales) Minimum des gegebenen Variationsproblems ist.
ein schwaches (lokales) Minimum des gegebenen Variationsproblems ist.
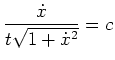
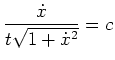
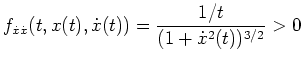
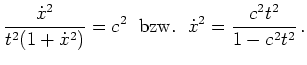
![$ \mbox{$\displaystyle
\dot x = \frac{ct}{\sqrt{1-c^2t^2}}\ \text{ auf } [1,2]
$}$](img8.png)
![$ \mbox{$\displaystyle
x(t) = \frac{- \sqrt{1-c^2 t^2}}{c}\, + d\,, \quad t \in [1,2],
$}$](img9.png)
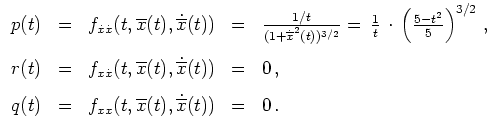
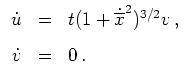
![$ \mbox{$\dot u_0(t) = t (1 + \dot{\overline x}^2(t))^{3/2} = t\left(\frac{5}{5-t^2}\right)^{3/2}\,, \, t \in [1,2]$}$](img21.png) , mit
, mit
![$ \mbox{$\displaystyle
u_0(t) = 5\sqrt 5\left(\frac{1}{\sqrt{5-t^2}}-\frac 1 2\right) > 0 \text{ f\uml ur alle }t\in (1,2].
$}$](img23.png)