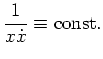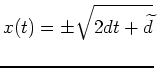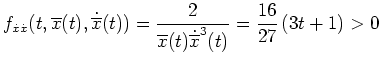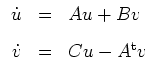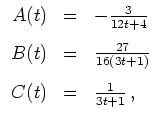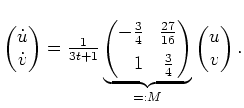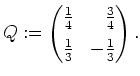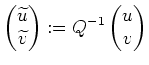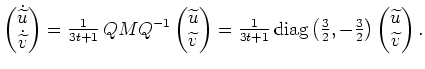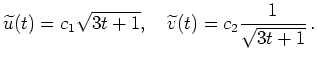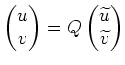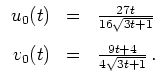Es sei
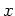 eine Extremale von
eine Extremale von
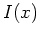 . Dann gilt aufgrund der Eulerschen Differentialgleichung
. Dann gilt aufgrund der Eulerschen Differentialgleichung
mit einer Konstanten
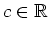 .
Da der Integrand stetig ist, ist die linke Seite jener Gleichung stetig differenzierbar auf
.
Da der Integrand stetig ist, ist die linke Seite jener Gleichung stetig differenzierbar auf
![$ \mbox{$[0,1]$}$](img5.png) .
Damit ist zunächst
.
Damit ist zunächst
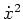 stetig differenzierbar. Da
stetig differenzierbar. Da
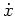 jedoch im Nenner des Integranden von
jedoch im Nenner des Integranden von
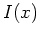 steht
und nach Voraussetzung stetig ist, besitzt
steht
und nach Voraussetzung stetig ist, besitzt
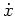 ein einheitliches Vorzeichen. Folglich ist auch
ein einheitliches Vorzeichen. Folglich ist auch
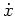 stetig differenzierbar.
Damit ist also
stetig differenzierbar.
Damit ist also
![$ \mbox{$x \in C^2[0,1]$}$](img8.png) .
.
Es bezeichne
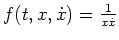 den Integranden von
den Integranden von
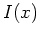 . Wegen
. Wegen
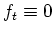 ist
ist
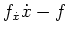 konstant, also folgt
konstant, also folgt
Daraus ergibt sich die Differentialgleichung
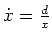 mit einer Konstanten
mit einer Konstanten
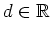 .
Diese besitzt die allgemeine Lösung
mit einer beliebigen Konstanten
.
Diese besitzt die allgemeine Lösung
mit einer beliebigen Konstanten
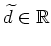 . Im Hinblick auf die Randbedingungen erhalten wir den eindeutigen
Kandidaten
für ein schwaches (lokales) Minimum von
. Im Hinblick auf die Randbedingungen erhalten wir den eindeutigen
Kandidaten
für ein schwaches (lokales) Minimum von
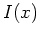 . Da die verschärfte Legendre-Bedingung
auf
. Da die verschärfte Legendre-Bedingung
auf
![$ \mbox{$[0,1]$}$](img5.png) erfüllt ist, untersuchen wir das Hamiltonsche System
mit
d.h.
Wir diagonalisieren die (konstante) Matrix
erfüllt ist, untersuchen wir das Hamiltonsche System
mit
d.h.
Wir diagonalisieren die (konstante) Matrix
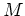 und erhalten
mit
Wir substituieren
und erhalten somit das Differentialgleichungssystem
Wir erhalten die allgemeine Lösung
Mittels der Resubstitution
und im Hinblick auf die Hauptlösung des vorliegenden Hamiltonschen Systems erhalten wir
Da
und erhalten
mit
Wir substituieren
und erhalten somit das Differentialgleichungssystem
Wir erhalten die allgemeine Lösung
Mittels der Resubstitution
und im Hinblick auf die Hauptlösung des vorliegenden Hamiltonschen Systems erhalten wir
Da
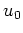 keine Nullstelle auf dem Intervall
keine Nullstelle auf dem Intervall
![$ \mbox{$(0,1]$}$](img31.png) besitzt, ist
besitzt, ist
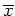 gemäß der hinreichenden Bedingung
von Jacobi-Legendre ein schwaches (lokales) Minimum von
gemäß der hinreichenden Bedingung
von Jacobi-Legendre ein schwaches (lokales) Minimum von
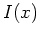 .
.
![]() eine Extremale von
eine Extremale von
![]() . Dann gilt aufgrund der Eulerschen Differentialgleichung
. Dann gilt aufgrund der Eulerschen Differentialgleichung
![$ \mbox{$\displaystyle
- \, \frac{1}{x \dot x^2}
= - \int_0^t \, \frac{1}{x^2 \dot x} \, \text{d} \tau + c, \quad t \in [0,1],
$}$](img3.png)
![]() den Integranden von
den Integranden von
![]() . Wegen
. Wegen
![]() ist
ist
![]() konstant, also folgt
konstant, also folgt