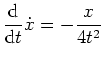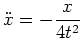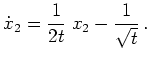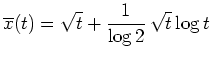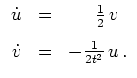Für den Integranden
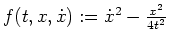 des gegebenen Variatonsproblems gilt
des gegebenen Variatonsproblems gilt
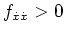 , also hat jedes schwache (lokale) Minimum keine Ecken und erfüllt die Eulersche Differentialgleichung
, also hat jedes schwache (lokale) Minimum keine Ecken und erfüllt die Eulersche Differentialgleichung
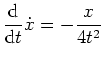
auf
![$ \mbox{$[1,4]$}$](img4.png) . Daraus ergibt sich, daß ein schwaches (lokales) Minimum zweimal stetig differenzierbar ist.
. Daraus ergibt sich, daß ein schwaches (lokales) Minimum zweimal stetig differenzierbar ist.
- In der resultierenden Differentialgleichung
setzen wir
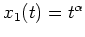 ein und erhalten
Es ist
ein und erhalten
Es ist
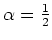 und somit ist
und somit ist
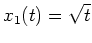 eine Lösung der Eulerschen Differentialgleichung.
eine Lösung der Eulerschen Differentialgleichung.
- Da die Eulersche Differentialgleichung eine lineare Differentialgleichung zweiter Ordnung ist, gibt es zwei
linear unabhängige Lösungen dieser Gleichung. Es bezeichne also
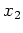 eine zu
eine zu
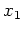 linear unabhängige Lösung.
Da die Eulersche Differentialgleichung nicht explizit den Term
linear unabhängige Lösung.
Da die Eulersche Differentialgleichung nicht explizit den Term
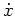 beinhaltet, gilt gemäß der
Wronski-Identität
also
Die Lösungsgesamtheit dieser linearen Differentialgleichung erster Ordnung ist
mit einer beliebigen Konstanten
beinhaltet, gilt gemäß der
Wronski-Identität
also
Die Lösungsgesamtheit dieser linearen Differentialgleichung erster Ordnung ist
mit einer beliebigen Konstanten
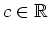 .
Entsprechend ist die Lösungsgesamtheit der Eulerschen Differentialgleichung des gegebenen Variationsproblems
mit Konstanten
.
Entsprechend ist die Lösungsgesamtheit der Eulerschen Differentialgleichung des gegebenen Variationsproblems
mit Konstanten
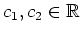 . Im Hinblick auf die Randbedingungen erhalten wir den eindeutigen Kandidaten
für ein schwaches (lokales) Minimum von
. Im Hinblick auf die Randbedingungen erhalten wir den eindeutigen Kandidaten
für ein schwaches (lokales) Minimum von
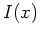 .
.
- Es gilt die verschärfte Legendre-Bedingung, wie wir im Aufgabenteil 1. gesehen haben. Mit
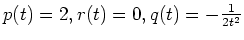 sowie
sowie
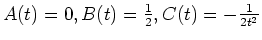 ergibt sich das
zugehörige Hamiltonsche System zu
Es ist also
ergibt sich das
zugehörige Hamiltonsche System zu
Es ist also
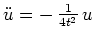 , d.h. analog zu den Aufgabenteilen 1. und 2. ist die allgemeine
Lösung dieser Differentialgleichung gegeben durch
mit Konstanten
, d.h. analog zu den Aufgabenteilen 1. und 2. ist die allgemeine
Lösung dieser Differentialgleichung gegeben durch
mit Konstanten
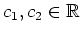 .
Im Hinblick auf die Hauptlösung des Hamiltonschen Systems, d.h. die Lösung
.
Im Hinblick auf die Hauptlösung des Hamiltonschen Systems, d.h. die Lösung
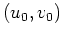 mit
mit
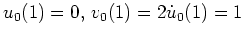 , ergibt sich
Da
, ergibt sich
Da
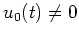 für alle
für alle
![$ \mbox{$t \in (1,4]$}$](img30.png) ist, folgt mit der hinreichenden Bedingung von
Jacobi-Legendre, daß
ist, folgt mit der hinreichenden Bedingung von
Jacobi-Legendre, daß
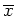 ein schwaches (lokales) Minimum von
ein schwaches (lokales) Minimum von
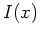 ist.
ist.
![]() des gegebenen Variatonsproblems gilt
des gegebenen Variatonsproblems gilt
![]() , also hat jedes schwache (lokale) Minimum keine Ecken und erfüllt die Eulersche Differentialgleichung
, also hat jedes schwache (lokale) Minimum keine Ecken und erfüllt die Eulersche Differentialgleichung