Jacobi-Verfahren für Randwertprobleme

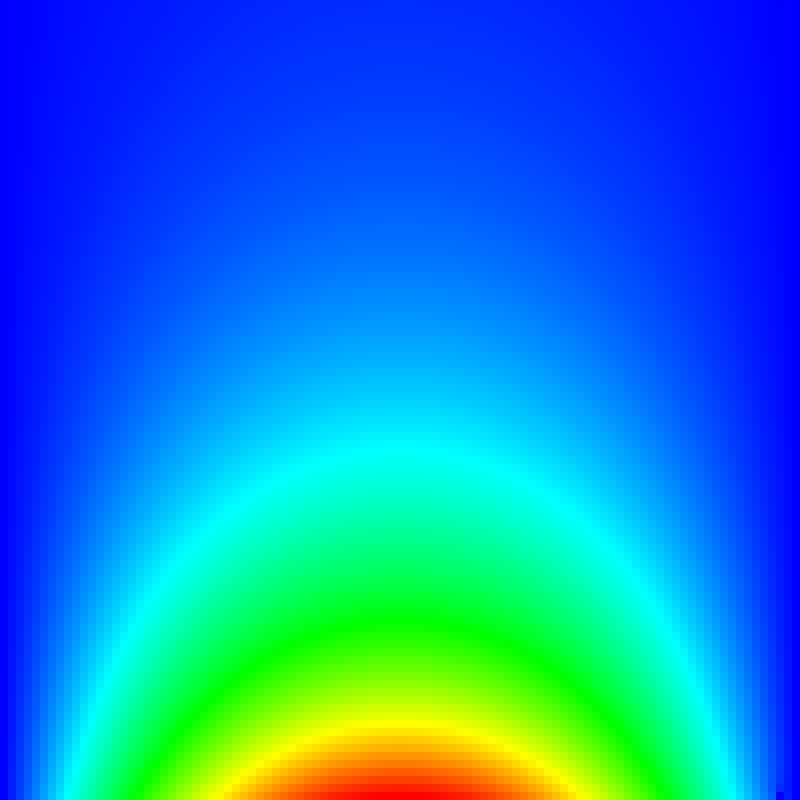
Gesucht sei eine numerische Näherung einer Funktion $u(x,y)$ für $(x, y) \in \Omega = [0,1] \times [0,1]$, für die gilt: $u_{xx} + u_{yy} = 0$ mit der Randbedingung $u(x,y) = g(x,y)$ für $x, y \in \delta\Omega$. Das obige Beispiel zeigt eine numerische Lösung für die Randbedingungen $u(x,0) = sin(\pi x)$, $u(x,1) = sin(\pi x) e^{-\pi}$ und $u(0, y) = u(1, y) = 0$.

Numerisch lässt sich das Problem lösen, wenn das Gebiet $\Omega$ in ein $N \times N$ Gitter gleichmäßig zerlegt wird. Dann lässt sich $u(x,y)$ auf den Gitterpunkten durch eine Matrix $A$ darstellen, wobei $A_{i,j} = u\left(\frac{i}{N}, \frac{j}{N}\right)$ für $i,j = 0 \dots N$:

\[ \left( \begin{array}{ccccc} A_{0,N-1} & A_{1,N-1} & \dots & A_{N-2, N-1} & A_{N-1,N-1} \\ A_{0,N-2} & A_{1,N-2} & \dots & A_{N-2, N-2} & A_{N-1,N-2} \\ \vdots & \vdots & & \vdots & \vdots \\ A_{0,1} & A_{1,1} & \dots & A_{N-2, 1} & A_{N-1, 1} \\ A_{0,0} & A_{1,0} & \dots & A_{N-2, 0} & A_{N-1, 0} \end{array} \right)\]

Hierbei lässt sich $A$ schrittweise approximieren durch die Berechnung von $A_0$, $A_1 \dots$, wobei $A_0$ am Rand die Werte von $g(x,y)$ übernimmt und ansonsten mit Nullen gefüllt wird.

Es gibt mehrere iterative numerische Verfahren, wovon das einfachste das Jacobi-Verfahren ist mit dem sogenannten 5-Punkt-Differenzenstern:

\[ A_{{k+1}_{i,j}} = \frac{1}{4} \left( A_{k_{i-1,j}} + A_{k_{i,j-1}} + A_{k_{i,j+1}} + A_{k_{i+1,j}} \right)\]

für $i, j \in 1 \dots N-1, k = 1, 2, \dots$. (Zur Herleitung siehe Alefeld et al, Parallele numerische Verfahren, S. 18 ff.)

Die Iteration wird solange wiederholt, bis

\[ \max_{i,j = 1 \dots N-1} \left| A_{{k+1}_{i,j}} - A_{{k}_{i,j}} \right| \le \epsilon\]

für eine vorgegebene Fehlergrenze $\epsilon$ gilt.

Aufgabe

Entwickeln Sie zunächst eine nicht parallelisierte Fassung, die mit Hilfe des Jacobi-Verfahrens eine numerische Lösung ermittelt. Sinnvoll ist eine Dimensionierung $100 \times 100$, dann werden nur knapp über 5.000 Jacobi-Schritte benötigt, um eine Genauigkeit von 1e-6 zu erreichen.

So können Sie Ihr Resultat visualisieren und in der Datei jacobi.jpg ablegen:
```
        #include <hpc/matvec/matrix2pixbuf.h>
        #include <hpc/aux/hsvcolor.h>
        
        /* ... */
        
        auto pixbuf = create_pixbuf(A, [](double val) -> HSVColor<double> {
           return HSVColor<double>((1-val) * 240, 1, 1);
        }, 8);
        gdk_pixbuf_save(pixbuf, "jacobi.jpg", "jpeg", nullptr,
           "quality", "100", nullptr);
        
```
Beim Übersetzen ist dann noch zusätzlich $(pkg-config --cflags gdk-pixbuf-2.0) anzugeben und beim Zusammenbauen $(pkg-config --libs gdk-pixbuf-2.0) am Ende der Kommandozeile.
Parallelisieren Sie das Jacobi-Verfahren, indem Sie die Matrix in Gruppen von Zeilen auf die zur Verfügung stehenden Prozesse aufteilen. Dann müssen die jeweils benachbarten Prozesse die Randzeilen untereinander austauschen.

Angenommen die Matrix $A$ wäre eine $11 \times 11$-Matrix und wir hätten drei Prozesse. Dann hätte jeder der drei Prozesse in jedem Schritt drei Zeilen neu zu berechnen (der Rand bleibt unverändert). Dann wären nach jedem Schritt folgende Übertragungen zwischen den Prozesse $P_1$, $P_2$ und $P_3$ notwendig:
- $P_1 \longrightarrow P_2: A_{3,1} \dots A_{3,9}$
- $P_2 \longrightarrow P_3: A_{6,1} \dots A_{6,9}$
- $P_3 \longrightarrow P_2: A_{7,1} \dots A_{7,9}$
- $P_2 \longrightarrow P_1: A_{4,1} \dots A_{4,9}$
Jede innere Partition erhält und sendet zwei innere Zeilen von $A$. Die Randpartitionen empfangen und senden jeweils nur eine Zeile.

Sie kommen hier in jedem Prozess mit zwei Aufrufen von MPISendrecv aus, einer Operation, die MPISend und MPI_Recv kombiniert und parallelisiert:
```
        int MPI_Sendrecv(const void* sendbuf, int sendcount, MPI_Datatype sendtype,
                         int dest, int sendtag,
           void* recvbuf, int recvcount, MPI_Datatype recvtype,
           int source, int recvtag,
           MPI_Comm comm, MPI_Status* status);
        
```
Die Randprozesse können bei dest bzw. source jeweils MPI_PROC_NULL, den sogenannten Nullprozess, verwenden, um die Kommunikation in die Randrichtung zu vermeiden. Dann könnten Sie im ersten Durchgang Zeilen aufwärts und im zweiten Durchgang abwärts übertragen.

Am Anfang empfiehlt es sich zunächst die Zahl der Schritte fest zu konfigurieren, damit Sie sich das Überprüfen des Abbruchkriteriums ersparen.

Um das globale Maximum zu bestimmen, empfiehlt sich die Kombination aus MPI_Reduce und MPI_Bcast. Mit MPI_Reduce erfährt der Prozess mit rank == 0 das globale Maximum, mit MPI_Bcast wird dieses dann an alle Prozesse verteilt.

        int MPI_Reduce(const void* sendbuf, void* recvbuf, int count,
                       MPI_Datatype datatype, MPI_Op op, int root,
         MPI_Comm comm);
        int MPI_Bcast(void* buffer, int count, MPI_Datatype datatype,
                      int root, MPI_Comm comm);
        

Für op kann hier MPI_MAX verwendet werden.

So lässt sich das Beispiel übersetzen und ausführen:

$shell> mpic++ -g -O3 -std=c++11 \
>    -I. -I/home/numerik/pub/hpc/session21 \
>    $(pkg-config --cflags gdk-pixbuf-2.0) \
>    -o jacobi jacobi.cpp $(pkg-config --libs gdk-pixbuf-2.0)
$shell> mpirun -np 4 jacobi
5090 iterations
$shell>

Am Ende können Sie auch gerne Ihre Lösung wieder zu einem tar-Archiv zusammenpacken und mit submit einreichen:

submit hpc session21 session21.tar