![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Oberon |
 | Hallo |
| Variablen |
 | Summe zweier Zahlen |
| Kontrollstrukturen |
 | Hilo-Game |
| Endliche Automaten |
 | Floating Point Automaton |
 | Minimum |
 | Tennis FSA |
| Formale Logik |
 | Logelei Familie Meier |
| Typen in Oberon |
 | Darstellungsprobleme bei Gleitkommazahlen |
 | Repr�sentierung von Gleitkommazahlen |
 | Zuf�lliges Mischen |
 | H�ufigkeitsstatistik f�r Buchstaben |
 | Transitive H�llen |
 | Adressbuch |
| Prozeduren |
 | Parameter�bergabe-Demonstrationen |
| Ein- und Ausgabe-Verbindungen |
 | In eine Datei schreiben |
 | Fortune Cookies |
| Argumente aus der Kommandozeile |
 | Kommandozeilen-Argumente |
 | Aneinanderh�ngen von Dateien |
 | Ausw�hlen von Feldern aus Texten |
| Sortierverfahren |
 | Sortieren von Datens�tzen |
| Testen |
 | Automatisierte Blackbox-Tests |
| Koroutinen |
 | Einfaches Beispiel mit Koroutinen |
 | Einfache Filter auf Basis interner Pipelines |
 | Virtuelle Tour mit Historie |
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Die Vorlesung Allgemeine Informatik I verfolgt zwei wesentliche Ziele:
 | Solide Einführung in das Fach der Informatik, so daß
später weiterführende Veranstaltungen besucht werden können.
Alle Kerngebiete der Informatik werden vertreten sein mit
Aspekten aus der theoretischen, praktischen und angewandten
Informatik.
|
 | Erlernung des fundierten praktischen Umgangs mit Rechnern.
Das geht bei uns deutlich darüber hinaus über das Finden
des richtigen Menüs und des richtigen Buttons. Es geht darum,
daß Sie das Innenleben Ihres Rechners oder Betriebssystems
verstehen lernen, so daß Sie in der Lage sind, selbst
für Ihre Arbeit notwendige Werkzeuge zu erstellen und somit
viel effizienter und effektiver mit Rechnern umgehen können.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Zu der Veranstaltung Allgemeine Informatik I zählen
 | die Vorlesung an jedem Dienstag, 15-17 Uhr im H22,
|
 | die Übungen an jedem Mittwoch, 14-16 Uhr im H4/5,
|
 | die Tutorien, die gruppenweise jede Woche an
mit Ihrem Tutor verabredeten Terminen stattfinden und
|
 | Ihre aktive Beteiligung durch das Nacharbeiten
der Vorlesung, Lösen von Übungsaufgaben, die Teilnahme an den
Tutorien und das Stellen von Fragen in allen Veranstaltungen,
per E-Mail oder in den Sprechstunden.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Da die Vorlesung weitgehend im Präsentationsstil gehalten wird,
droht gerade in der Informatik die Gefahr, daß die Notwendigkeit
einer aktiven Beteiligung unterschätzt wird.
|
 | Viele Vorlesungsinhalte wirken zunächst durchaus
``einleuchtend'' und es ist zu Beginn auch nicht schwierig,
ihnen zu folgen. Das gilt insbesondere dann, wenn zu Beginn
bereits Erfahrungen mit dem Umgang mit Computern vorliegen.
|
 | Es liegt jedoch in der Natur dieses Faches, daß viele subtile
aber wesentliche Feinheiten nur dann auffallen, wenn die
Übungsaufgaben zeitnah erledigt werden.
|
 | Später werden die aus den Übungen zu gewinnenden Kenntnisse
selbstverständlich vorausgesetzt.
|
 | Diejenigen, die die Übungsteilnahme zu Beginn unterschätzt
haben, weil die Vorlesung so leicht erscheint, erfahren dann irgendwann
im Laufe des Wintersemesters einen Moment, ab dem sie in der
Vorlesung völlig abgehängt werden. Das ist dann sehr frustrierend
für alle Beteiligten.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Tutorien werden in Gruppen zu 4 Studenten abgehalten.
|
 | Gruppen zu drei Studenten sind in Ausnahmefällen auch möglich.
|
 | Den Tutor können Sie während der ersten Übungsstunde
morgen wählen. Damit Sie eine Entscheidungsgrundlage haben,
werden die bevorzugten Termine für Tutorien der einzelnen
Tutoren bekannt gegeben.
|
 | Nutzen Sie bereits heute und morgen früh die Gelegenheit
zur Gruppenbildung.
|
 | Mit Ihrem Tutor treffen Sie sich einmal in der Woche
irgendwann zwischen Montag und Mittwoch-Vormittag.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Die Teilnahme an den Übungen setzt den Zugang zu unserer Rechner-Infrastruktur voraus. Zu folgenden Terminen können Sie eine Benutzungsberechtigung bei uns beantragen:
| Studiengang | Wochentag | Zeitraum |
| Mathematik und Wima | Mittwoch | 10-12 Uhr |
| E-Technik | Mittwoch | 16-18 Uhr |
| Physik und Wirtschaftsphysik | Donnerstag | 14-16 Uhr |
| alle anderen | Dienstag (heute!) | 17-18 Uhr |
Alle Termine finden in O27/213 statt. Sobald alle Anträge bearbeitet sind, gehen wir. Wir warten also nicht zwangsläufig bis zum Ende der genannten Zeiträume.
Bitte bringen Sie Ihren Studentenausweis (sofern Sie immatrikuliert sind) oder Ihren Personalausweis (bei Gasthörern) mit. Ohne Ausweispapiere können wir den Antrag nicht entgegen nehmen.
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sie reihen sich zu Ihrem Termin in eine Schlange und
warten, bis einer der Tutoren frei wird.
|
 | Der Tutor nimmt Ihre persönlichen Daten entgegen
(Name, Matrikelnummer, Studiengang) und gibt Ihnen
Gelegenheit, ein erstes Passwort einzutragen.
|
 | Achten Sie bitte darauf, daß Ihr Name korrekt
eingetragen wird. Sie werden genau die gleiche Schreibweise
später auf Ihrem Schein vorfinden.
|
 | Der Tutor läßt die Benutzungsrichtlinien ausdrucken,
die Sie unterschreiben müssen. Der Tutor zeichnet
die Richtlinien gegen.
|
 | Die unterschriebenen Benutzungsrichtlinien werden
gesammelt und bei unserem Sekretariat abgegeben, das
alle ordnungsgemäßen Anträge freischaltet.
|
 | Wenn alles klappt, haben Sie Ihren Zugang binnen
ein oder zwei Tagen. Das heißt, daß es spätestens
Ende dieser Woche klappen sollte.
|
 | Kontaktieren Sie uns bitte, falls es dabei Probleme
geben sollte.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Mit einer Benutzungsberechtigung bei uns übernehmen
Sie persönlich die Verantwortung für Ihren Zugang.
|
 | Diese beginnt mit der Wahl eines sicheren Passworts.
|
 | Das ist keine triviale Hürde, da gute Passwörter
nicht leicht zu erfinden sind und sich nur schwer
einprägen lassen.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgende Regeln sind zu beachten:
 | Das Passwort sollte genau 8 Zeichen lang sein.
(Kürzer ist zu kurz und alles hinter dem achten Zeichen
wird unglücklicherweise ignoriert).
|
 | Zugelassen sind alle Zeichen, die die Tastatur hergibt:
Klein- und Großbuchstaben, Ziffern, Sonderzeichen.
|
 | Vermeiden Sie Umlaute, ``ß'' und Funktionstasten.
|
 | Das Passwort darf keinem bekanntem Wort ähneln,
egal aus welcher Sprache. Genauso sind Namen, Ortsbezeichnungen,
Geburtsdaten, Auto-Kennzeichen, Telefonnummern usw. allesamt tabu.
|
 | Bei uns muß das Passwort mindestens einen Kleinbuchstaben und
einen Großbuchstaben haben und eines der ersten sieben Zeichen muß
ein Sonderzeichen sein.
|
 | Hinweis: Achten Sie darauf, daß nicht versehentlich
Caps-Lock oder Num-Lock aktiv sind!
|
 | Wenn wir feststellen, daß wir Ihr Passwort ``knacken''
können, wird Ihr Zugang gesperrt, bis Sie bei uns persönlich
vorbeischauen.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
101076 Somak4 challeng holsten1 mephisto sonne1 123asd Susanne! check-ma hxnmstr michael2 sonnensc 161065 TAbay1 claudia inges. micra1 sphinx 161072 Ukraine1 clemente island! mircea5 ssroessn 161278 Zhang!!! cleo19 jager. mkell1 stierle2 1anne1 abrahas cocis20 jkjkjk mopper striker 1lichtwa af5011 corvus joasia morisset struppi! 1quinn alegria cumulus1 joker1 mousse24 sunpol 1qwert alex95 departur jsschrst niomniom tania2 2beijing alexandr dg1nfv0 julius. orkork taraxacu 2callent algarve diekts junkie ortho9 thpolt1 2emacs angel! dingmin karmann oyster7 tiger1 2mannan antonia! eduardo! kashmir patrick1 trabitra 8baume anul99 elzbieta kermit peacock tsvg11 Allgaeu0 apmats eminem! kickers2 pepper1 tuartor Antimon! apollo13 erleucht konichiw peugeot3 tueanh Baller1 asterix0 euro97 kontroll popen7 tw0477 Berlin? avatar1 f7260h laminar5 popo96 verdik. Brckstdt babis1 fabio? leblanc prodigy vergil3 Cardix! barbara! fafnir! lespaul quasar vietnam EgkBaH basti1 falcon3 lichen/ quattro viktoria Gwaihir beast! front242 lothar1 quoniam voodoo2 Honey7 biblia1 furioso loulou1 rack21 wave43 Kinderzi bini11 ganter lucent radiatio werner LIEBE6 birten garfield madlen radies1 winter96 Mailand! blumensc ge1706 maicel revilo xxxxxx Moritz1 bmb850 gery4 mailman1 rotar! zaborav1 Ninja1 bochum! hammet2 mamusia roxana zeppez Ninurta bonzo9 harpe. marsh5 sanjuan1 zeppi. Pasquale boreal! hedwig! maruca scarface zhangyin Peppermi bullfrog heidi1 mathe1 sherry Philo! butterfl hijack matthi78 simone2 Reginald butthead himmelbl me3203 sobaka Sharon! carmen hofbraeu melanie8 sodom666 |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Gute Beispiele: iFm=AmSt rLK/1oeT
|
 | Spruch-Methode: Man wähle irgendeinen Satz,
beispielsweise ``Ich freue mich auf mein Studium'',
nimmt die Anfangsbuchstaben, variiert Groß- und
Kleinschreibung und wirft ein Sonderzeichen ein.
|
 | Zweiwort-Methode: Man wähle zwei Begriffe,
beispielsweise ``Erlkönig und Goethe'', nimmt
daraus nur Fragmente und läßt die beiden verbleibenden
Teile durch Sonderzeichen verbinden. Hier sollte
ebenfalls Groß und Kleinschreibung variiert werden.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Es ist nicht nur wichtig, daß Sie sich ein gutes Passwort ausdenken, sondern daß Sie damit auch richtig umgehen:
 | Nie aufschreiben!
Es ist nicht schlimm, wenn Sie Ihr Passwort vergessen.
Wenn Sie Ihren Studentenausweis dabei haben, können Sie
einen von uns aufsuchen und sich selbst ein neues Passwort
eintragen. Es empfiehlt sich, ein neues Passwort einzuüben,
indem Sie sich ein Dutzend mal hintereinander anmelden.
|
 | Lassen Sie sich nicht über die Schulter gucken bei
der Eingabe des Passworts. Wenn Sie den Verdacht haben,
daß jemand Ihr Passwort erspähen konnte, sollten Sie
sich sofort ein neues geben. Dies geht mit dem
passwd-Kommando.
|
 | Senden Sie Ihr Passwort nie im Klartext über das
Netzwerk. SSH (secure shell) ist gut, da hier
alles verschlüsselt wird. Bei POP und FTP werden
andere Passwörter verwendet.
|
 | Benutzen Sie nie potentiell mit Viren oder Würmern
verseuchte Rechner zur Anmeldung bei uns, da dann mit
Schnüffelprogrammen gerechnet werden muß, die die
Eingabe von Passwörtern abfangen.
|
 | Ein periodischer Passwort-Wechsel pro Jahr genügt.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Sie können bei uns frei einen Benutzernamen unter Beachtung folgender Regeln wählen:
 | Länge zwischen 2 und 8 Zeichen.
|
 | Besteht aus Kleinbuchstaben und Ziffern und muß mit
einem Kleinbuchstaben beginnen.
|
 | Er darf noch nicht vergeben sein.
|
 | Er wird nie wieder geändert!
|
Beachten Sie bitte die letzte Regel: Wir ändern unter keinen Umständen den Benutzernamen. Überlegen Sie sich also gut, ob Sie auch noch ``mausi'' heißen möchten, wenn Sie am Ende des Studiums Bewerbungen per E-Mail verschicken.
Im Falle von Namensänderungen (Urkunde/Ausweis bitte mitbringen) wird nur der ebenfalls eingetragene volle Name geändert, jedoch nie der Benutzername. Wir fügen aber in diesen Fällen gerne weitere Mail-Aliase hinzu, die den neuen Namen reflektieren.
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Sie haben viele Möglichkeiten, an unsere Rechner zu kommen:
 | Öffentliche Pool-Räume mit Chipkarten-Zugang:
| ||||||||
 | Öffentliche Pool-Räume in der Helmholtzstraße 18:
| ||||||||
 | Über SSH (secure shell) von einem beliebigen
(hoffentlich sicheren) Rechner auf einen unserer Server:
Alle diese Namen gehören zur Domain mathematik.uni-ulm.de.
Unter http://ssh.mathematik.uni-ulm.de/ gibt es Hinweise
zur Verwendung der SSH.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
In unseren Richtlinien geht es um folgende Punkte:
 | Es muß immer sichergestellt sein, wer für welchen
Zugang die Verantwortung trägt. Deswegen dürfen Sie nie
Ihren Zugang mit jemand anders teilen oder auch nur temporär
zur Verfügung stellen.
|
 | Sie dürfen die Sicherheit unserer Rechner nicht
gefährden. Das wäre beispielsweise der Fall, wenn es
jemand anders gelänge, an Ihren Zugang zu kommen.
|
 | Sie dürfen andere in der Benutzung unserer
Rechner-Ressourcen nicht behindern. Rechen- und speicherintensive
Anwendungen unterliegen daher strengen Richtlinien. Auch
der zur Verfügung stehende Plattenplatz ist aus diesem
Grunde reglementiert.
|
 | Der Zugang bei uns darf nur für Studienzwecke genutzt
werden.
|
Signifikante Verletzungen der Richtlinien führen zur temporären Sperrung eines Zugangs, bis der Vorfall durch einen persönlichen Besuch bei uns geklärt ist.
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sie dürfen ohne weitere Rückfragen 50 Megabyte auf Dauer
belegen.
|
 | Kurzfristig darf es auch deutlich mehr sein. Es gibt keine
Quota bei uns.
|
 | Wenn Sie über 50 Megabyte an einem Wochenende belegen, gibt
es eine warnende automatisch generierte E-Mail.
|
 | Wenn Sie diese E-Mails mehrfach ignorieren, führt dies
zur temporären Sperrung.
|
 | Wenn Sie für Studienzwecke wirklich mehr Plattenplatz
benötigen, erhöhen wir gerne Ihre Schranke. Eine E-Mail
an uns genügt.
|
 | Wie sich der benötigte Plattenplatz verringern läßt
und das Aufräumen funktioniert, wird in der nächsten Woche
vorgestellt.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Es stehen mehrere Laser-Drucker zur allgemeinen Verwendung
zur Verfügung:
| ||||||
 | Sie erhalten in jedem Semester ein Kontingent von 200 Seiten,
das in zwei Teilen zu jeweils 100 Seiten vergeben wird. Das heißt,
daß die zweite Hälfte erst irgendwann in der Mitte des Semesters
freigegeben wird.
| ||||||
 | Dieses Kontingent ist strikt nur für Studienzwecke zu
verwenden. Vorlesungsskripte dürfen nicht über unsere
Drucker ausgedruckt werden. Zulässig ist beispielsweise
der Ausdruck von Übungsblättern oder Ihrer Lösung zu
einem Übungsblatt.
| ||||||
 | Es wird dringend empfohlen, von den Druck-Möglichkeiten
beim KIZ Gebrauch zu machen (über Ihren KIZ-Zugang). Für
diese Drucker können Sie auch über den Unishop beliebig
weitere Kontingente nachkaufen. Entsprechend sind die Drucker
beim KIZ auch für den Ausdruck von Vorlesungsskripten geeignet.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Wir und die Tutoren verwenden ausschließlich Ihre
E-Mail-Adressen bei uns. Wenn Sie E-Mails weitergeleitet
haben möchten, finden Sie Hinweise dazu unter: http://www.mathematik.uni-ulm.de/admin/qmail/ |
 | Wir empfehlen Ihnen jedoch, E-Mails für Studienzwecke
direkt bei uns zu lesen und zu versenden. Das ist
viel zuverlässiger als die zahllosen Free-Mailer
und ist auch von außen über eine SSH erreichbar.
|
 | POP wird ebenfalls unterstützt, muß jedoch
von Ihnen selbst konfiguriert werden: http://www.mathematik.uni-ulm.de/admin/qmail/pop.html |
 | Wenn Sie auf einer Web-Schnittstelle bestehen,
empfiehlt sich der entsprechende Dienst beim KIZ.
|
 | Bitte versenden Sie keine E-Mails mit umfangreichen
Anhängen. Das übliche Limit liegt bei einem Megabyte.
|
 | Wenn Sie größere Datenmengen mit jemanden austauschen
möchten, geht dies auch mit individuellen FTP-Zugängen.
Mehr dazu unter: http://www.mathematik.uni-ulm.de/admin/adis-ftp/ |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Unsere Rechner und die Werkzeuge, die wir darauf einsetzen, wirken für viele Neulinge exotisch:
 | Bei unseren Rechnern handelt es sich um Arbeitsplätze
und Servern von Sun Microsystems. Diese Rechner haben
SPARC-Prozessoren, die zu der Familie der Intel-Prozessoren
in keiner Weise kompatibel sind.
|
 | Entsprechend ist es beispielsweise unmöglich, Produkte
von Microsoft darauf laufen zu lassen.
|
 | Als Betriebssystem wird Solaris eingesetzt. Dabei handelt
es sich um eine Variante des originalen UNIX. Linux und
das GNU-Projekt haben sich UNIX zum Vorbild genommen. Bei
uns haben Sie Gelegenheit, das Original kennenzulernen.
|
 | Noch exotischer ist der Wahl der Programmiersprache,
die für die Einführung in die Software-Entwicklung verwendet
wird. Oberon dürfte eher als Figur aus dem Sommernachtstraum
oder als Mond des Uranus bekannt sein, denn als Programmiersprache.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Bedenken Sie, daß wir keinen Volkshochschulkurs anbieten. Ziel ist es bei uns, daß Sie solide Grundlagen in der Informatik erhalten, die über die nur kurzfristig Nutzen bringende Vertrautheit mit zur Zeit populären Anwendungen und Programmiersprachen hinausgeht.
Wichtig für die Auswahl unserer praktischen Umgebung waren für uns folgende Kriterien:
 | Sie ist einfach. Wir wollen keine kostbare Vorlesungszeit
mit der Einführung irrelevanter Details und Komplexitäten
verlieren, die in kürzester Zeit wieder veraltet sind.
|
 | Sie folgt weitgehend internationalen Standards. Für die
Arbeitsumgebung unter UNIX oder Linux gibt es einen gemeinsam
befolgten IEEE-Standard.
|
 | Wenn es Sie interessiert, können Sie hinter die Kulissen
schauen und bis zum letzten Bit herausbekommen, wie es dahinter
funktioniert.
|
 | Bei Linux (das in der Benutzung Solaris
weitgehend ähnelt) haben Sie die Möglichkeit, zu sehen, wie
ein Betriebssystemskern funktioniert und bei den GNU-Werkzeugen
sind ebenfalls die Quellen allesamt öffentlich.
|
 | Bei Oberon sind unsere Quellen öffentlich und
Sie können auch hier das gesamte System mitsamt den Quellen
für den Compiler und die Bibliothek nach Hause nehmen.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgende Themen gehören zu Allgemeine Informatik I:
 | Kurze Einführung in unsere Arbeitsumgebung einschließlich
einer Einführung in das UNIX-Dateisystem und wichtige
Werkzeuge unter UNIX.
|
 | Einführung in die praktische Programmierung mit Oberon
einschließlich Datentypen (Basistypen, Arrays und Records),
Schleifen, Prozeduren, Rekursion, Ein- und Ausgabe und die
Einbettung in die UNIX-Umgebung.
|
 | Einführung in Sortier-Algorithmen.
|
 | Einführung in formale Sprachen und endliche Automaten.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Im Anschluß werden im Sommersemester folgende Themen angeboten:
 | Fortgeschrittene Rekursionstechniken einschließlich
Recursive-Descent-Parsing, Backtracking und
Branch-And-Bound-Verfahren.
|
 | Mehr zu formalen Sprachen.
|
 | Einführung in dynamische Datenstrukturen einschließlich
linearen Listen, Bäumen und Hash-Verfahren.
|
 | Einführung in die Modularisierung und objekt-orientierte
Programmierung.
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Bitte scheuen Sie sich nicht,
 | mitten in der Vorlesung oder in den Übungen Fragen zu stellen,
|
 | Ihren Tutor, den Übungsleiter Herrn Heidenbluth oder mich
mit fragenden oder kommentierenden E-Mails zu überschütten und
|
 | unsere Sprechstunden zu nutzen.
|
Eine erfolgreiche Vorlesungsveranstaltung ist nur möglich, wenn die Kommunikation beidseitig funktioniert.
So erreichen Sie mich:
E-Mail: borchert@mathematik.uni-ulm.de
Büro: Helmholtzstraße 18, Zimmer E02
Telefon: 0731/50-23572 und 0731/50-32110
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Entwicklung von UNIX begann 1969 als Thompson
eine wenig benutzte PDP-7 für die Entwicklung seines
``Space Travel''-Projekts requirierte.
Mehr dazu: http://www.bell-labs.com/history/unix/pdp7.html |
 | Für das Spiel wurde ein minimales Betriebssystem
einschließlich einem Dateisystem benötigt. Damit
wurde die Grundlage für UNIX gelegt.
|
 | Seit den 80er Jahren gibt es den sogenannten
POSIX-Standard für die UNIX-Umgebung, um möglichst
viele Gemeinsamkeiten unter den vielen existierenden
UNIX-Varianten zu pflegen. Die aktuelle Fassung davon
ist der IEEE Standard 1003.1 in der Fassung von 2004
zu finden unter http://www.opengroup.org/onlinepubs/009695399/toc.htm |
 | Es gibt viele populäre Implementierungen davon,
zu denen beispielsweise Solaris gehört (leitet sich
vom originalen UNIX ab), GNU/Linux, FreeBSD und die
anderen BSD-Varianten.
|
 | Selbst für Microsoft Windows gibt es durch das
Cygwin-Projekt eine POSIX-Umgebung --
allerdings mit Einschränkungen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Der Erfolg von UNIX begründet sich auf die
Verwendung von wenigen und sehr einfachen Abstraktionen.
| ||||||||||
 | In der Informatik ist eine Abstraktion eine möglichst
einfache und flexible Schnittstelle, hinter der sich viele
verschiedene komplexe Implementierungen verbergen können.
| ||||||||||
 | In folgenden Punkten bietet UNIX konkurrenzlos einfache
Abstraktionen an:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die wichtigste Schnittstelle unter UNIX für den
Benutzer ist die Kommandozeile.
|
 | Programme, die eine interaktive Kommandozeile anbieten,
werden unter UNIX Shells genannt. Davon gibt es nicht
wenige.
|
 | Bekannt sind insbesondere die Bourne Shell sh (praktisch
unverändert seit ca. 1980), die Korn Shell ksh (entstand
Ende der 80er Jahre) und die Bourne Again Shell bash aus
dem GNU-Projekt. Zeitweilig populär war auch noch die
C-Shell csh, die sich aber in der verwendeten Syntax
deutlich von den anderen Shells unterscheidet.
|
 | Per Voreinstellung starten bei uns neue Zugänge mit
der bash.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Eine interaktive Shell ist unermüdlich darin,
 | eine Eingabe-Aufforderung auszugeben (genannt Prompt,
besteht bei uns per Voreinstellung aus dem Namen des
Rechners, auf dem Sie gerade arbeiten, einem Dollar-Zeichen
und einem Leerzeichen),
|
 | eine Zeile einzulesen,
|
 | dies als Aufruf eines Programms mit einigen Parametern
zu interpretieren,
|
 | das ausgewählte Programm mit den Parametern zur
Ausführung zu bringen und
|
 | darauf zu warten, daß das Program beendet ist.
|
Eine interaktive Shell endet nur dann, wenn die Eingabe endet oder sie explizit terminiert wird.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Wenn Sie unter UNIX interaktiv etwas eingeben, haben normalerweise einige Zeichen eine besondere Bedeutung:
 | BACKSPACE löscht das zuletzt eingegebene
Zeichen in der aktuellen Eingabezeile.
|
 | CTRL-u (zuerst die ``Control''-Taste
drücken und während sie noch gedrückt bleibt, die Taste
``u'' drücken) löscht die gesamte Eingabezeile.
|
 | CTRL-w löscht das zuletzt eingegebene Wort.
|
 | RETURN beendet die aktuelle Eingabe mit
einem Zeilentrenner.
|
 | CTRL-d beendet die aktuelle Eingabe ohne
einen Zeilentrenner. Geschieht dies zu Beginn einer
Zeile (also ohne bislang eingetippten Zeileninhalt)
wird dies als Eingabe-Ende interpretiert.
|
 | CTRL-c sendet ein Signal an das gerade
laufende Programm, das normalerweise zur vorzeitigen
Terminierung führt.
|
 | CTRL-s stoppt die Ausgabe, die sich danach
nur mit CTRL-q wieder fortsetzen läßt.
|
 | CTRL-v nimmt dem folgenden Zeichen die
Sonderbedeutung.
|
All diese Funktionen können auf andere Zeichen belegt werden. Hier sind nur unsere Voreinstellungen genannt.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Eine Kommandozeile in einer Shell besteht im einfachsten
Falle aus
| ||||
 | Der Programmname und die Argumente werden durch
Leerzeichen (und Tabs) voneinander getrennt.
| ||||
 | Beispiel:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Mehrheit der zur Verfügung stehenden Programme
geben kurze hilfreiche Hinweise, wenn sie falsch
aufgerufen worden sind.
| |
 | Beispiel:
Hier beschwert sich cal darüber, daß es keinen
Monat mit der Nummer 2004 gibt.
| |
 | Die sogenannten Usage-Zeilen geben an, ob und wenn ja,
was für Argumente (Parameter) erwartet werden.
Die eckigen Klammern umfassen dabei optionale Argumente.
| |
 | Im konkreten Falle kann cal ganz ohne Argumente
aufgerufen werden (liefert den Kalender für den aktuellen
Monat) oder mit nur einem Argument (wird als Jahr
interpretiert und liefert den Kalender für ein ganzes Jahr)
oder mit zwei Parametern (Monat und Jahr; liefert dann den
Kalender für den Monat im genannten Jahr).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Für (fast) alle Kommandos gibt es sogenannte Manual-Seiten,
die kurz und präzise jeweils ein Kommando mitsamt all seinen
Aufrufmöglichkeiten erklären.
| |
 | Diese lassen sich am einfachsten mit dem man-Kommando
abrufen. Als Argument wird dabei der Name des Kommandos
übergeben, zu dem die Dokumentation gewünscht wird.
| |
 | Beispiel: man cal (gekürzte Ausgabe unter Solaris)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | NAME zeigt den Namen des Kommandos zusammen
mit einem Einzeiler, der das Kommando beschreibt.
|
 | SYNOPSIS gibt die Aufruf-Syntax des Programms an
analog zur Usage-Meldung.
|
 | DESCRIPTION beschreibt detailliert das Kommando
und spezifiziert genau wie die Argumente interpretiert
werden.
|
 | SEE ALSO verweist auf andere Manual-Seiten, die
in diesem Kontext interessant sind.
|
 | BUGS beschreibt Einschränkungen und verbliebene
bekannte Probleme des Kommandos.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Wenn Sie bei uns mit dem man-Kommando eine
Manualseite betrachten, landen Sie automatisch in
einem Programm, mit dem Sie den Text seitenweise
betrachten können.
| ||||||||||
 | Als Seitenbetrachter kommt bei uns per Voreinstellung
das Programm less zum Zuge.
| ||||||||||
 | Wichtige interaktive Kommandos innerhalb von less:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Der hierarchische Namensraum unter UNIX ist rekursiv definiert:
 | ``/'' ist ein Verzeichnis.
|
 | Jedes Verzeichnis beliebig viele Namen, die
keine ``/'' enthalten dürfen. Jedem Namen sind (normalerweise)
entweder Dateien oder weitere Verzeichnisse zugeordnet.
|
 | Innerhalb eines Verzeichnisses kommt kein Name mehrfach vor.
|
 | Ein Pfad besteht aus einer Liste von Namen, die durch
``/'' getrennt werden.
|
 | Beispiel: Wenn Ihr Benutzername ``hmueller'' lautet und
Sie jetzt in diesem Jahr bei uns begonnen haben, findet sich
Ihr sogenanntes Heimatverzeichnis unter
/home/theseus/2004/hmueller
Im sogenannten Wurzel-Verzeichnis ``/'' gibt es entsprechend
ein Verzeichnis namens ``home''. In diesem wiederum ein
Verzeichnis namens ``theseus'', darunter ein Verzeichnis
namens ``2004'', worunter wiederum das Verzeichnis ``hmueller''
zu finden ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Der Namensraum kann unter UNIX (in erster Näherung) als Baum gezeichnet werden, wobei die Verzeichnisse die Funktion von Ästen übernehmen und die Dateien den Blättern entsprechen. Nach Informatiker-Tradition wachsen Bäume von oben nach unten:

![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Jedem Prozeß (laufendes Programm) unter UNIX läßt sich
ein aktuelles Arbeitsverzeichnis zuordnen.
|
 | Wenn Sie sich bei uns anmelden, beginnt Ihre Shell in
Ihrem Heimatverzeichnis.
|
 | Mit dem cd-Kommando (change directory)
können Sie das aktuelle Arbeitsverzeichnis für die
Shell wechseln.
|
 | Beispiel: cd uebungen
|
 | Wenn Sie bei cd kein Verzeichnis angeben, landen
Sie wieder in Ihrem Heimatkatalog.
|
 | Mit pwd (print working directory) erfahren
Sie, in welchem Verzeichnis Sie sich gerade befinden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Absolute Pfadnamen beginnen immer von der Wurzel,
also mit einem ``/''.
|
 | Relative Pfadnamen beginnen von dem aktuellen Verzeichnis.
|
 | Beispiel: Ausgehend von Ihrem Heimatkatalog können Sie
mit uebungen/Hallo.od die Datei Hallo.od unter dem
Verzeichnis uebungen benennen.
|
 | In jedem Verzeichnis gibt es die speziellen Namen
. und ... Mit .. läßt sich das übergeordnete
Verzeichnis erreichen, mit . wird das eigene Verzeichnis
erreicht.
|
 | Beispiel: Wenn Sie in dem Verzeichnis uebungen sind
können Sie mit cd ../bin in Ihr bin-Verzeichnis
wechseln.
|
 | Einige Shells, insbesondere die bash und die ksh
interpretieren ~ als Ihr Heimatverzeichnis.
|
 | Beispiel: Mit cd ~/uebungen können Sie immer mit einem
Kommando in Ihr uebungen-Verzeichnis wechseln unabhängig
von Ihrer aktuellen Position.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Mit dem ls-Kommando erhalten Sie eine Aufzählung
der Namen in Ihrem aktuellen Verzeichnis.
| |
 | Sie können auch einen Pfadnamen angeben, um sich den
Inhalt eines Verzeichnisses anzusehen, ohne dorthin
zu wechseln. Beispiel: ls ~/uebungen
| |
 | Per Voreinstellung werden bei uns Farben verwendet und
Verzeichnisse werden dann blau dargestellt.
| |
 | Wenn Farben nicht zur Verfügung stehen, können Sie
bei uns auch alternativ f verwenden (ein kurzes
Synonym für ls -FC), das hinter Verzeichnisnamen einen
Schrägstrich anfügt und hinter ausführbaren Programmen
einen Stern.
| |
 | Mit der Option -l erhalten Sie bei ls
nicht nur Namen, sondern weitere sehr ausführliche Angaben:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Unter UNIX sind Dateien endliche Sequenzen von
ganzen Zahlen aus dem Bereich 0 bis 255.
|
 | Für jede dieser Zahlen werden zur Repräsentierung
8 Bits benötigt, die zusammengefaßt als Byte
bezeichnet werden.
|
 | Das UNIX-System interpretiert normalerweise nicht
den Inhalt von Dateien. Die einzige Ausnahme sind
ausführbare Programme.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Bei Texten denken wir zunächst an Bücher oder andere
Publikationen mit vielen verschiedenen Schriftarten,
Farben und Grafiken.
|
 | Wenn Texte jedoch auf einem digitalen Datenträger
zu repräsentieren sind, müssen wir all dies in
einer geeigneten Form kodieren.
|
 | Die Kodierung beginnt damit, jedem Schriftzeichen
eine Nummer zuzuweisen. Hierfür gibt es den Unicode-Standard,
der beispielsweise den lateinischen Buchstaben ``A'' der Nummer
65 zuordnet.
|
 | Diese Kodierung bezieht sich nur auf Schriftzeichen und
nicht auf die Schriftgröße, den konkreten Zeichensatz
(wie Helvetica oder Times Roman) oder Schriftarten
(wie kursiv oder fett).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
\documentclass[12pt]{article}
\usepackage{german}
\begin{document}
Hallo, hier ist etwas Text,
der mit \LaTeX{} gesetzt wurde.
{\bf Hier ist etwas Fettdruck},
{\Large hier etwas gro"se Schrift}
und {\it hier etwas kursiver Text}.
\end{document}
|
 | Wenn bereits eine erste Kodierung für Schriftzeichen
vorliegt, können auf dieser Ebene leicht Sprachen definiert
werden, die Texte in all ihrer Vielfalt beschreiben können.
|
 | Ein Beispiel dafür ist das \TeX-System von Donald Knuth
bzw. das darauf basierende \LaTeX-Paket.
|
 | Hier liegt der Schwerpunkt darauf, daß die Kodierung
für den Menschen gut lesbar und bearbeitbar ist.
|
 | Mit entsprechenden Programmen kann diese Kodierung
in viele andere Kodierungen übertragen werden, die
von Druckern verstanden werden (z.B. PostScript) oder die
am Bildschirm betrachtbar sind (z.B. PDF). Auch diese
Kodierungen sind wiederum Text in vorgegebenen Sprachen, die
den gewünschten Ausgabetext in all seiner Vielfalt
beschreiben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Bislang erschien die Ausgabe der von uns aufgerufenen
Kommandos direkt auf dem Shell-Fenster und die Eingabe
wurde direkt von der Tastatur eingelesen.
| |
 | Die Ein- und Ausgabe lassen sich umlenken.
So kann beispielsweise die Ausgabe in eine Datei
erfolgen oder die Eingabe aus einer Datei eingelesen
werden.
| |
 | Beispiel:
Mit > wurde die Ausgabe in eine Datei umgelenkt.
Der Name der Ausgabedatei folgt dabei dem Winkel.
Mit dem cat-Kommando können eine oder mehrere
Dateien hintereinander gehängt ausgegeben werden
(der Name cat leitet sich von concatenate
ab).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die umlenkbaren Ein- und Ausgabe-Kanäle werden
als Standard-Eingabe und Standard-Ausgabe bezeichnet.
| |
 | Das Kommando bc ist als Taschenrechner
mit beliebig großen Zahlen (soweit der Speicher
reicht) nutzbar. Beispiel:
Hier wurde die auszurechnende Formel direkt vom
Benutzer eingelesen. Das Eingabeende erfolgte
mit CTRL-d.
| |
 | Mit dem cat-Kommando könnten wir jedoch
eine Datei mit der Formel füllen und diese
später dem bc-Kommando füttern:
Wenn cat keine Argumente erhält, wird von
der Standard-Eingabe gelesen. Dies wird wiederum
durch CTRL-d beendet, wenn Sie direkt vom Benutzer
erfolgt. Mit < wird die Standard-Eingabe umgelenkt
unter der Verwendung der Datei, deren Name folgt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Mit >> ist es auch möglich, die Standard-Ausgabe
an eine Datei hinten anzuhängen. Beispiel:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Standard-Ausgabe eines Kommandos kann direkt
zur Standard-Eingabe eines folgenden Kommandos werden.
| |
 | Beispiel:
| |
 | Hier gibt das Kommando ls alle Dateien aus
dem Verzeichnis /usr/bin aus. Diese Ausgabe ist
aber nicht zu sehen, sondern wird zur Standard-Eingabe
des folgenden Kommandos grep. Diese Verknüpfung
erfolgt durch den senkrechten Strich, der im UNIX-Jargon
als Pipeline bezeichnet wird.
| |
 | grep selektiert
die Zeilen aus der Standard-Eingabe, die ein gegebenes
Muster erfüllen. Hier werden nur die Zeilen ausgegeben,
in denen die Buchstabenfolge ``cal'' irgendwo auftaucht.
| |
 | Auch längere Pipeline-Ketten sind möglich:
wc -l gibt aus, wieviel Zeilen in der Standard-Eingabe
vorgefunden worden sind. wc steht dabei für
word count.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Mit mkdir kann ein Verzeichnis angelegt werden. Beispiel: mkdir uebungen |
 | Mit rm kann eine Datei gelöscht werden
(rm steht für remove). Vorsicht: Diese
Operation läßt sich nicht rückgängig machen. Beispiel: rm Hallo.od |
 | Mit rmdir lassen sich leere Verzeichnisse entfernen.
|
 | Mit cp lassen sich Dateien kopieren. Beispiel: cp Hallo.od NeuesHallo.od |
 | Mit mv lassen sich Dateien umtaufen oder verschieben. Beispiel für das Umtaufen: mv Hallo.od NeuesHallo.od (Vorsicht: Falls es NeuesHallo.od vorher gab, ist es nun verloren gegangen!). Beispiel für das Verschieben: mv ~/Hallo.od . (Verschiebt Hallo.od aus dem Heimatverzeichnis in das aktuelle Verzeichnis). |
 | Philosophie dieser Kommandos: Was der Benutzer möchte,
wird klaglos erledigt. Er ist intelligent und weiß, was er möchte.
Wenn alles glatt geht, erfolgt keine Ausgabe.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Viele Programme unterstützen folgende Konventionen:
 | Die ersten Argumente sind Optionen, d.h.
optionale Argumente. Diese werden üblicherweise
mit einem Bindestrich eingeleitet und von einem Buchstaben
gefolgt. Beispiel: ls -l oder wc -l
|
 | Wenn mehrere Optionen angegeben werden, können
diese zusammengefaßt oder auch getrennt voneinander
angegeben werden. Beispiel: ls -a -l (-a bittet ls darum, alle Namen aufzuzählen, auch solche die mit einem Punkt beginnen). Alternativ: ls -la |
 | Nach den Optionen folgen Dateinamen, aus
denen das Programm einliest. Wenn keine Dateinamen
angegeben wird, erfolgt die Eingabe aus
der Standard-Eingabe. Beispiel: cat
|
 | Wenn der erste Dateiname mit einem Bindestrich
beginnt, kann mit einem vorausgehenden doppelten
Bindestrich -- die Interpretation als Dateiname
erzwungen werden. Beispiel: rm -- -x (Löscht die Datei mit dem Namen ``-x''). |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Editor ist ein anderes Wort für Herausgeber.
| ||||||||
 | In der Informatik werden Programme zur Erstellung
und Bearbeitung von Texten ebenso als Editoren
bezeichnet.
| ||||||||
 | Zu den wichtigsten Funktionalitäten eines
Editors gehört es,
| ||||||||
 | Da die Struktur des Textes so einfach ist, lassen sich
auch sehr leicht aufwendigere Operationen realisieren. Dazu
gehört beispielsweise das Ausführen von Textänderungen für
alle Teilsequenzen, die bestimmten Textmustern entsprechen.
| ||||||||
 | In der Welt von UNIX bzw. GNU/Linux gibt es zwei Familien
von mächtigen Editoren, die große Popularität erlangten:
Emacs und vi.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Durch die Einführung graphischer Benutzungsoberflächen
wurden Textsysteme populär, bei denen auf dem Schirm der
Text bereits in seiner endgültigen Form dargestellt wird
(WYSIWYG = what you see is what you get).
|
 | Das hat zur Folge, daß die Kodierung vor dem Benutzer
versteckt wird. Bei einigen Systemen (wie z.B. Microsoft Word)
ist diese Kodierung proprietär und ändert sich bei jeder
neuen Version.
|
 | Nicht-offene Kodierungen werden rasch zum ``Datengrab'',
da nur die zugehörige Anwendung die Kodierung interpretieren
und in andere Formen überführen kann. Neue Versionen oder
auslaufende Lizenzen können zum Verlust des Textes führen.
|
 | Im übrigen läßt sich der WYSIWYG-Anspruch in der Praxis
nicht halten, da Ausdruck und Bildschirmanzeige voneinander
deutlich abweichen können.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Übersetzer gängiger Programmiersprachen erwarten
den Programmtext in Form einer Sequenz von Schriftzeichen.
Teilweise wird Unicode in voller Allgemeinheit akzeptiert,
teilweise nur Unterbereiche davon (z.B. ASCII oder ISO-Latin-1).
|
 | Entsprechend sind traditionelle Text-Editoren sehr
beliebt zur Erstellung von Programmtexten. Sie bieten auch
sehr umfangreiche Funktionalitäten, um Programmiertexte
gut lesbar zu formatieren und effizient zu bearbeiten.
|
 | Viele Programmiersprachen kommen mit Konventionen,
wie Programmtext in gut lesbarer Form auszusehen hat.
|
 | Üblich ist auch die farbliche Hervorhebung von
einzelnen Elementen des Programmtextes (in Abhängigkeit
von der verwendeten Programmiersprache). Diese Hervorhebungen
werden nicht im Programmtext selbst gespeichert, sondern
allgemein für bestimmte Programmiersprachen oder Editier-Modi
konfiguriert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | vi steht für ``visual editor''.
|
 | Die ursprüngliche Version wurde 1976 von Bill Joy
entwickelt als bildschirmorientierte Alternative zum
zeilenorientierten Editor ed. Aus einem Interview
des Linux-Magazins:
``What happened is that Ken Thompson came to Berkeley and brought this broken Pascal system, and we got this summer job to fix it. While we were fixing it, we got frustrated with the editor we were using which was named ed. ed is certainly frustrating. We got this code from a guy named George Coulouris at University College in London called em -- Editor for Mortals -- since only immortals could use ed to do anything. So we modified em and created en. I don't know if there was an eo or an ep but finally there was ex. I remember en but I don't know how it got to ex. So I had a terminal at home and a 300 baud modem so the cursor could move around and I just stayed up all night for a few months and wrote vi.'' |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Der vi wurde Ende der 70er Jahre und Anfang der 80er Jahre
kontinuierlich weiterentwickelt und gehört seitdem zu den
Standardwerkzeugen unter UNIX.
|
 | Leider war der Quelltext für den vi durch die
Kooperation mit AT&T proprietär, so daß für freie
Software-Systeme (wie GNU/Linux) der vi neu entwickelt
werden mußte. All diese Varianten bemühten sich (mehr
oder weniger erfolgreich), die originalen Kommandos des
vi zu implementieren und zusätzliche Funktionalitäten
anzubieten.
|
 | Besondere Popularität genießt hier heute der vim
(vi improved). Diesen Editor gibt es für alle
gängigen Plattformen unter http://www.vim.org/.
|
 | Auf unseren Systemen steht sowohl das Original (vi)
als auch der in der Funktionalität weit darüber hinausgehende
vim zur Verfügung.
|
 | Benutzern von Microsoft-Windows-Systemen sei es
aber empfohlen, vim im Rahmen von Cygwin zu installieren. Siehe http://www.cygwin.com/ |
 | Einen Überblick über alle bekannten Versionen des vi
liefert die Seite von Sven Guckes unter http://www.vi-editor.org/ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Der vi arbeitet grundsätzlich mit seiner eigenen Kopie
des zu bearbeitenden Textes.
| ||||
 | Es ist möglich, den vi ohne weitere Kommandozeilenargumente
aufzurufen. Dann beginnt der vi mit einem leeren Text.
| ||||
 | Wenn beim Aufruf des vi der Name einer Datei angegeben
wird, dann überprüft vi zuerst, ob es diese Datei bereits gibt:
| ||||
 | Eine Sicherung der vi-eigenen Kopie in eine Datei
erfolgt nur durch ausdrückliche Kommandos.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die unterste Zeile ist für Statusangaben reserviert
und die Eingabe längerer Kommandos.
|
 | Alle anderen Zeilen dienen zur Anzeige des zu
bearbeitenden Textes.
|
 | Um leere Zeilen vom Textende unterscheiden zu können,
werden nicht im Text vorhandene Zeilen mit einem führenden
`` '' markiert.
|
 | Zu Beginn wird oben der Anfang des eingelesenen Textes
angezeigt und der Cursor steht auf dem ersten Zeichen der
ersten Zeile.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Falls Sie sogleich in Panik den vi wieder verlassen möchten:
 | Durch die Eingabe eines ``Q'' können Sie den vi
sofort verlassen --- sofern Sie noch im anfänglichen
Modus sind und keine Veränderungen vorgenommen haben.
| ||||||
 | Alternativ können Sie mit ``ZZ'' die Veränderungen
abspeichern und den Editor verlassen.
| ||||||
 | Falls das nicht hilft, weil Sie sich unglücklicherweise
in einem anderen Modus befinden, die Datei verändert wurde,
aber noch kein Dateiname bekannt ist oder Sie auf sonstige
Weise im Krieg mit dem vi sind, hilft im Notfall folgende Sequenz:
Warnung: Diese Prozedur führt zur zwangsweisen Beendigung
Ihrer vi-Sitzung. Eine Sicherung Ihres möglicherweise
geänderten Textes findet dabei nicht statt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Monotone Rechenaufgaben haben schon seit vielen
Jahrhunderten Tüftler bewegt, Maschinen zu konstruieren,
die diese Aufgabe abnehmen können.
|
 | Im 16. Jahrhundert entwarf Leonardo da Vinci eine
Rechenmaschine. Entsprechende Notizen wurden 1967
entdeckt. Es gibt jedoch keine Hinweise, daß diese
zu Zeiten von Leonardo da Vinci gebaut worden wäre.
|
 | 1623 entwickelte und baute der Astronom und Mathematiker
Wilhelm Schickard die erste bekannte Rechenmaschine, die alle
vier Grundrechenarten beherrschte.
|
 | 1645 wurde von Blaise Pascal die zweite bekannte
Rechenmaschine gebaut.
|
 | 1668 wurde die erste nicht-dezimale Addiermaschine für
die englische Währung von Sir Samuel Morland gefertigt.
|
 | 1673 baute Gottfried Leibniz eine Rechenmaschine, die
neben den Grundrechenarten auch Wurzeln ziehen konnte.
|
 | 1786 entstand die ``Differenzmaschine'' von J. M. Mueller
entwickelt, die es erlaubte, Polynome zu tabulieren.
|
 | 1801 entstand die automatisierte Web-Maschine von
Joseph-Maire Jacuard, die mit Lochkarten programmiert
wurde.
|
 | 1820 entstand der erste in Massen produzierte Rechner
von Charles Xavier Thomas de Colmar, der über 90 Jahre
lang verkauft wurde.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Da nicht jeder eine Rechenmaschine zur Verfügung hatte,
gewannen viele Rechenhilfe große Popularität, zu denen
insbesondere Tafeln für Logarithmen und trigonometrische
Funktionen gehörten.
|
 | Eine der ersten Logarithmentafeln entstand 1620 von
Henry Briggs.
|
 | Mit zunehmenden Ansprüchen aus Astronomie, Vermessungswesen
und dem Ingenieurswesen wurden immer umfangreichere Tabellenwerke
benötigt, die in mühseliger Handarbeit von Scharen an
Mitarbeitern erstellt wurden. Das war zeitaufwendig, teuer
und auch sehr fehleranfällig.
|
 | Charles Babbage (1791-1871) versuchte, den ersten
generell programmierbaren Rechner zu bauen einschließlich
Lochkarten, frei nutzbarem Speicher und einem Drucker.
Seine ``Analytic Engine'' wurde jedoch zu seinen Lebzeiten
nie funktionsfähig. Seine hinterlassenen Teile und
Aufzeichnungen ermöglichten später einen Nachbau durch
das London Science Museum, der die Funktionsfähigkeit
seines Entwurfs belegte.
|
 | Ada Lovelace unterstützte Babbage und entwarf auf
Papier Programme für die ``Analytic Engine''. Sie ist
damit die erste Programmiererin in der Geschichte.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | 1938 baute Konrad Zuse einen mechanischen Rechner,
das Binärsystem verwendete (Z1).
|
 | 1939 entwickelten John V. Atanasoff und Clifford Berry
eine 16-Bit-Addiermaschine auf Basis von Röhren.
|
 | 1939 konstruierte Konrad Zuse eine Rechenmaschine
auf Basis von elektrischen Relays (Z2).
|
 | 1940 wurde bei den Bell Laboratories der
``Complex Number Calculator'' entwickelt, für den
Bauteile von Telefon-Verbindungsanlagen verwendet wurden
und der über Fernschreiber bedient werden konnte.
|
 | 1941 entstand der erste programmierbare Rechner,
der jedoch noch keine bedingten Sprünge unterstützte
von Konrad Zuse (Z3).
|
 | 1943 entstand ``Harvard Mark I'' als programmierbarer
Rechner von Howard H. Aiken und seinem Team.
|
 | 1943: ``I think there is a world market for maybe five
computers.'', Thomas Watson, Vorstandsvorsitzender von IBM.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | 1943 wurde ein spezialisierter Rechner zum Knacken
von Chiffren entwickelt von Max Newman, Wynn-Williams und
deren Team, zu dem auch Alan Turing gehörte.
Später wurde ``Collossus'' gebaut, der es erlaubte eine
programmierbare logische Funktion auf ein Eingabe-Band
mit einer Geschwindigkeit von 5000 Zeichen pro Sekunde
auszuführen.
|
 | 1946 entstand der erste vollständige elektronische
Computer (ENIAC = Electronic Numerical Integrator and Computer)
von John W. Mauchly und J. Presper Eckert am
Ballistic Research Laboratory.
|
 | 1948 entstand der erste Rechner, der sowohl das Programm
als auch die Daten im Speicher verwaltete
(SSEM = Small Scale Experimental Machine) am Manchester University.
|
 | 1951 wurde der erste universell programmierbare
Rechner (UNIVAC-1) von J. Presper Eckert and John Mauchly
entwickelt und gebaut.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Programmierbare Rechenmaschinen benötigen ein Funktionsmodell, das beschreibt, wie die Programm-Instruktionen ausgeführt werden. Es gibt zahlreiche verschiedene Funktionsmodelle:
Theoretische Modelle:
 | Lambda-Kalkül, wurde in den 30er Jahren von
Alonzo Church und Stephen Kleene entwickelt
zur theoretischen Untersuchung der Berechenbarkeit.
|
 | Turing-Maschine, wurde von Alan Turing entwickelt,
ebenfalls für theoretische Untersuchungen.
|
 | Zelluläre Automaten, die insbesondere durch
die Arbeiten von John Horton Conway bekannt wurden.
|
Praktische Rechner-Architekturen:
 | Die John-von-Neumann-Maschine die ist zugrundeliegende
Architektur fast aller Rechner von heute. Wesentliches Merkmale
sind die gemeinsame Nutzung des Speichers für Daten und
Programme und die Trennung zwischen Recheneinheit und Speicher.
|
 | Im Vergleich dazu sieht die Harvard-Architektur die
Trennung zwischen Daten und Programmen vor. Namensgeber
war die ``Harvard Mark I''.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Wurde von John von Neumann, John William Mauchly
und J. Presper Eckert beim ENIAC-Projekt entwickelt.
|
 | Der Speicher besteht aus n Speicherzellen, die
individuell addressiert werden können.
|
 | Über das Bus-System ist es möglich, einen
Lesebefehl und eine Adresse aus dem Bereich [0..n-1]
anzugeben. Kurz darauf kopiert das Speichersystem den Inhalt
der entsprechenden Zelle in den Bus. Umgekehrt kann auch
über den Bus ein
Schreibbefehl zusammen mit einer Adresse und dem Wert einer
Speicherzelle gegeben werden und der Speicher kopiert dann den
Wert in die entsprechende Zelle.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Recheneinheit hat weitere Speicherzellen,
die ihr direkt zugänglich sind. Diese werden
Register genannt. Dazu zählen insbesondere der
Befehlszähler, ein Register für den aktuellen Befehl
und weitere allgemein verwendbare Register.
| ||||||||||
 | Zu Beginn eines Rechenschritts wird die vom
Befehlszähler adressierte Speicherzelle in das
Befehls-Register geladen.
| ||||||||||
 | Danach wird der Befehlszähler um 1 erhöht.
| ||||||||||
 | Der Befehl wird dann dekodiert und ausgeführt.
| ||||||||||
 | Im Rahmen eines Befehls ist es u.a. möglich,
| ||||||||||
 | Wenn der Befehl fertig ausgeführt ist, wiederholt sich
diese Abfolge.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Bei Rechner-Architekturen gibt es zwei Sichten:
 | Sicht des Programmierers: Hier ist das Modell
(abstrakte Architektur)
relevant einschließlich der zur Verfügung stehenden
Register, des Adreßraumes, des Speichers und insbesondere
die zur Verfügung stehenden Instruktionen.
|
 | Sicht des Hardware-Ingenieurs: Hier geht es darum,
wie ein Modell konkret durch Hardware implementiert
werden kann. Viele Einzelkomponenten sind notwendig,
um ein funktionierendes System zu bauen: Prozessor,
Hauptplatine, Speicher-Chips, Ein- und Ausgabegeräte.
|
Zu einer abstrakten Architektur gibt es häufig zahlreiche Implementierungen. So läuft beispielsweise ein Programm, das für den Intel 80386-Prozessor in den 80er Jahren geschrieben worden ist, auch heute noch auf einem System mit einem Pentium-IV-Prozessor.
Es gibt zahlreiche verschiedene abstrakte Architekturen, die nicht miteinander kompatibel sind. Unsere Maschinen von Sun verwenden beispielsweise die SPARC-Architektur. Programme für die SPARC-Architektur laufen nicht auf den Intel-Prozessoren und umgekehrt.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Redcode ist ein kleines übersichtliches Beispiel für eine abstrakte Rechner-Architektur:
 | Redcode wurde zum ersten Mal vorgestellt in
der Kolumne ``Computer Recreations'' der Zeitschrift
Scientific American im Mai 1984 von A. K. Dewdney.
|
 | Das klassische Redcode-Modell kommt mit 8000
Speicherzellen und 8 verschiedenen Instruktionen aus.
|
 | Auf allgemeine Register wurde verzichtet. Stattdessen
werden arithmetische Operationen direkt auf den
Speicherzellen ausgeführt. Dies wäre weniger praktisch
für eine Architektur, die in Hardware gegossen wird,
aber Redcode wird nur emuliert, d.h.&,durch Programme
auf normalen Maschinen simuliert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Befehle haben in Redcode ein oder zwei Operanden, die jeweils entweder einen Wert direkt angeben oder eine Speicherzelle direkt oder indirekt adressieren:
| MOV | A, B | Kopiere den Wert von A nach B |
| ADD | A, B | Ersetze den Wert von B durch die Summe von A und B. |
| SUB | A, B | Ersetze den Wert von B durch die Differenz von A und B. |
| JMP | A | Springe nach A. |
| JMZ | A, B | Springe nach A, falls B den Wert 0 hat. |
| JMG | A, B | Springe nach A, falls B einen Wert ungleich 0 hat. |
| DJN | A, B | Dekrementiere B um 1 und springe nach A, falls B noch nicht 0 wurde. |
| CMP | A, B | Vergleiche A und B und überspringe die nächste Instruktion, falls die beiden Werte nicht übereinstimmen. |
Hinweis: Bei Sprüngen wird ein neuer Wert in den Befehlszähler geschrieben.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Jeder der beiden Operanden eines Befehls kann auf verschiedene Weise adressiert werden:
 | Konstante: Es wird keine Speicherzelle adressiert,
sondern der gewünschte Wert ist direkt in dem Befehl
enthalten.
|
 | Direkt: In dem Befehl steht eine Adresse, die
relativ zum (alten, noch nicht inkrementierten)
Wert des Befehlszählers interpretiert wird. Das
heißt, daß implizit der Befehlszähler zur Adresse
addiert wird. Ist das Resultat größer oder gleich
8000, wird durch 8000 geteilt und der Rest genommen
(aus 8000 wird so 0, aus 8001 entsprechend 1 usw.).
|
 | Indirekt: Zunächst wird wie bei der direkten
Adressierung der Inhalt einer Speicherzelle geladen.
Dann wird diese ebenfalls als Adresse interpretiert,
die relativ zur vorher adressierten Speicherzelle
interpretiert wird.
|
Solche Adressierungsmodi sind auch typisch für real existierende Prozessoren. Allerdings wird typischerweise mit Hilfe von Registern indirekt adressiert.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Redcode wurde für ein interessantes Computer-Spiel konzipiert:
 | Zwei beliebige Programme werden an zufällig bestimmten
Stellen in den Speicher geladen.
|
 | Die Recheneinheit gibt es doppelt, d.h. für jeden
der beiden Programme wird ein Befehlszähler verwaltet.
|
 | Die Speicherzellen sind entweder mit einem Datenwert
gefüllt oder einem Befehl. Alle nicht von den beiden
Programmen belegten Speicherzellen haben zu Beginn den
Datenwert 0.
|
 | Abwechselnd wird jeweils ein Befehl eines der beiden
Programme ausgeführt.
|
 | Sobald eines der beiden Programme versucht, einen
Datenwert als Befehl auszuführen, hat es verloren.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
;;; DWARF, as originally described by A.K. Dewdney. ptr DAT #0 start ADD #5,ptr MOV #0,@ptr JMP start |
 | Dieses Programm besteht aus einem Datenwert
und drei Befehlen.
|
 | Ein # vor einem Operanden gibt an, daß es
sich um eine Konstante handelt, @ kennzeichnet
eine indirekte Adressierung.
|
 | Der ADD-Befehl erhöht den Datenwert jeweils
um 5.
|
 | Der MOV-Befehl speichert den Datenwert 0 in
die Speicherzelle, auf die der Datenwert vor
dem ADD-Befehl verweist.
|
 | Der JMP-Befehl springt wieder zum ADD-Befehl.
|
 | Dieses Programm legt also im gesamten Speicher
in jeder 5. Speicherzelle eine 0 ab.
|
 | Wenn so eine Daten-0 in ein fremdes Programm fällt,
sind die Chancen gut, daß der Gegner verliert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
0 0 2 0 5 1 -1 1 0 0 2 -2 4 1 -2 |
 | In den Speicherzellen einer Maschine werden
Befehle mit Nummern kodiert. Im obigen Beispiel
repräsentiert 0 ein Datenfeld, 1 einen MOV-Befehl,
2 eine ADD-Befehl und 4 steht für JMP.
|
 | Operanden bestehen hier jeweils aus zwei
Zahlen: Die erste spezifiziert den Adressierungsmodus
und die zweite den Wert.
|
 | Da es sehr unbequem ist, Programme in dieser
Form einzugeben, wurden sogenannte Assembler
entwickelt, bei denen die Befehle Namen statt
Nummern haben und die Symbole für Programmpositionen
unterstützen. Auf diese Weise entfällt das Zählen
von Befehlen, um eine Distanz korrekt zu berechnen.
|
 | Wenn Programme unabhängig von einer konkreten
Architektur sein sollen, dann werden Programmiersprachen
(wie Oberon) interessant, die für verschiedene
Architekturen übersetzt werden können.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Programmiersprachen |
 | Maschinennahe Sprachen |
 | Höhere Programmiersprachen |
 | Einfachheit vs Kompliziertheit |
 | Vom Programmtext zur Ausführung |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Eine Programmiersprache wird durch zwei Komponenten definiert:
 | Die Syntax, die durch eine formelle Grammatik
beschrieben wird, spezifiziert welche Programmtexte zulässig
für die Programmiersprache sind und welche nicht.
|
 | Die Semantik beschreibt, welche Bedeutung Programmtexte
haben. Es gibt verschiedene formelle Methoden, die
Semantik einer Programmiersprache zu spezifizieren
(Beispiele: operationelle, denotationelle und
axiomatische Semantik), sehr häufig geschieht
dies jedoch informell.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Die Semantik maschinennaher Sprachen bezieht sich direkt auf real existierende Prozessoren:
 | Vorteil: Eine hohe Ausführungsgeschwindigkeit ist
möglich, wenn mit entsprechend viel Aufwand alle
Eigenheiten einer Maschine ausgenutzt und berücksichtigt
werden.
|
 | Nachteil: Maschinenprogramme werden bei einem
größeren Umfang sehr schnell unübersichtlich und
damit sehr fehleranfällig.
|
 | Noch ein Nachteil: Maschinennahe Programme funktionieren
nur auf Maschinen eines Typs und können nur unter
unverhältnismäßigem Aufwand auf andere Architekturen
portiert werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Höhere Programmiersprachen werden typischerweise mit einer Reihe von Zielsetzungen entwickelt:
 | Sie sollen für Menschen leichter lesbar, schreibbar
und wartbar sein.
|
 | Sie sollen unabhängig von einer konkreten Maschinenarchitektur
sein.
|
 | Es sollte möglich sein, Programmtexte in effiziente
Maschinenprogramme automatisch zu übersetzen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Anzahl der Seiten der Referenzdokumentationen ausgewählter
Programmiersprachen:
| ||||||||||||||||||||||||
 | ``The most important decision in language design concerns
what is to be left out.''
Niklaus Wirth, Autor von Pascal, Modula-2 und Oberon.
| ||||||||||||||||||||||||
 | ``Small is beautiful. Small is powerful. Small is easy
to understand.''
Guy L. Steele Jr., in seinem Vorwort zu einem Buch über Scheme.
| ||||||||||||||||||||||||
 | ``And to the minimalists in the crowd, Perl seems like a
pointless exercise in redundancy. But that's okay.
The world needs a few reductionists (mainly as physicists).
Reductionists like to take things apart.
The rest of us are just trying to get it together.''
Larry Wall, in seinem Vorwort zu ``Programming Perl''.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Im Normalfall werden Programmtexte durch einen
Übersetzer für die verwendete Programmiersprache
in die gewünschte Maschinensprache übersetzt.
|
 | Ein Übersetzer (auch Compiler genannt) unterstützt
dabei typischerweise genau eine Programmiersprache und
eine Zielarchitektur.
|
 | Es gibt auch Übersetzer, die Programmtexte in
andere Programmiersprachen oder in Maschinensprachen
für virtuelle Maschinen übersetzen.
|
 | Programme für virtuelle Maschinen können mit
Simulatoren zur Ausführung gebracht werden. Nachteil:
Simulatoren sind deutlich langsamer als reale Prozessoren.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Oberon als Programmiersprache wurde von Niklaus Wirth
(ETH Zürich) im Rahmen des gleichnamigen Projekts
Ende der 80er Jahre entwickelt. Zuvor war Niklaus Wirth
u.a. bereits bekannt für Pascal und Modula-2.
| ||||||
 | Oberon vereinigt drei wichtige Vorzüge:
| ||||||
 | Die Sprachdefinition ist unter http://www.mathematik.uni-ulm.de/oberon/reports/report-1992.html zu finden. | ||||||
 | Es gibt einige Varianten zu Oberon. Unter http://www.mathematik.uni-ulm.de/oberon/reports/ulmdiff-1994.html finden sich genaue Hinweise zu der von uns unterstützten Sprachversion. | ||||||
 | Dokumentation zu den Ulmer Oberon-Systemen finden sich unter http://www.mathematik.uni-ulm.de/oberon/ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
DEFINITION Hallo; END Hallo. |
(* Ausgabe einer kleinen Begruessungszeile
Andreas Borchert, 9. November 2004
*)
MODULE Hallo;
IMPORT Write;
BEGIN
Write.Line("Hallo, wie geht es?");
END Hallo.
|
 | Ein Oberon-Programm setzt sich aus vielen Modulen zusammen.
|
 | Zu jedem Modul gibt es zwei Programmtexte:
Eine Schnittstellendefinition, die beschreibt, was ein Modul
anderen Modulen zur Verfügung steht und das eigentliche
Modul.
|
 | Jeder Programmtext wird in einer eigenen Datei abgelegt.
|
 | Beim Ulmer Oberon-System werden die Dateien nach den
Modulen benannt, gefolgt von ``.od'' bei Schnittstellendefinitionen
und ``.om'' bei den eigentlichen Modulen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
doolin$ ls Hallo.od Hallo.om doolin$ oc Hallo.od doolin$ ls Hallo.od Hallo.om Hallo.sy doolin$ oc -c Hallo.om doolin$ ls Hallo.o Hallo.od Hallo.om Hallo.r Hallo.sy doolin$ oc -o Hallo Hallo.o doolin$ ls Hallo Hallo.o Hallo.od Hallo.om Hallo.r Hallo.sy doolin$ Hallo Hallo, wie geht es? doolin$ |
 | Auf unseren Suns steht der Oberon-Übersetzer über
das Kommando oc zur Verfügung.
|
 | Die Schnittstelle (hier ``Hello.od'') muß zuerst
übersetzt werden. Es entsteht dabei die sogenannte
Symboldatei ``Hello.sy''.
|
 | Danach kann das eigentliche Modul (hier ``Hello.om'')
übersetzt werden. Dabei entsteht ``Hello.o'', das
den Maschinen-Code enthält, und ``Hello.r'', das bei
einer späteren Fehleranalyse behilflich sein kann.
|
 | Schließlich kann das fertige ausführbare Programm
gebaut werden unter Verwendung der Bibliothek (hier wurde
konkret das Modul ``Write'' verwendet).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
doolin$ mmo -c Makefile doolin$ ls Hallo.od Hallo.om Makefile doolin$ make oc -c -u Hallo.od Hallo.om oc -o Hallo \ Hallo.o doolin$ Hallo Hallo, wie geht es? doolin$ make realclean rm -f Hallo.sy Hallo.r Hallo.o *.ts core rm -f Hallo doolin$ ls Hallo.od Hallo.om Makefile doolin$ |
 | make ist ein Werkzeug, das gewünschte Dateien
entsprechend eines Abhängigkeitsgraphen und eines Regelwerkes
mit minimalem Aufwand baut. Voraussetzung dafür ist ein
sogenanntes Makefile, das die Abhängigkeiten beschreibt.
|
 | Für Oberon kann ein Makefile mit mmo
(make makefile for Oberon) automatisch erzeugt werden.
|
 | Danach genügt ein Aufruf von make, um das
ausführbare Programm zu erzeugen.
|
 | Mit make realclean können alle generierbaren
Dateien wieder gelöscht werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
archimedes$ ls Hallo.od Hallo.om archimedes$ obci Hallo.od Hallo.om archimedes$ ls Hallo.od Hallo.om archimedes$ obbuild Hallo archimedes$ ls Hallo Hallo.od Hallo.om archimedes$ Hallo Hallo, wie geht es? archimedes$ |
 | Wenn Sie das Ulmer Oberon-System unter Linux verwenden,
erfolgen die Übersetzungen mit Hilfe einer Datenbank.
|
 | Mit obci (Oberon check-in) laden Sie die
angegebenen Quellen in die Datenbank.
|
 | Mit obbuild wird mit Hilfe der Module aus der
Datenbank ein ausführbares Programm generiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
DEFINITION Hallo; END Hallo. |
 | Programmtexte sind zunächst endliche Sequenzen aus Zeichen.
|
 | Traditionellerweise werden nur sogenannte ASCII-Zeichen
mit Nummern aus dem Bereich von 32 bis 126 verwendet. Hinzu
kommen nur noch Leerzeichen und Zeilentrenner.
|
 | Umlaute und andere spezielle Schriftzeichen werden vermieden,
da Programmtexte möglichst problemlos international lesbar und
verarbeitbar sein sollten.
|
 | Einzelne Zeichenfolgen werden (in Abhängigkeit von der jeweiligen
Programmiersprache) zu sogenannten lexikalischen Symbolen
zusammengefaßt.
|
 | Der Programmtext aus ``Hallo.od'' besteht aus sechs Symbolen:
``DEFINITION'', ``Hallo'', ``;'', ``END'', ``Hallo'' und ``.''.
|
 | Zwischen den Symbolen können und gelegentlich müssen auch
Leerzeichen und/oder Zeilentrenner stehen.
|
 | Würde das Leerzeichen zwischen ``DEFINITION'' und ``Hallo''
fehlen, würde daraus ein Symbol ``DEFINITIONHallo''.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
In Oberon gibt es eine Reihe lexikalischer Symbole:
 | Die Schlüsselwörter bestehen nur aus Großbuchstaben und
sind alle vordefiniert. Beispiele: ``DEFINITION'', ``END'',
``MODULE'', ``IMPORT'', ``BEGIN'' und ``END''.
|
 | Selbst definierte Namen dürfen frei gewählt werden, solange
sie nicht mit Schlüsselwörtern und anderen Namen kollidieren.
Sie müssen mit einem Buchstaben (``a'' bis ``z'' und ``A'' bis ``Z'')
beginnen und bestehen dann aus einer Folge von weiteren Buchstaben
und Ziffern. Zeichen wie ``-'', ``\_'' oder Umlaute sind nicht
zulässig. Der Unterschied zwischen Klein- und Großbuchstaben
ist signifikant. Beispiele: ``Hallo'', ``Write'', ``Line''. |
 | Interpunktionszeichen bestehen aus einem oder mehreren
speziellen Zeichen. Beispiele: ``;'', ``.'', ``('' und ``)''.
|
 | Zeichenketten bestehen aus einem doppelten Anführungszeichen,
einer beliebigen Zeichenfolge (ohne Zeilentrenner) und einem
weiteren doppelten Anführungszeichen. Beispiel: "Hallo, wie geht es?" |
 | Kommentare bestehen aus ``(*'', gefolgt von einem beliebigen Text
über beliebig viele Zeilen, der durch ``*)'' beendet wird.
Sie sind äquivalent zu Leerzeichen und dienen somit auch als
Trenner lexikalischer Symbole.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
archimedes$ cat Hallo.om
MODULE Hallo
IMPORT Write;
BEGIN
Write.Line("Hallo, wie geht es?");
END Hallo.
archimedes$ obci Hallo.om
archimedes$ obbuild Hallo
errors in MODULE Hallo:
1 MODULE Hallo
3 IMPORT Write;
** ";" is missing
obload: error: module Hallo: unable to load object
module Hallo: unable to load object
module Hallo: compilation failed
archimedes$
|
 | Nicht alle Sequenzen von lexikalischen Symbolen sind
zulässig.
|
 | Im obigen Beispiel fehlt das Semikolon hinter dem
Modulnamen und entsprechend wird die Übersetzung verweigert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Hallo2 ;IMPORT Write ;BEGIN Write . Line ( "Hallo, wie geht es?" ) ;END Hallo2 . |
 | Im Vordergrund steht die Lesbarkeit des Programmtexts
für den Entwickler und nicht für den Übersetzer.
|
 | Deswegen ist die disziplinierte Verwendung eines auf
Lesbarkeit ausgerichteten Stils essentiell.
|
 | Schopenhauer: ``Wer nachlässigt schreibt, legt dadurch
zunächst das Bekenntnis ab, daß er selbst seinen Gedanken
keinen großen Wert beilegt!''
|
 | Nietzsche: ``Den Stil verbessern --- das heißt den Gedanken
verbessern und nichts weiter.''
|
 | L. Reiners: ``[...] der Kampf um den Ausdruck ist ein Kampf
um den Inhalt. Um einen Gedanken knapp und kristallklar zu
formulieren, muß man ihn bis zum Ende durchdacht haben; [...]
die Form ist der Prüfstein des Gehalts.''
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Hallo3;
IMPORT Write;
BEGIN
Write.Line("Hallo, wie geht es?");
Write.Line("Mir geht es gut, aber");
Write.Line("gleich ist es mit mir zu Ende!");
END Hallo3.
|
 | Eigentliche Module beginnen immer mit dem Schlüsselwort
``MODULE'', gefolgt von dem Modulnamen und einem Semikolon.
|
 | Mit ``IMPORT'' kann eine durch Kommata getrennte Liste
von Modulen angegeben werden, die dann später in dem
gleichen Programmtext verwendet werden können. Diese Liste
wird durch ein Semikolon terminiert.
|
 | Zwischen den Schlüsselwörtern ``BEGIN'' und ``END''
stehen beliebig viele durch Semikolon getrennte Anweisungen,
die in der gegebenen Reihenfolge ausgeführt werden.
|
 | Wenn ein Befehl aus einem fremden Modul ausgeführt
werden soll (hier der Befehl ``Line'' aus dem Modul
``Write''), dann wird der Name in einer sogenannten qualifizierten
Form angegeben: Modulname, gefolgt von einem Punkt,
gefolgt von dem Namen des Befehls.
|
 | Allerdings ersetzt in Oberon der Begriff Prozedur
den des Befehls.
|
 | Die Prozedur ``Write.Line'' gibt eine als Parameter
übergebene Zeichenkette aus und fügt noch einen Zeilentrenner
in der Ausgabe hinzu.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Zu (fast) allen Modulen der Oberon-Bibliothek gibt
es Manualseiten, die sich beispielsweise mit ``man Write''
abrufen lassen.
|
 | Im Web findet sich auch ein Gesamtüberblick unter http://www.mathematik.uni-ulm.de/oberon/0.5/lib/man/ |
 | Die Manualseiten und sämtliche Programmtexte (auch
Quellen genannt) finden sich auch allesamt in unserem
Oberon-Paket für Linux. Mehr Hinweise dazu gibt es unter http://www.mathematik.uni-ulm.de/sai/ws04/prog/ulm-oberon-i386/ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Es sei ein Vokabular VT gegeben das aus einer
endlichen Menge von lexikalischen Symbolen besteht.
(Lexikalische Symbole werden auch Terminal-Symbole genannt,
daher die Bezeichnung VT).
|
 | Die Menge VT* ist dann die Menge aller endlichen
Folgen aus Symbolen aus VT, einschließlich der leeren Folge.
|
 | Eine Sprache S auf Basis des Vokabulars VT ist dann
eine Teilmenge von VT*.
|
 | Problem: Wie kann die Menge S mit endlichem Aufwand
definiert werden, wenn S unendlich viele Folgen enthält?
|
 | Lösung: Es werden Grammatiken verwendet, die aus endlich vielen
Bauvorschriften (genannt Produktionen) bestehen, die rekursiv
jede Folge aus S konstruieren können.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionen sind Ersetzungsregeln in der Form
| |||
 | Auf der linken Seite steht genau ein sogenanntes
Nicht-Terminal-Symbol (hier ⟨ A ⟩ ∈ VN).
Es gilt: VT ∩ VN = Ø.
| |||
 | Die Nicht-Terminal-Symbole dienen als Bezeichnung
komplexerer ``Bauteile'', die aus kleineren Teilen
zusammengesetzt sind. Ihnen werden normalerweise Namen
gegeben, die das ``Bauteil'' beschreiben.
| |||
 | Die rechte Seite besteht aus einer Sequenz von Terminal
oder Non-Terminal-Symbolen: α ∈ V*.
Diese Sequenz kann auch die Länge 0 haben.
| |||
 | Griechische Buchstaben stehen für
Sequenzen von Symbolen aus V*.
| |||
 | ε steht für eine Folge der Länge 0.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Eine Grammatik G ist ein 4-Tupel (VT, VN, P, S):
 | VT ist die endliche Menge der lexikalischen Symbole
(Terminal-Symbole).
|
 | VN ist die endliche Menge der Nicht-Terminal-Symbole.
|
 | VT ∩ VN = Ø.
|
 | P repräsentiert die Produktionen und
ist eine endliche Teilmenge aus VN x V*.
|
 | Statt der Tupel-Notation
(⟨ A ⟩, α) ∈ P wird
die Ersetzungsregelform
⟨ A ⟩ ---> α
verwendet.
|
 | ∀ ⟨ A ⟩ ∈ VN: ∃ α: (⟨ A ⟩, α) ∈ P. (Für jedes Nicht-Terminal-Symbol gibt es mindestens eine Produktionsregel, bei der das Symbol auf der linken Seite verwendet wird). |
 | S ∈ VN ist das Startsymbol.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Gegeben sei eine Grammatik G = (VT, VN, P, S):
 | α produziert β direkt:
α -> β falls sich α und β folgendermaßen zusammensetzen
| ||||||
 | α produziert β:
α ->+ β falls es ω1, ω2, ..., ωn ∈ V* gibt, so daß
| ||||||
 | Satzform für eine Grammatik: Jede Folge α mit S ->* α für α ∈ V*, S Startsymbol. | ||||||
 | Satz für eine Grammatik: Jede Satzform α ∈ VT*. | ||||||
 | Sprache, erzeugt von einer Grammatik: Die Menge aller möglichen Sätze. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Verbale Beschreibung: Eine Gleitkommazahl besteht
aus einer nicht-leeren Folge von Ziffern, optional gefolgt von einem
Komma und einer weiteren nicht-leeren Folge von Ziffern.
| |||||||||||||||||||||||||||
 | VT = {``0'', ``1'', ``2'', ``3'', ``4'', ``5'', ``6'', ``7'', ``8'', ``9'', ``,''}
| |||||||||||||||||||||||||||
 | VN = {⟨ Gleitkommazahl ⟩,
⟨ Vorkommastellen ⟩,
⟨ Nachkommastellen ⟩,
⟨ Ziffernfolge ⟩,
⟨ Ziffer ⟩}
| |||||||||||||||||||||||||||
 | Produktionsregeln P:
| |||||||||||||||||||||||||||
 | Startsymbol S = ⟨ Gleitkommazahl ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Behauptung: ``12,3'' ist ein Satz.
| |||||||||||||||||||||||||||
 | Beweis durch die Angabe der entsprechenden Ableitung:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Durch die Ableitung ergibt sich eine hierarchische
Struktur, die graphisch dargestellt werden kann.
|
 | Grammatiken dienen nicht nur zur Klärung, ob eine
Folge aus VT zu Sprache gehört, sondern liefern auch
Erfolgsfalle auch eine Struktur.
|
 | Allerdings sind manche Grammatiken mehrdeutig, d.h.
sie bieten mehrere Ableitungen für einen Satz an.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | VT = {⟨ Zahl ⟩, ``+'', ``*''}
| ||||||||||||
 | VN = {⟨ Summe ⟩, ⟨ Produkt ⟩}
| ||||||||||||
 | Produktionsregeln P:
| ||||||||||||
 | Startsymbol S = ⟨ Summe ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Grammatiken können durch die Ableitungsstruktur festlegen,
welche Operanden ein Operator erhält.
|
 | In diesem konkreten Beispiel wird die Multiplikation
zuerst durchgeführt, bevor es zur Addition kommt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | 1960 wurde von John Backus und Peter Naur bei der Beschreibung
von Algol-60 zum ersten Male eine formale Grammatik für
eine Programmiersprache spezifiziert.
| ||||||
 | Bei der formalen Notation von Backus und Naur (kurz
BNF = Backus-Naur-Form genannt) kommt zur Verringerung
der Anzahl der Produktionsregeln noch ``|'' als
Alternativsymbol hinzu.
| ||||||
 | Die Kurzform
⟨ A ⟩ ---> α | β
ist dabei äquivalent zu
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Die erweiterte Backus-Naur-Form (EBNF) fügt weitere Notationen hinzu, um die Zahl der Produktionsregeln weiter reduzieren zu können:
 | Optionalität:
⟨ A ⟩ ---> α [ β ] γ
entspricht
| ||||||
 | Wiederholung (0 bis beliebig oft):
⟨ A ⟩ ---> α { β } γ
entspricht
| ||||||
 | Klammerung:
⟨ A ⟩ ---> α ( β | γ ) δ
entspricht
| ||||||
 | Durch die Verwendung von EBNF geht ein Teil der Struktur
verloren, die mit BNF noch zum Ausdruck kam.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | VT = {⟨ Symbol ⟩, ``--->'', ``|'', ``['', ``]'', ``{'', ``}'', ``('', ``)''}
| |||||||||||||||||||||||||||||||||
 | VN = {⟨ Produktionsregeln ⟩,
⟨ Produktionsregel ⟩,
⟨ Alternativen ⟩,
⟨ Sequenz ⟩,
⟨ Element ⟩}
| |||||||||||||||||||||||||||||||||
 | Produktionsregeln P:
| |||||||||||||||||||||||||||||||||
 | Startsymbol S = ⟨ Produktionsregeln ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | VT = {
``ARRAY'', ``BEGIN'', ``CASE'',
``CONST'', ``DEFINITION'',
``DIV'', ``DO'', ``ELSE'', ``ELSIF'', ``END'', ``EXIT'', ``FOR'', ``IF'', ``IMPORT'', ``IN'', ``IS'', ``LOOP'', ``MOD'', ``MODULE'', ``NIL'', ``OF'', ``OR'', ``POINTER'', ``PROCEDURE'', ``RECORD'', ``REPEAT'', ``RETURN'', ``THEN'', ``TO'', ``TYPE'', ``UNTIL'', ``VAR'', ``WHILE'', ``WITH'', ``+'', ``-'', ``*'', ``/'', ``˜'', ``&'', ``.'', ``,'', ``;'', ``|'', ``('', ``['', ``{'', ``:='', `` ^ '', ``='', ``#'', ``<'', ``>'', ``<='', ``>='', ``:'', ``)'', ``]'', ``}'', ``..'', ``:='', ``<='', ``>='', ⟨ CharConstant ⟩, ⟨ Ident ⟩, ⟨ Number ⟩, ⟨ String ⟩ } |
 | VN = {
⟨ ActualParameters ⟩,
⟨ AddOperator ⟩,
⟨ ArrayType ⟩,
⟨ Assignment ⟩, ⟨ BaseType ⟩, ⟨ CaseLabelList ⟩, ⟨ CaseLabels ⟩, ⟨ CaseStatement ⟩, ⟨ Case ⟩, ⟨ CompilationUnit ⟩, ⟨ ConstExpression ⟩, ⟨ ConstantDeclaration ⟩, ⟨ DeclarationSequence ⟩, ⟨ DefSequence ⟩, ⟨ Definition ⟩, ⟨ Designator ⟩, ⟨ Element ⟩, ⟨ ExpList ⟩, ⟨ Expression ⟩, ⟨ FPSection ⟩, ⟨ Factor ⟩, ⟨ FieldListSequence ⟩, ⟨ FieldList ⟩, ⟨ FormalParameters ⟩, ⟨ FormalType ⟩, ⟨ ForwardDeclaration ⟩, ⟨ IdentList ⟩, ⟨ IfStatement ⟩, ⟨ ImportList ⟩, ⟨ Import ⟩, ⟨ Length ⟩, ⟨ LoopStatement ⟩, ⟨ Module ⟩, ⟨ MulOperator ⟩, ⟨ PointerType ⟩, ⟨ ProcedureBody ⟩, ⟨ ProcedureCall ⟩, ⟨ ProcedureDeclaration ⟩, ⟨ ProcedureHeading ⟩, ⟨ ProcedureType ⟩, ⟨ QualIdent ⟩, ⟨ RecordType ⟩, ⟨ Relation ⟩, ⟨ RepeatStatement ⟩, ⟨ Set ⟩, ⟨ SimpleExpression ⟩, ⟨ StatementSequence ⟩, ⟨ Statement ⟩, ⟨ Term ⟩, ⟨ TypeDeclaration ⟩, ⟨ Type ⟩, ⟨ VariableDeclaration ⟩, ⟨ WhileStatement ⟩, ⟨ WithStatement ⟩ } |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Produktionsregeln P (in EBNF, Fortsetzung):
| ||||||||||||||||||||||||||||||||||||
 | Startsymbol S = ⟨ CompilationUnit ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Hallo;
IMPORT Write;
BEGIN
Write.Line("Hallo, wie geht es?");
END Hallo.
|
| ⟨ CompilationUnit ⟩ | ---> | ⟨ Module ⟩ |
| ---> | ``MODULE'' ⟨ Ident ⟩ ``;'' | |
| [⟨ ImportList ⟩] ⟨ DeclarationSequence ⟩ | ||
| [``BEGIN'' ⟨ StatementSequence ⟩] | ||
| ``END'' ⟨ Ident ⟩ ``.'' | ||
| ---> | ``MODULE'' ⟨ Ident ⟩ ``;'' ⟨ ImportList ⟩ | |
| ``BEGIN'' ⟨ StatementSequence ⟩ | ||
| ``END'' ⟨ Ident ⟩ ``.'' | ||
| ⟨ ImportList ⟩ | ---> | ``IMPORT'' ⟨ Import ⟩ |
| { ``,'' ⟨ Import ⟩ } ``;'' | ||
| ---> | ``IMPORT'' ⟨ Import ⟩ ``;'' | |
| ---> | ``IMPORT'' ⟨ Ident ⟩ [``:='' ⟨ Ident ⟩] ``;'' | |
| ---> | ``IMPORT'' ⟨ Ident ⟩ ``;'' | |
| ⟨ StatementSequence ⟩ | ---> | ⟨ Statement ⟩ { ``;'' ⟨ Statement ⟩ } |
| ---> | ⟨ Statement ⟩ | |
| ---> | ⟨ ProcedureCall ⟩ | |
| ---> | ⟨ Designator ⟩ [⟨ ActualParameters ⟩] | |
| ---> | ⟨ QualIdent ⟩ ⟨ ActualParameters ⟩ | |
| ---> | [⟨ Ident ⟩ ``.''] ⟨ Ident ⟩ ⟨ ActualParameters ⟩ | |
| ---> | ⟨ Ident ⟩ ``.'' ⟨ Ident ⟩ ⟨ ActualParameters ⟩ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Hallo;
IMPORT Write;
BEGIN
Write.Line("Hallo, wie geht es?");
END Hallo.
|
| ⟨ ActualParameters ⟩ | ---> | ``('' [⟨ ExpList ⟩] ``)'' |
| ---> | ``('' ⟨ ExpList ⟩ ``)'' | |
| ---> | ``('' ⟨ Expression ⟩ ``)'' | |
| ---> | ``('' ⟨ SimpleExpression ⟩ ``)'' | |
| ---> | ``('' ⟨ Term ⟩ ``)'' | |
| ---> | ``('' ⟨ Factor ⟩ ``)'' | |
| ---> | ``('' ⟨ String ⟩ ``)'' | |
| ⟨ CompilationUnit ⟩ | ---> | ``MODULE'' ⟨ Ident ⟩ ``;'' ⟨ ImportList ⟩ |
| ``BEGIN'' ⟨ StatementSequence ⟩ | ||
| ``END'' ⟨ Ident ⟩ ``.'' | ||
| ---> | ``MODULE'' ⟨ Ident ⟩ ``;'' | |
| ``IMPORT'' ⟨ Ident ⟩ ``;'' | ||
| ``BEGIN'' | ||
| ⟨ Ident ⟩ ``.'' ⟨ Ident ⟩ ``('' ⟨ String ⟩ ``)'' | ||
| ``END'' ⟨ Ident ⟩ ``.'' |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Variablen |
 | Beispiel: Summe zweier Zahlen |
 | Variablendeklarationen |
 | Einlesen von Variablen |
 | Zuweisung |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Speicherzellen stehen in beliebigem Umfange zur
Verfügung, soweit ausreichend Speicher und Adreßraum
vorhanden sind.
|
 | Anders als in Redcode oder anderen maschinennahen
Programmiersprachen bleibt dem Programmierer in Oberon
(weitgehend) verborgen, welche konkrete Adresse eine
Speicherzelle hat.
|
 | Statt über Adressen werden innerhalb von Oberon
Speicherzellen ausschließlich über Variablennamen
angesprochen.
|
 | Entsprechend wird in Oberon der Begriff Variable
für Speicherzellen verwendet.
|
 | Bei Redcode gab es keine unterschiedlichen Sorten
an Speicherzellen. Das ist in Oberon anders. Hier ist
jeder Variablen ein Typ zugeordnet.
|
 | Typische Typen sind beispielsweise ganze Zahlen
(INTEGER), Gleitkommazahlen (REAL) und
Zeichen (CHAR). Innerhalb von Oberon können
auch neue Typen definiert werden.
|
 | Die interne Repräsentierung einer Variablen wird
in Oberon nur entsprechend ihres Typs interpretiert.
|
 | Oberon hat ein sicheres Typsystem, d.h. eine
Variable vom Typ (INTEGER) kann nicht versehentlich
als Variable vom Typ (REAL) behandelt werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* Description: Read two integer values and print their sum
Author: Andreas Borchert
*)
MODULE Sum;
IMPORT Read, Write;
VAR
a, b: INTEGER; (* input values *)
sum: INTEGER; (* sum of a + b *)
BEGIN
(* read input values *)
Write.String("a = "); Read.Int(a);
Write.String("b = "); Read.Int(b);
sum := a + b;
(* print result *)
Write.String("sum = "); Write.Int(sum, 1); Write.Ln;
END Sum.
|
 | Variablendeklarationen beginnen mit dem Schlüsselwort VAR.
|
 | Variablennamen sollten immer mit einem
Kleinbuchstaben beginnen.
|
 | INTEGER ist ein vorgegebener Typ, der für eine ganze Zahl
steht. Bei uns kann dieser Typ Werte aus dem Intervall [-2147483648,2147483647] repräsentieren. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
VAR a, b: INTEGER; (* input values *) sum: INTEGER; (* sum of a + b *) |
 | Syntax für Variablendeklarationen:
| |||||||||||||||||||||
 | Im Beispiel werden drei Variablen, genannt a, b
und sum, vom Typ INTEGER deklariert.
| |||||||||||||||||||||
 | Unter Verwendung einer ⟨ IdentList ⟩
können gleich mehrere Variablen deklariert werden, ohne den
Typen jeweils wiederholen zu müssen. Diese Notation sollte
aber nur für eng zusammengehörende Variablen verwendet werden.
| |||||||||||||||||||||
 | Der Inhalt einer Variablen ist zu Beginn nicht definiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* read input values *)
Write.String("a = "); Read.Int(a);
Write.String("b = "); Read.Int(b);
|
 | Anweisungen (in der Oberon-Grammatik
⟨ Statement ⟩ genannt) werden in Oberon durch
Semikolon voneinander getrennt: ⟨ StatementSequence ⟩ ---> ⟨ Statement ⟩ { ``;'' ⟨ Statement ⟩ } | ||||||
 | Write.String gibt eine Zeichenkette ohne Zeilentrenner
aus.
| ||||||
 | Read.Int liest eine ganze Zahl ein und legt speichert
sie im Erfolgsfalle in der angegebenen Variablen, die vom
Typ INTEGER sein muß.
| ||||||
 | Beim Einlesen von einem Terminal gelten folgende Regeln:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
sum := a + b; |
 | Zuweisungen entsprechen der MOV-Anweisung in Redcode,
bei der ein Wert von einer Speicherzelle in eine andere kopiert
worden ist.
|
 | In Oberon kann der zu kopierende Wert zuerst mit einem
Ausdruck berechnet werden.
|
 | Eine Zuweisung besteht aus dem Ziel (in der Oberon-Grammatik
⟨ Designator ⟩ genannt), der Sequenz
``:='' und einem Ausdruck: ⟨ Assignment ⟩ ---> ⟨ Designator ⟩ ``:='' ⟨ Expression ⟩ |
 | Im einfachsten Falle kann für
⟨ Designator ⟩
der Name einer Variablen eingesetzt werden.
|
 | Wenn in einem Ausdruck Variablen verwendet werden, sollte
sichergestellt sein, daß diese zuvor initialisiert worden sind.
In diesem konkreten Falle geschah dies durch die beiden
Aufrufe von Read.Int. Wenn dies fehlt, sind die Werte
undefiniert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
|
 | Mit der IF-Anweisung wird aufgrund von einer Bedingung
entschieden, welche weiteren Anweisungen zur Ausführung gelangen.
| |||||||||||||
 | Syntax:
| |||||||||||||
 | < ist ein Vergleichsoperator, der auf eine Reihe
von Typen angewendet werden kann (z.B. auf INTEGER).
| |||||||||||||
 | Das Resultat ist vom Typ BOOLEAN. Bei diesem
Typ gibt es nur zwei mögliche Werte: TRUE und FALSE.
| |||||||||||||
 | Die IF-Anweisung erwartet bei ihrer Bedingung einen
beliebigen Ausdruck vom Typ BOOLEAN.
| |||||||||||||
 | Ist der Wert der Bedingung TRUE, wird der
THEN-Teil ausgeführt, ansonsten der ELSE-Teil.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004 Andreas Borchert, in HTML konvertiert am 14.11.2004 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
Write.String("Your guess: "); Read.LongInt(guess);
WHILE guess # secretNumber DO
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
Write.String("Your guess: "); Read.LongInt(guess);
END;
|
 | Syntax:
| |||||||
 | Bei einer WHILE-Schleife wird zunächst die
Bedingung ausgewertet. Falls sie TRUE ist,
werden die Anweisungen innerhalb der Schleife ausgeführt
und danach wird die Bedingung erneut überprüft.
Die Anweisungen innerhalb der Schleife werden solange
wiederholt, bis die Bedingung FALSE wird. Danach
geht die Ausführung hinter der WHILE-Anweisung
weiter.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004 Andreas Borchert, in HTML konvertiert am 14.11.2004 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
MODULE Hilo;
IMPORT RandomGenerators, Read, Write;
VAR
secretNumber: LONGINT;
(* secret number out of [1..1024] *)
guess: LONGINT; (* last guess *)
BEGIN
secretNumber := RandomGenerators.Val(1, 1024);
Write.Line("Welcome to the Hilo game!");
Write.String("Please guess the secret number ");
Write.Line("out of [1..1024]");
Write.String("Your guess: "); Read.LongInt(guess);
WHILE guess # secretNumber DO
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
Write.String("Your guess: "); Read.LongInt(guess);
END;
Write.String("Congratulations, ");
Write.Line("you found the secret number!");
END Hilo.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004 Andreas Borchert, in HTML konvertiert am 14.11.2004 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
|
VAR secretNumber: LONGINT; (* secret number out of [1..1024] *) guess: LONGINT; (* last guess *) |
 | Die Variablen secretNumber und guess
sind vom Typ LONGINT. LONGINT umfaßt
unserer Implementierung den gleichen Bereich wie INTEGER.
Die Verwendung von LONGINT ist hier notwendig, da
RandomGenerators.Val einen Wert vom Typ LONGINT
liefert.
|
 | RandomGenerators.Val ist eine Funktion, die eine
pseudo-zufällige Zahl aus dem angegebenen Bereich liefert.
Diese Zahl wird in einer Zuweisung der Variablen
secretNumber zugewiesen.
|
secretNumber := RandomGenerators.Val(1, 1024); |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
|
| Copyright © 2004 Andreas Borchert, in HTML konvertiert am 14.11.2004 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Kontrollstrukturen |
 | Bedingte Verzweigungen |
 | WHILE-Schleife |
 | Beispiel: Hilo-Spiel |
 | Beispiel: Hilo-Spiel II |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Bislang wurden alle Anweisungen linear in der Reihenfolge
ausgeführt, in der sie im Programmtext standen.
|
 | Kontrollstrukturen sind Anweisungen, die Wiederholungen
und bedingte Verzweigungen im Programmtext ermöglichen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
|
 | Mit der IF-Anweisung wird aufgrund von einer Bedingung
entschieden, welche weiteren Anweisungen zur Ausführung gelangen.
| ||||||||||||||||||
 | Syntax:
| ||||||||||||||||||
 | < ist ein Vergleichsoperator, der auf eine Reihe
von Typen angewendet werden kann (z.B. auf INTEGER).
| ||||||||||||||||||
 | Das Resultat ist vom Typ BOOLEAN. Bei diesem
Typ gibt es nur zwei mögliche Werte: TRUE und FALSE.
| ||||||||||||||||||
 | Die IF-Anweisung erwartet bei ihrer Bedingung einen
beliebigen Ausdruck vom Typ BOOLEAN.
| ||||||||||||||||||
 | Ist der Wert der Bedingung TRUE, wird der
THEN-Teil ausgeführt, ansonsten der ELSE-Teil.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Write.String("Your guess: "); Read.LongInt(guess);
WHILE guess # secretNumber DO
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
Write.String("Your guess: "); Read.LongInt(guess);
END;
|
 | Syntax:
| |||||||||
 | Bei einer WHILE-Schleife wird zunächst die
Bedingung ausgewertet. Falls sie TRUE ist,
werden die Anweisungen innerhalb der Schleife ausgeführt
und danach wird die Bedingung erneut überprüft.
Die Anweisungen innerhalb der Schleife werden solange
wiederholt, bis die Bedingung FALSE wird. Danach
geht die Ausführung hinter der WHILE-Anweisung
weiter.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Hilo;
IMPORT RandomGenerators, Read, Write;
VAR
secretNumber: LONGINT;
(* secret number out of [1..1024] *)
guess: LONGINT; (* last guess *)
BEGIN
secretNumber := RandomGenerators.Val(1, 1024);
Write.Line("Welcome to the Hilo game!");
Write.String("Please guess the secret number ");
Write.Line("out of [1..1024]");
Write.String("Your guess: "); Read.LongInt(guess);
WHILE guess # secretNumber DO
IF guess < secretNumber THEN
Write.Line("Too small!");
ELSE
Write.Line("Too large!");
END;
Write.String("Your guess: "); Read.LongInt(guess);
END;
Write.String("Congratulations, ");
Write.Line("you found the secret number!");
END Hilo.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
VAR secretNumber: LONGINT; (* secret number out of [1..1024] *) guess: LONGINT; (* last guess *) |
 | Die Variablen secretNumber und guess
sind vom Typ LONGINT. LONGINT umfaßt
unserer Implementierung den gleichen Bereich wie INTEGER.
Die Verwendung von LONGINT ist hier notwendig, da
RandomGenerators.Val einen Wert vom Typ LONGINT
liefert.
|
 | RandomGenerators.Val ist eine Funktion, die eine
pseudo-zufällige Zahl aus dem angegebenen Bereich liefert.
Diese Zahl wird in einer Zuweisung der Variablen
secretNumber zugewiesen.
|
secretNumber := RandomGenerators.Val(1, 1024); |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Ein erstes Beispiel mit Oberon |
 | Struktur eines Programmtextes |
 | Ableitungsbeispiel für Oberon |
 | Ableitungsbeispiel für Oberon II |
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Beispiel: Summe zweier Zahlen |
 | Variablendeklarationen |
 | Einlesen von Variablen |
 | Zuweisung |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Bedingte Verzweigungen |
 | WHILE-Schleife |
 | Beispiel: Hilo-Spiel |
 | Beispiel: Hilo-Spiel II |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Ein deterministischer endlicher Automat A ist ein 5-Tupel (Z, V, δ, s, E):
 | Z ist eine endliche Menge von Zuständen.
|
 | V ist eine endliche Menge von Symbolen.
|
 | δ ist eine Übergangsfunktion
δ: Z x V -> Z.
|
 | s ∈ Z ist der Startzustand.
|
 | E ⊆ Z ist die Menge der zulässigen Endzustände.
|
Wenn eine Zeichenfolge α = (α1, ···, αn) ∈ V* (n >= 0) gegeben ist, ergibt sich entsprechend eine Folge von Zuständen ζ mit
| ζ0 | = | s |
| ζi | = | δ(ζi-1, αi) (i >= 1) |
Ein endlicher Automat A erkennt die Zeichenfolge α ∈ V*, falls gilt: ζn ∈ E.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Z = {z1, ···, z5}
| ||||||||||||||||||||||||
 | V = {``0'', ···, ``9'', ``,''}
| ||||||||||||||||||||||||
 |
| ||||||||||||||||||||||||
 | s = z1
| ||||||||||||||||||||||||
 | E = {z2, z4}
| ||||||||||||||||||||||||
Hinweis: z5 dient als Fehlerzustand. Wenn an einer unpassenden Stelle ein Komma kommt (z.B. zu Beginn oder nachdem bereits ein Komma gesehen worden ist), dann bleibt der Automat bis zum Ende der Eingabefolge in diesem Fehlerzustand.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Jeder Zustand aus Z wird durch einen Kreis repräsentiert.
|
 | Sei Vi,j die Menge aller v ∈ V für die
gilt: δ(zi, v) = zj. Falls Vi,j ≠ Ø,
dann ist ein gerichteter Pfeil zu zeichnen von dem Kreis
für zi zu dem Kreis von zj, der mit der Menge Vi,j
beschriftet wird.
|
 | Der Anfangszustand z1 wird durch ein ``S'' markiert.
|
 | Zulässige Endzustände werden durch einen doppelten Kreis markiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE FloatingPointAutomaton;
IMPORT ASCII, Read, Write;
VAR state: INTEGER; symbol: CHAR;
BEGIN
state := 1; (* initial state *)
Read.Char(symbol);
WHILE symbol # ASCII.nl DO
CASE symbol OF
| "0".."9":
CASE state OF
| 1: state := 2;
| 2: state := 2;
| 3: state := 4;
| 4: state := 4;
| 5: state := 5;
END;
| ",":
CASE state OF
| 1: state := 5;
| 2: state := 3;
| 3: state := 5;
| 4: state := 5;
| 5: state := 5;
END;
ELSE
state := 5;
END;
Read.Char(symbol);
END;
CASE state OF
| 2, 4: Write.Line("Looks good!");
ELSE Write.Line("Invalid input!");
END;
END FloatingPointAutomaton.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
VAR symbol: CHAR; (* current input symbol *) |
 | CHAR repräsentiert ein einzelnes Zeichen in Oberon.
|
 | Als Repräsentierung stehen nur 8 Bit zur Verfügung,
die entsprechend ASCII belegt sind (Werte 0 bis 127).
Der Bereich aus 128 bis 255 unterliegt den jeweils lokalen
Konventionen (bei uns beispielsweise ISO-8859-1).
|
Read.Char(symbol); WHILE symbol # ASCII.nl DO (* ... *) Read.Char(symbol); END; |
 | Mit Read.Char wird das nächste Zeichen aus der
Eingabe in die angegebene Variable abgespeichert.
|
 | ASCII.nl ist das Zeichen, das den Zeilentrenner
repräsentiert.
|
 | Die WHILE-Schleife wiederholt ihre inneren
Anweisungen solange, bis ein Zeilentrenner eingelesen wird.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CASE symbol OF | "0".."9": CASE state OF | 1: state := 2; | 2: state := 2; | 3: state := 4; | 4: state := 4; | 5: state := 5; END; | ",": CASE state OF | 1: state := 5; | 2: state := 3; | 3: state := 5; | 4: state := 5; | 5: state := 5; END; ELSE (* enter error state in case of unknown symbols *) state := 5; END; |
 | Bei einer CASE-Anweisung wird zunächst der
Ausdruck hinter dem CASE-Schlüsselwort berechnet.
|
 | Danach wird untersucht, ob dieser Wert einem der
angegebenen Fälle entspricht. Falls ja, wird der
zugehörige Programmtext ausgeführt.
|
 | Bei den einzelnen Fällen können beliebig viele
durch Kommata getrennte Konstanten aufgezählt werden.
Auch Bereichsangaben sind unter Verwendung von ..
zulässig.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CASE state OF | 1: state := 2; | 2: state := 2; | 3: state := 4; | 4: state := 4; | 5: state := 5; END; |
 | Trifft keiner der angegebenen Fälle zu, wird
der ELSE-Fall verwendet. Fehlt der ELSE-Fall,
stürzt das Programm (kontrolliert) ab.
| |||||||||||||||||||||
 | Das ist in vielen Fällen wünschenswert, da es auf
diese Weise auffällt, daß irgendeine Variable einen
unerwarteten Wert hat.
| |||||||||||||||||||||
 | Syntax:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Sprachen, die mit einem endlichen Automaten definiert werden können, werden reguläre Sprachen genannt. Die entsprechende Grammatik läßt sich mit folgendem Verfahren ableiten:
 | VT = V (die Menge der Terminal-Symbole der Grammatik
entspricht genau der Menge der Symbole des Automaten)
|
 | VN = Z (aus jedem Zustand des Automaten wird je ein
Nicht-Terminal-Symbol der Grammatik)
|
 | Für jeden Zustand z ∈ E (Endzustand) gibt
es eine Produktionsregel: ⟨ z ⟩ ---> ε |
 | Für alle Zustandskombinationen (zi,zj) ∈ Z x Z,
wird für jedes Symbol v aus Vi,j eine Produktionsregel
gebildet: ⟨ zi ⟩ ---> v ⟨ zj ⟩ |
 | S = ⟨ s ⟩ (das Startsymbol des Automaten
wird zum Startsymbol der Grammatik)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Der endliche Automat für Gleitkommazahlen läßt sich in entsprechend der vorgestellten Transformationsregel in eine Grammatik überführen:
 | VT = {``0'', ···, ``9'', ``,''}
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | VN = {⟨ z1 ⟩, ···, ⟨ z5 ⟩}
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | Produktionsregeln P:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = ⟨ z1 ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Können alle durch Grammatiken beschreibbare Sprachen auch durch endliche Automaten beschrieben werden?
Hier ist eine Grammatik für eine Sprache, für die kein endlicher Automat gefunden werden kann:
 | VT = {``('', ``)''}
| |||||||||
 | VN = {⟨ A ⟩, ⟨ B ⟩}
| |||||||||
 | Produktionsregeln P:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die LOOP-Anweisung ist die einfachste und gleichzeitig
flexibelste Schleife.
| ||||||||||||||||||
 | Sie wird von den Schlüsselwörtern LOOP und END
umrahmt.
| ||||||||||||||||||
 | Die EXIT-Anweisung verläßt die innerste die
EXIT-Anweisung umgebende LOOP-Schleife und
setzt die Ausführung unmittelbar hinter dem END fort.
| ||||||||||||||||||
 | Beliebig viele EXIT-Anweisungen sind innerhalb
einer LOOP-Schleife zulässig.
| ||||||||||||||||||
 | EXIT ist außerhalb einer LOOP-Anweisung
nicht zulässig, obwohl es die Oberon-Grammatik zulassen würde.
| ||||||||||||||||||
 | Syntax:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 |
WHILE Bedingung DO ist (nahezu) äquivalent zu
LOOP |
 | Der Operator ~ steht dabei für die logische Negation,
d.h. TRUE wird zu FALSE abgebildet und FALSE
zu TRUE.
|
 | Das ``nahezu'' bezieht sich darauf, daß eine
WHILE-Anweisung für EXIT-Anweisungen irrelevant
ist, eine LOOP-Anweisung hingegen schon.
|
 | Es gibt auch eine elegantere Fassung im Vergleich zur
LOOP-Anweisung, wenn die Bedingung am Ende geprüft
werden soll:
REPEAT ist (nahezu) äquivalent zu
LOOP |
 | Achtung: Bei UNTIL gibt die Bedingung an, wann
die Schleife zu beenden ist, bei WHILE gibt die Bedingung
an, wann die Schleife fortzusetzen ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* read integers from standard input and print minimal value *) MODULE Minimum; IMPORT Read, Streams, Write; VAR min: INTEGER; (* minimal value seen so far *) mindefined: BOOLEAN; (* min well-defined? *) value: INTEGER; (* last input value *) BEGIN mindefined := FALSE; (* min not initialized yet *) LOOP Read.Int(value); (* try to read a value *) IF Streams.stdin.count = 0 THEN EXIT END; (* value is well-defined now *) IF ~mindefined OR (value < min) THEN (* new minimum found *) min := value; mindefined := TRUE; END; END; IF mindefined THEN Write.Int(min, 1); Write.Ln; END; END Minimum. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
LOOP Read.Int(value); (* try to read a value *) IF Streams.stdin.count = 0 THEN EXIT END; (* value is well-defined now *) IF ~mindefined OR (value < min) THEN (* new minimum found *) min := value; mindefined := TRUE; END; END; |
 | Lese-Operationen wie Read.Int können wie erhofft
funktionieren oder auch fehlschlagen.
|
 | Ein Read.Int schlägt beispielsweise fehl, wenn
die Eingabe beendet ist oder ein Buchstabe anstatt einer
Ziffernfolge eingegeben wird.
|
 | Die externe Variable Streams.stdin.count ist
vom Typ INTEGER und ist 0, falls die letzte Einlese-Operation
von der Standard-Eingabe (Streams.stdin) nicht
erfolgreich war --- aus welchem Grunde auch immer.
Andernfalls ist sie positiv.
|
 | Wenn der Erfolg von Lese-Operationen überprüft werden
soll, ist folgender genereller Schleifenaufbau sinnvoll:
LOOP |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Alternativ zu LOOP gibt es natürlich auch Varianten auf Basis der anderen Schleifen-Anweisungen:
 |
Leseoperation
Nachteil: Die Leseoperation muß an zwei Stellen angegeben
werden. Dieser Nachteil kann aber in manchen Fällen eliminiert
werden, wenn das Einlesen innerhalb der Schleifenbedingung
erfolgen kann. (Das wurde jedoch noch nicht vorgestellt).
|
 |
REPEAT
Nachteil: Der Erfolg der Lese-Operation wird an zwei Stellen
überprüft.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Spätestens, wenn zusätzliche Tests der Eingabedaten
erfolgen, sollte jedoch eine LOOP-Schleife
bevorzugt werden.
|
 | Typisches Schema mit der Möglichkeit einer erneuten
Eingabe:
LOOP |
 | Schema ohne die Möglichkeit einer erneuten Eingabe:
LOOP |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | In Oberon (und vielen anderen Programmiersprachen) wird
zunächst ein Einlese-Versuch gestartet und dann wird
getestet, ob dieser erfolgreich war.
|
 | Es ist nicht sinnvoll, diese Reihenfolge umzudrehen.
da die Statusvariablen unterhalb von Streams.stdin
den Erfolg oder Mißerfolg des letzten Einlese-Versuches
widerspiegeln.
|
 | Es gibt einige Programmiersprachen (wie z.B. Pascal),
die es erlauben, zuerst zu testen und dann zu lesen:
WHILE NOT EOF DO BEGIN
Dieses Schema sollte nicht nach Oberon übertragen werden!
(Anders als in Oberon impliziert der EOF-Test in
Pascal eine Lese-Operation, falls der Eingabe-Puffer momentan
leer ist. In Oberon führen die Tests niemals implizit zu
Ein- oder Ausgabe-Operationen).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Es gibt endliche Automaten, die Ausgabetext produzieren in Abhängigkeit
 | von dem aktuellen Zustand: Moore-Maschine.
|
 | von dem aktuellen Zustand und dem nächsten
Eingabe-Symbol: Mealy-Maschine.
|
In Ergänzung oder an Stelle der Ausgabe sind natürlich auch beliebige andere Anweisungen denkbar, die einen Zustand außerhalb den des Automaten manipulieren. Endliche Automaten als Grundstruktur sind vielfach in Gebrauch in der Kommunikation mit anderen Programmen (z.B. über ein Netzwerk) oder mit Hardware.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
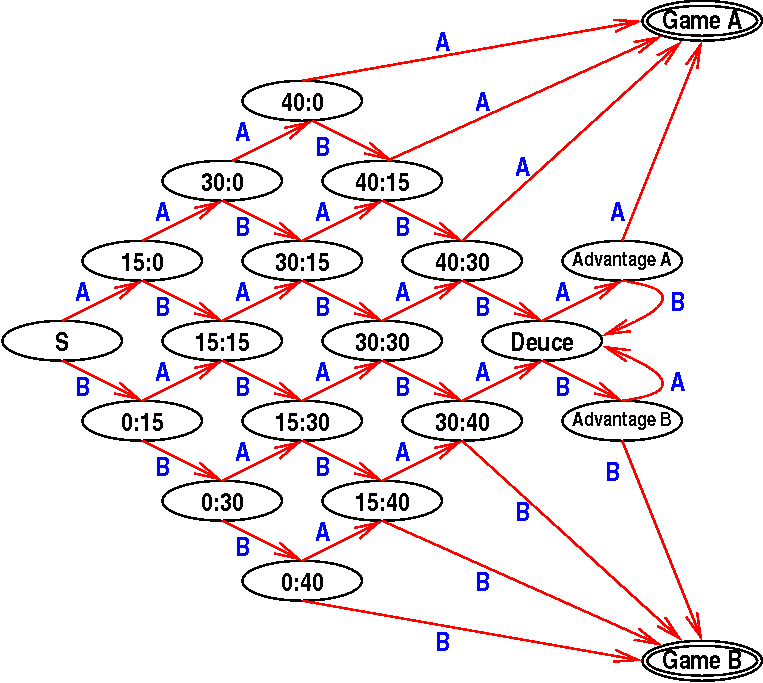
 | Ein Tennis-Spiel strukturiert sich hierarchisch
in ein Match, das aus mehreren Sätzen besteht, die
wiederum aus Spielen zusammengesetzt sind, die aus
einer Reihe von Punkten bestehen.
|
 | Das Diagramm zeigt einen Moore-Automaten für ein
einzelnes Tennis-Spiel.
|
 | V = {``A'', ``B''} (``A'' heißt ein Punkt ging an Spieler A, ``B'' weist entsprechend einen gewonnen Punkt an Spieler B zu). |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Tennis;
IMPORT ASCII, Read, Streams, Write;
(* ... CONST definitions ... *)
VAR
state: INTEGER; (* current state *)
ch: CHAR; (* last input character *)
BEGIN
Write.Line("A vs B");
state := s0to0; (* initial state *)
LOOP (* until game is finished or no input is available *)
(* print current state *)
(* store next valid input character into ch;
set ch to 0X (null-byte) if no valid input
is available
*)
(* compute next state *)
END;
END Tennis.
|
 | Beim Durchlaufen der LOOP-Anweisung
wird zunächst der aktuelle Zustand ausgegeben
(wie bei Moore-Automaten üblich), dann wird
das nächste Symbol gelesen und dann wird
der Folgezustand bestimmt.
|
 | Die LOOP-Schleife wird hier verlassen,
sobald einer der Endezustände erreicht wird
(geschieht bei der Ausgabe des Zustands) oder
ein weiteres Symbol nicht mehr eingelesen werden kann.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CONST (* states *) s0to0 = 0; s30to30 = 10; s0to15 = 1; s30to40 = 11; s0to30 = 2; s40to0 = 12; s0to40 = 3; s40to15 = 13; s15to0 = 4; s40to30 = 14; s15to15 = 5; deuce = 15; s15to30 = 6; advantageA = 16; s15to40 = 7; advantageB = 17; s30to0 = 8; gameA = 18; s30to15 = 9; gameB = 19; |
 | Die reine Verwendung von Zustandsnummern ist
wenig anschaulich und führt dazu, daß Verwechslungen
leicht übersehen werden.
| |||
 | Mit CONST können ``sprechende'' Namen für
Konstanten vereinbart werden. Die Namen können später
überall verwendet werden, wo die Verwendung einer
entsprechenden Konstante zulässig wäre.
| |||
 | Syntax:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* print current state *)
CASE state OF
| s0to0: Write.Line("0:0");
| s0to15: Write.Line("0:15");
| s0to30: Write.Line("0:30");
| s0to40: Write.Line("0:40");
| s15to0: Write.Line("15:0");
| s15to15: Write.Line("15:15");
| s15to30: Write.Line("15:30");
| s15to40: Write.Line("15:40");
| s30to0: Write.Line("30:0");
| s30to15: Write.Line("30:15");
| s30to30: Write.Line("30:30");
| s30to40: Write.Line("30:40");
| s40to0: Write.Line("40:0");
| s40to15: Write.Line("40:15");
| s40to30: Write.Line("40:30");
| deuce: Write.Line("Deuce");
| advantageA: Write.Line("Advantage A");
| advantageB: Write.Line("Advantage B");
| gameA: Write.Line("Game A"); EXIT
| gameB: Write.Line("Game B"); EXIT
END;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* store next valid input character into ch;
set ch to 0X (null-byte) if no valid input
is available
*)
LOOP (* until we get a valid input character
or no input is available *)
Read.Char(ch);
IF Streams.stdin.count = 0 THEN
ch := 0X;
EXIT
END;
IF (ch = "A") OR (ch = "B") THEN
EXIT
END;
IF (ch # " ") & (ch # ASCII.nl) THEN
Write.Line("Invalid input character found!");
ch := 0X;
EXIT
END;
END;
|
 | 0X ist das Nullbyte (also das Zeichen mit dem Wert 0).
|
 | Wir nutzen diesen Wert hier, um für den Rest des Programms
das Eingabe-Ende bzw. die Eingabe unzulässiger Zeichen
zu signalisieren.
|
 | Der OR-Operator liefert TRUE, falls einer
der beiden Operanden den Wert TRUE hat, andernfalls
FALSE.
|
 | Der &-Operator liefert TRUE, falls beide
Operanden den Wert TRUE haben, andernfalls FALSE.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* compute next state *) CASE ch OF | "A": CASE state OF | s0to0: state := s15to0; | s0to15: state := s15to15; | s0to30: state := s15to30; | s0to40: state := s15to40; | s15to0: state := s30to0; | s15to15: state := s30to15; | s15to30: state := s30to30; | s15to40: state := s30to40; | s30to0: state := s40to0; | s30to15: state := s40to15; | s30to30: state := s40to30; | s30to40: state := deuce; | s40to0: state := gameA; | s40to15: state := gameA; | s40to30: state := gameA; | deuce: state := advantageA; | advantageA: state := gameA; | advantageB: state := deuce; END; | "B": (* ... *) | 0X: (* no input available *) EXIT END; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Automaten in Oberon |
 | Datentyp CHAR |
 | Die CASE-Anweisung |
 | Die CASE-Anweisung II |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Einlese-Schleifen |
 | Einlese-Schleifen II |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Rahmen für den Tennis-Automaten |
 | Konstantendefinitionen |
 | Ausgabe des Zustands |
 | Einlese-Schleife |
 | Übergang zum Folgezustand |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sei L = L(G) eine formale Sprache, die durch die
Grammatik G definiert sei.
|
 | Sei A ⊆ L eine Menge von Sätzen,
die wir Axiome nennen. Alle Axiome werden als wahr
betrachtet, ohne daß dies zu beweisen ist.
|
 | Deduktionsregeln erlauben die Ableitung neuer
Theoreme aus den Axiomen und bereits bewiesener Theoreme.
|
 | Die Kombination aus einer formalen Sprache L mit
formellen Deduktionsregeln wird als formale Logik
bezeichnet.
|
 | Mit L kann eine Semantik assoziiert sein, die uns
angibt, welche Teilmenge T ⊆ L als wahr zu betrachten
ist. Wenn die Menge aller Sätze, die sich aus den Axiomen
under Verwendung der Deduktionsregeln ableiten lassen, zu
T gehören, dann ist die formale Logik wohlformuliert.
Wenn alle Elemente aus T abgeleitet werden können, ist sie
vollständig.
|
 | Literatur: Uwe Schöning, ``Logik für Informatiker''
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgende Grammatik G sei gegeben:
 | VT = { ⟨ Variable ⟩, ``¬'', ``=>'', ``('', ``)'' }
| |||||||||||||||
 | VN = { ⟨ Formula ⟩, ⟨ SimpleFormula ⟩ }
| |||||||||||||||
 | Produktionsregeln P:
| |||||||||||||||
 | Startsymbol: ⟨ Formula ⟩
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Eine Substitution S mit n Parametern ist eine Funktion
S : Ln -> L,
die spezifiziert wird durch
 | n Parameter p1, ···, pn und
|
 | einer Formel F ∈ L, in der p1, ···, pn
überall vorkommen dürfen, wo ⟨ Formula ⟩
zulässig ist.
|
Das Abbild von n Formeln P1, ···, Pn der Substitution S ist dann F, bei der textuell p1 durch P1 ersetzt wird, p2 durch P2, ··· und pn durch Pn.
Beispiel für eine Substitution mit einem Parameter:
S(p) := ¬ ¬ (p) => p
Anwendungsbeispiel: S(A => B) = ¬ ¬ (A => B) => A => B
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Bei der Aussagenlogik gibt es nur eine einzige Deduktionsregel, der sogenannte Modus Ponens:
Es seien zwei Theoreme oder Axiome folgender Form gegeben:
 | A
|
 | (A) => B
|
Hierbei sind A und B beliebige Formeln aus L.
Dann kann daraus B als neues Theorem abgeleitet werden.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Axiome sind alle Sätze aus L, die sich durch folgende Substitutionen erzeugen lassen:
 | H1(p1,p2) := (p1) => (p2) => p1
|
 | H2(p1,p2,p3) := ((p1) => (p2) => p3) => ((p1) => p2) => (p1) => p3
|
 | H3(p1,p2) := (¬ (p1) => ¬ (p2)) => (p2) => p1
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Läßt sich (A) => A (für beliebiges A ∈ L) ableiten? Ja:
| P1 | = | H1(A, (A) => A) |
| = | (A) => ((A) => A) => A | |
| P2 | = | H2(A, (A) => A, A) |
| = | ((A) => ((A) => A) => A) => ((A) => (A) => A) => (A) => A | |
| P3 | = | Modus Ponens(P1, P2) |
| = | ((A) => (A) => A) => (A) => A | |
| P4 | = | H1(A, A) |
| = | (A) => (A) => A | |
| P5 | = | Modus Ponens(P4, P3) |
| = | (A) => A |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Die Semantik kann als Funktion A : L -> {TRUE, FALSE} betrachtet werden, die jeder Formel F einen Wahrheitswert TRUE oder FALSE zuweist.
Sie wird praktischerweise rekursiv entlang der Produktionsregeln von G definiert:
 | Sei V die Menge aller Instantiierungen von
⟨ Variable ⟩ von G.
|
 | Sei A' : V -> {TRUE, FALSE} die Funktion, die jeder Variablen einen Wahrheitswert zuweist.
(Diese Funktion wird Belegung genannt).
|
 | ∀ v ∈ V: A(v) = A'(v)
|
 | A(¬ (F)) = { TRUE, & falls A(F) = FALSE FALSE, & falls A(F) = TRUE . |
 | A((F1) => F2) = { TRUE, & falls A(F1) = FALSE A(F2), & falls A(F1) = TRUE . |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Gegeben sei eine Formel F mit n Variablen. Da jeder der Variablen nur einen der Werte TRUE oder FALSE annehmen kann, können die 2n verschiedenen Wertekombinationen der Variablen von F zusammen mit A(F) in einer Tabelle zusammengefaßt werden.
Beispiele:
| A(F) | A(¬ (F)) |
| TRUE | FALSE |
| FALSE | TRUE |
| A(F1) | A(F2) | A((F1) => F2) |
| TRUE | TRUE | TRUE |
| TRUE | FALSE | FALSE |
| FALSE | TRUE | TRUE |
| FALSE | FALSE | TRUE |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Zwei Formeln F1 und F2 mit jeweils n Variablen v1, ···, vn können als äquivalent betrachtet werden, falls A(F1) = A(F2) für alle 2n möglichen Belegungen der Variablen v1, ···, vn.
Beispiel: A((A) => B) = A(¬ (B) => ¬ (A))
Der Nachweis kann durch die Verwendung von Wahrheitstafeln
durchgeführt werden.
Alle Formeln mit n Variablen können entsprechend dieser Äquivalenzrelation in Äquivalenzklassen einsortiert werden.
Wieviel Äquivalenzklassen kann es geben? Die Obergrenze ergibt sich durch die kombinatorische Vielfalt aller Wahrheitstabellen. Eine Wahrheitstabelle für n Variablen hat 2n Einträge und diese können alle jeweils mit TRUE oder FALSE belegt werden. Das ergibt dann 22n verschiedene Ausprägungen.
Wenn die Grundoperatoren geschickt ausgewählt werden (wie hier mit ¬ und =>), dann kann für jede denkbare Wahrheitstabelle auch eine Formel angegeben werden.
Bei n = 2 erhalten wir 22n = 24 = 16 verschiedene Wahrheitstabellen.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Hier sind alle 16 binären Boolean-Operatoren. Für die Übersicht wurde TRUE zu T und FALSE zu F abgekürzt. Es wird bei den Wahrheitstabellen jeweils einer der gebräuchlichen Namen oder Symbole für den Operator angegeben:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Es gelten die folgenden Äquivalenzen:
| A ∧ A | = A |
| A ∨ A | = A |
| A ∧ B | = B ∧ A |
| A ∨ B | = B ∨ A |
| (A ∧ B) ∧ C | = A ∧ (B ∧ C) |
| (A ∨ B) ∨ C | = A ∨ (B ∨ C) |
| A ∧ (A ∨ B) | = A |
| A ∨ (A ∧ B) | = A |
| A ∧ (B ∨ C) | = (A ∧ B) ∨ (A ∧ C) |
| A ∨ (B ∧ C) | = (A ∨ B) ∧ (A ∨ C) |
| ¬ (A ∧ B) | = ¬ A ∨ ¬ B |
| ¬ (A ∨ B) | = ¬ A ∧ ¬ B |
| A ∧ B | = ¬ (A => ¬ B) |
| A ∨ B | = ¬ A => B |
| A => B | = ¬ A ∨ B |
(partiell übernommen aus dem Werk von U. Schöning)
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Oberon bietet neben der Negation noch vier der binären Boolean-Operatoren an:
| Mathematische | Schreibweise in |
| Schreibweise | Oberon |
| ¬ A | ~A |
| A ∧ B | A & B |
| A ∨ B | A OR B |
| A <=> B | A = B |
| A xor B | A # B |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Während in der mathematischen Notation A und
B nur die Werte TRUE und FALSE annehmen können,
gibt es in Oberon auch noch die Möglichkeit, daß die Evaluation
einer der Operanden entweder undefiniert ist oder zu einem
Laufzeitfehler führt.
|
 | Beispiel: Was passiert bei der Bewertung von (j > 0) & (i MOD j = 0) falls j = 0? Hier würde die Bewertung des rechten Operanden des &-Operators zu einem Laufzeitfehler führen. |
 | Oberon (und viele andere Programmiersprachen) lassen dies
zu. Sie bewerten bei & und OR zunächst den linken
Operanden und betrachten den rechten Operanden dann und nur
dann, wenn das Resultat tatsächlich davon abhängt.
Das wird als Kurzschlußbewertung bezeichnet.
|
 | Interpretation von A & B: IF A THEN result := B; (* B wird bewertet *) ELSE result := FALSE; (* B bleibt unbewertet *) END; |
 | Interpretation von A OR B: IF A THEN result := TRUE; (* B bleibt unbewertet *) ELSE result := B; (* B wird bewertet *) END; |
 | Entsprechend verlieren diese Operatoren die
Eigenschaft der Kommutativität in Oberon.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Aus den Logeleien von Zweistein (dtv, 1984):
``Meiers werden uns heute abend besuchen'', kündigt Herr Müller an. ``Die ganze Familie, also Herr und Frau Meier nebst ihren drei Söhnen Tim, Kay und Uwe?'', fragte Frau Müller bestürzt. Darauf Herr Müller, der keine Gelegenheit vorübergehen läßt, seine Frau zum logischen Denken anzureizen: ``Nein, ich will es dir so erklären: Wenn Vater Meier kommt, dann bringt er auch seine Frau mit. Mindestens einer der beiden Söhne Uwe und Kay kommt. Entweder kommt Frau Meier oder Tim. Entweder kommen Tim und Kay oder beide nicht. Und wenn Uwe kommt, dann auch Kay und Herr Meier. So, jetzt weißt du, wer uns heute abend besuchen wird.''
Gegeben sind also 5 Variablen, die die Mitglieder der Familie Meier repräsentieren. In unserer Interpretation sind diese Variablen TRUE, falls die entsprechende Person kommt, ansonsten FALSE. Der informelle Text entspricht einer Formel der Aussagenlogik dieser fünf Variablen. Gesucht ist eine Belegung der fünf Variablen, so daß die Formel TRUE wird.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Variablen:
| ||||||||||
 | Erste Teilaussage:
``Wenn Vater Meier kommt, dann bringt er auch seine Frau mit.'' H => F | ||||||||||
 | Zweite Teilaussage:
``Mindestens einer der beiden Söhne Uwe und Kay kommt.'' U ∨ K | ||||||||||
 | Dritte Teilaussage:
``Entweder kommt Frau Meier oder Tim.'' F xor T | ||||||||||
 | Vierte Teilaussage:
``Entweder kommen Tim und Kay oder beide nicht.'' T <=> K | ||||||||||
 | Fünfte Teilaussage:
``Und wenn Uwe kommt, dann auch Kay und Herr Meier.'' U => (K ∧ H) | ||||||||||
 | Zusammengefaßt: (H => F) ∧ (U ∨ K) ∧ (F xor T) ∧ (T <=> K) ∧ (U => (K ∧ H)) |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
VAR herr, frau, tim, kay, uwe: BOOLEAN; a1, a2, a3, a4, a5: BOOLEAN; |
 | Die BOOLEAN-Variablen herr bis uwe
werden so interpretiert, daß bei einem Wert von TRUE
die betreffende Person zu Besuch kommt.
|
 | Aus Gründen der Übersichtlichkeit stehen die Variablen
a1 bis a5 für die Resultate der einzelnen Teilaussagen.
|
 | Für eine gegebene Belegung der Variablen herr bis uwe
liefert folgender Programmtext die Erkenntnis, ob die Belegung
die Gesamtbedingung erfüllt:
|
a1 := ~herr OR frau;
a2 := uwe OR kay;
a3 := frau # tim;
a4 := tim = kay;
a5 := ~uwe OR kay & herr;
IF a1 & a2 & a3 & a4 & a5 THEN
Write.Line("Loesung gefunden:");
IF herr THEN Write.Line("Herr Meier kommt") END;
IF frau THEN Write.Line("Frau Meier kommt") END;
IF tim THEN Write.Line("Tim kommt") END;
IF kay THEN Write.Line("Kay kommt") END;
IF uwe THEN Write.Line("Uwe kommt") END;
END;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Gegeben sei ein endlicher Raum für n-Tupel aus
R = R1 x ··· x Rn.
|
 | Problem: Wie erhalten wir alle möglichen Tupel aus R?
|
 | Lösung: Wir verwenden n ineinander verschachtelte
Schleifen. Die erste Schleife iteriert durch alle Werte
von R1, die zweite durch alle Werte von R2 usw.
|
 | Schematischer Aufbau in Pseudo-Code:
FOREACH i1 IN R1 DO |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | In Oberon gibt es keine FOREACH-Anweisung. Also
muß eine der anderen Schleifenkonstruktionen verwendet werden.
|
 | Im Falle eines ganzzahligen Intervalls [a..b]
geht dies beispielsweise mit einer WHILE-Schleife:
i := a; |
 | Ähnlich läßt sich das auch beim Datentyp CHAR
erledigen.
|
 | Für den seltenen Fall, daß die Obergrenze b auch
zugleich die Obergrenze des Datentyps ist, muß eine andere
Konstruktion verwendet werden:
i := a;
Hier gilt aber die Annahme, daß a <= b!
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Beim Datentyp BOOLEAN empfiehlt sich die
Verwendung einer REPEAT-Schleife:
i := FALSE; |
herr := FALSE; REPEAT frau := FALSE; REPEAT tim := FALSE; REPEAT kay := FALSE; REPEAT uwe := FALSE; REPEAT (* Untersuchung der Belegung *) uwe := ~uwe; UNTIL ~uwe; kay := ~kay; UNTIL ~kay; tim := ~tim; UNTIL ~tim; frau := ~frau; UNTIL ~frau; herr := ~herr; UNTIL ~herr; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Logelei in Oberon |
 | Iteration bei BOOLEAN |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Jede Variable und jeder Wert hat einen Typ in Oberon. Der Typ legt fest, welche Operationen zulässig sind und welche Semantik sie haben. Es gibt sowohl vordefinierte Typen in Oberon und Typkonstruktoren, mit denen neue Typen erzeugt werden können. Im Überblick:
 | Basistypen: SHORTINT, INTEGER, LONGINT,
REAL, LONGREAL, CHAR, BYTE, BOOLEAN,
SET.
|
 | Arrays: Feste Anzahl von Elementen gleichen Typs, die
indiziert werden mit ganzen Zahlen ab 0.
|
 | Records: Kombination mehrerer Typen zu einem Verbund.
|
 | Prozedurtypen
|
 | Zeigertypen (werden erst in Allgemeine Informatik II
vorgestellt).
|
Wichtig: Die Typen stehen grundsätzlich bereits zur Übersetzzeit fest und hängen nicht vom Laufzeitverhalten ab. (Ausnahmen gibt es später in Oberon bei Typerweiterungen, die erst in Allgemeine Informatik II behandelt werden).
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die numerischen Datentypen sind in Oberon hierarchisch
angeordnet: SHORTINT ⊆ INTEGER ⊆ LONGINT ⊆ ··· ··· ⊆ REAL ⊆ LONGREAL | |||||||||||||||
 | Grundsätzlich sind Operationen mit Operanden unterschiedlicher
numerischer Datentypen möglich. In diesem Falle findet im Vorfeld
immer einer Konvertierung des kleineren Datentyps zum umfangreicheren
Datentyp statt. Das Resultat ist dann vom umfangreicheren Typ.
| |||||||||||||||
 | Wird der Operator ``/'' auf zwei ganzzahlige Operanden
angewendet, so werden beide Operanden zu REAL konvertiert
und das Resultat ist ebenfalls von diesem Typ.
| |||||||||||||||
 | Wichtig: Alle Typen stehen bereits zur Übersetzzeit fest.
Das bedeutet beispielsweise, daß auch dann bei ``/'' eine
Konvertierung zu REAL stattfindet, wenn das konkrete
Resultat zur Laufzeit ganzzahlig ist.
| |||||||||||||||
 | Repräsentierungen beim Ulmer Oberon-System:
| |||||||||||||||
 | Gleitkommazahlen werden entsprechend IEEE 754-1985
repräsentiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Standard für die Repräsentierung von Gleitkommazahlen
und der zugehörigen arithmetischen Operationen. Wird von
allen gängigen Prozessoren heute unterstützt.
| ||||||
 | Die Repräsentierung besteht aus der Mantisse
(d0, d1, ···, dp-1) ∈ {0, 1}p,
dem Exponenten e ∈ [emin..emax] ⊆ |Z und
einem Vorzeichenbit s ∈ {-1, 1}. Interpretation:
| ||||||
 | Mehrere Repräsentierungen können für einen Wert möglich
sein. Beispiel:
d0 = 1, di = 0 ∀ i = 1..p-1, e = -1, s = 1 und auch als d0 = 0, d1 = 1, di =0 ∀ i = 2..p-1, e = 0, s = 1. | ||||||
 | Im Falle von d0 = 1 wird von einer normalisierten
Repräsentierung gesprochen.
| ||||||
 | Literatur: David Goldberg, ``What Every Computer
Scientist Should Know about Floating-Point Arithmetic'' http://www.validlab.com/goldberg/paper.ps |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE FPDemo;
IMPORT Write;
VAR
x: REAL; i: INTEGER;
BEGIN
x := 0; i := 0;
WHILE i < 10 DO
x := x + 0.1;
INC(i);
END;
IF x = 1.0 THEN
Write.Line("Exaktes Resultat!");
ELSE
Write.String("Ungenauigkeit: ");
Write.Real(x - 1.0, 1);
Write.Ln;
END;
END FPDemo.
|
 | Nicht nur irrationale Zahlen können nicht präzise
dargestellt werden, sondern auch viele rationale Zahlen. Beispiel: Für 0,1 (Dezimaldarstellung) gibt es keine exakte Darstellung. |
doolin$ FPDemo Ungenauigkeit: -1.110223D-0016 doolin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE FPRepr;
IMPORT Read, Reals, Streams, Write;
VAR
x: LONGREAL; (* input variable *)
exponent: INTEGER; (* exponent of x *)
mantissa: LONGREAL; (* mantissa of x *)
neg: BOOLEAN; (* negative? *)
ndigits: INTEGER; (* # of digits in digits *)
digits: ARRAY 64 OF CHAR; (* binary digits *)
BEGIN
LOOP
Write.String("x = "); Read.LongReal(x);
IF Streams.stdin.count = 0 THEN EXIT END;
Reals.ExpAndMan(x, (* long = *) TRUE,
(* base = *) 2,
exponent, mantissa);
Write.String("exponent = "); Write.Int(exponent, 1);
Write.Ln;
ndigits := 0; (* generate all significant digits *)
Reals.Digits(mantissa, (* base = *) 2, digits, neg,
(* force = *) FALSE, ndigits);
Write.String("mantissa = "); Write.Line(digits);
END;
END FPRepr.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
doolin$ FPRepr x = 1 exponent = 0 mantissa = 1 x = 2 exponent = 1 mantissa = 1 x = 57 exponent = 5 mantissa = 111001 x = 0.75 exponent = -1 mantissa = 11 x = 0.1 exponent = -4 mantissa = 1100110011001100110011001100110011001100110011001101 x = doolin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Ein Array ist ein Verbund von n Variablen des gleichen Typs
für ein beliebiges aber festes n ∈ |N.
| ||||||
 | Syntax:
| ||||||
 | Beispiele:
VAR vector: ARRAY 3 OF REAL; VAR matrix: ARRAY 3, 3 OF REAL; | ||||||
 | Die i-te Variable eines Arrays wird über einen
ganzzahligen Index angesprochen mit i ∈ [0..n-1].
Im Beispiel gibt es also vector[0], vector[1] und
vector[2]. Die Verwendung eines Indizes außerhalb
des zulässigen Bereiches führt zu einem Laufzeitfehler.
| ||||||
 | Bei den Indizes sind beliebige Ausdrücke zulässig,
deren Resultat von einem ganzzahligen Typ ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Folgender Algorithmus von R. A. Fisher und F. Yates
(1938) findet sich im Band 2 des Werks
``The Art of Computer Programming'' von D. Knuth:
| ||||||||
 | Algorithm P (Shuffling). Let
X1, X2, ···, Xt be a set of t numbers to be shuffled.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CONST maxlen = 32; VAR value: ARRAY maxlen OF INTEGER; (* to be shuffled *) len: INTEGER; (* value[0]..value[len-1] are in use *) j, k: INTEGER; (* indices of value *) randomval: REAL; (* pseudo-random out of [0..1) *) tmp: INTEGER; (* used during an exchange *) |
 | Da die Zahl der zu mischenden Zahlen nicht im voraus
bekannt ist, legen wir mit maxlen eine obere
Grenze fest und deklarieren entsprechend ein Array value
mit maxlen Variablen.
|
 | Zu beachten ist nur, daß im Algorithmus mit 1
beginnend indiziert wird, während in Oberon die Indizierung ab 0
erfolgt.
|
 | Beim Einlesen merken wir uns in len die Zahl
der eingelesenen Werte. Danach werden nur
value[0] bis value[len-1] betrachtet. Die Variable
len entspricht dem t aus dem Algorithmus.
|
 | Die Variablen j und k werden analog zum Algorithmus
verwendet.
|
 | Die Variable randomval entspricht dem U und
wird pseudo-zufällig bestimmt.
|
 | Für den Austausch im Schritt P3 wird die Hilfsvariable
tmp benötigt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
len := 0; LOOP Read.Int(value[len]); IF Streams.stdin.count = 0 THEN EXIT END; INC(len); IF len = maxlen THEN EXIT END; END; |
 | Der Inhalt der Variablen len entspricht genau
der Zahl der erfolgreich eingelesenen Werte.
|
 | Die Schleife wird beendet, sobald wir keine Zahl
einlesen konnten oder das Array vollständig gefüllt ist.
|
 | Auf eine Fehlermeldung für den Fall, daß das Array
zu klein ist, wurde verzichtet. In diesem Falle werden
die überzähligen Zahlen stillschweigend nicht eingelesen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF len > 1 THEN (* Algorithm P: Shuffling *) j := len; (* P1 *) REPEAT randomval := RandomGenerators.RealVal(); (* P2 *) k := SHORT(ENTIER(j * randomval)); (* P3 *) (* P4: exchange value[k] and value[j-1] *) tmp := value[k]; value[k] := value[j-1]; value[j-1] := tmp; DEC(j); (* P4 *) UNTIL j = 1; END; |
 | Das Modul RandomGenerators liefert gleichförmig
verteilte Pseudo-Zufallszahlen. RealVal liefert
hier einen gleichverteilten Wert aus [0..1).
|
 | ENTIER entspricht den abrundenden Gauß'schen
Klammern ⌊ ··· ⌋. Da ENTIER
den Datentyp LONGINT liefert, während k
vom Typ INTEGER ist, ist SHORT notwendig
für die Konvertierung von LONGINT zu INTEGER.
|
 | Bei P4 muß darauf geachtet werden, daß in Oberon
die Indizierung bei 0 beginnt. Entsprechend ist j-1
anstelle von j anzugeben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* print shuffled values *) j := 0; WHILE j < len DO Write.Int(value[j], 1); Write.Ln; INC(j); END; |
 | Am Ende sind die Werte value[0] bis value[len-1]
auszugeben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Problem: Für jeden in der Eingabe vorkommenden Buchstaben
ist die Häufigkeit anzugeben.
|
 | Groß- und Kleinbuchstaben sind dabei als äquivalent
zu betrachten.
|
 | Ideal wäre ein Array, das mit Buchstaben indiziert
werden kann. Da das in Oberon nicht umsetzbar ist, müssen
die Buchstaben ``A''..``Z'' in den Zahlenbereich 0..25
abgebildet werden.
|
 | Konstanten wie 25 oder 26, die überall im Programmtext
verstreut sind, erschweren die Lesbarkeit des Programms,
da dann häufig die Frage auftaucht, wofür die Zahl steht
und ob diese Konstante mit anderen Konstanten zusammenhängt.
|
 | Deswegen sollten Konstanten mit Hilfe von CONST einen
Namen erhalten und anschließend sollte nur noch der Name
verwendet werden.
|
CONST
letters = ORD("Z") - ORD("A") + 1;
VAR
count: ARRAY letters OF INTEGER;
i: INTEGER; (* index of count *)
ch: CHAR; (* input character *)
letter: BOOLEAN; (* is ch a letter? *)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* count letters *)
WHILE Streams.ReadByte(Streams.stdin, ch) DO
CASE ch OF
| "a".."z":
(* convert it to upper-case *)
ch := CAP(ch);
letter := TRUE;
| "A".."Z":
letter := TRUE;
ELSE
letter := FALSE;
END;
IF letter THEN
i := ORD(ch) - ORD("A");
INC(count[i]);
END;
END;
|
 | Streams.ReadByte liest ein Zeichen von dem
angegebenen Stream und liefert TRUE, falls die
Operation erfolgreich war. Die Verwendung von
Streams.ReadByte führt im Vergleich zu Read.Char
zu eleganteren Schleifen.
|
 | Mit CAP werden Kleinbuchstaben zu Großbuchstaben
konvertiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* print counts *)
i := 0;
WHILE i < letters DO
IF count[i] > 0 THEN
Write.Char(CHR(i + ORD("A")));
Write.String(": ");
Write.Int(count[i], 1);
Write.Ln;
END;
INC(i);
END;
|
 | Für die Ausgabe muß der Index i
jeweils in einen Buchstaben abgebildet werden.
Dies geschieht, indem zunächst zu i der
Ordinalwert von ``A'' addiert wird. Danach
konvertiert CHR den so gewonnen Ordinalwert
in ein Zeichen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Oberon bietet einen Basistyp für kleine Mengen an: SET.
| ||||||||||||||||||||
 | Mögliche Elemente einer Menge vom Typ SET sind die
ganzen Zahlen zwischen 0 und MAX(SET).
| ||||||||||||||||||||
 | Bei unserer Implementierung hat MAX(SET) den Wert 31.
| ||||||||||||||||||||
 | Größere Mengen werden über Arrays realisiert. Das wird
vom Modul Sets unterstützt.
| ||||||||||||||||||||
 | Beispiel: VAR set: SET;
| ||||||||||||||||||||
 | Mengen können mit geschweiften Klammern konstruiert werden. Beispiel: set := {3, 4, 7..10, i-1..j}; | ||||||||||||||||||||
 | Operatoren für Mengen:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Gegeben seien n Netzwerkknoten, die teilweise
miteinander (bidirektional) verbunden sind. Wenn die Knoten A
und B miteinander verbunden sind und Knoten B mit Knoten
C eine Verbindung unterhält, dann ist C auch von A
aus erreichbar (Transitivität).
|
 | Probleme: Welche Knoten sind von einem gegebenen Knoten
aus erreichbar? Wieviele unabhängige ``Inseln'' liegen
vor, die nicht miteinander verbunden sind, und wie sehen
diese aus?
|
 | Formal läßt sich das als Relation
N ⊆ [1..n] x [1..n] ⊆ |N2 betrachten, die
reflexiv, transitiv und symmetrisch ist.
|
 | Spezifiziert werden kann die Relation durch eine
Menge von direkt miteinander verbundenen Paaren (ai,bi),
wobei wegen der Reflexivität (ai,ai) und (bi,bi)
und wegen der Symmetrie (bi,ai) implizit angenommen werden.
|
 | Zusätzlich müssen die transitiven Hüllen berechnet werden,
d.h. falls (a,b) und (b,c) in der Relation enthalten sind,
muß auch (a,c) aufgenommen werden.
|
 | Beispiel: Gegeben seien die Paare
(1, 2), (3, 4), (5, 2), (6, 3), (7, 1), dann ist
die transitive Hülle von 1 gleich {1, 2, 5, 7}
und die von 3 gleich {3, 4, 6}.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CONST (* we support node numbers from 0 to maxnode *) maxnode = MAX(SET); nodes = maxnode + 1; VAR connected: ARRAY nodes OF SET; (* connected[i] = set of nodes i is connected to *) node: INTEGER; (* index of connected *) seen: SET; (* set of nodes seen in input *) node1, node2: INTEGER; (* pair of nodes *) closure: SET; (* transitive closure of a node *) printed: SET; (* set of printed nodes *) |
 | Wir nehmen hier an, daß n <= MAX(SET) + 1.
|
 | Entsprechend repräsentiert connected[i] die
Menge {j | (i,j) ∈ N }.
|
 | Um nur die Knoten zu berücksichtigen, die tatsächlich
in der Eingabe erwähnt wurden, wird in der Menge seen
die Menge aller eingelesenen Knotennummern notiert.
|
 | node1 und node2 repräsentieren jeweils
ein Knotenpaar.
|
 | closure wird bei der Berechnung der transitiven
Hülle benötigt.
|
 | Bei der Ausgabe soll jeder Knoten nur einmal ausgegeben
werden. Das wird mit Hilfe der Menge printed
sichergestellt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* initializations *)
node := 0;
WHILE node < nodes DO
connected[node] := {};
INC(node);
END;
seen := {};
|
 | Vor dem Einlesen muß die Datenstruktur initialisiert
werden.
|
 | repräsentiert die leere Menge.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* read pairs of connected nodes *)
LOOP
Read.Int(node1);
IF Streams.stdin.count = 0 THEN EXIT END;
IF (node1 < 0) OR (node1 > maxnode) THEN
Write.Line("Invalid node number!");
EXIT
END;
Read.Int(node2);
IF Streams.stdin.count = 0 THEN
Write.Line("Odd number of integers in input!");
EXIT
END;
IF (node2 < 0) OR (node2 > maxnode) THEN
Write.Line("Invalid node number!");
EXIT
END;
(* connections are bidirectional *)
INCL(connected[node1], node2);
INCL(connected[node2], node1);
INCL(seen, node1); INCL(seen, node2);
END;
|
 | Beim Eintragen in die Datenstruktur wird zunächst
nur die Symmetrie berücksichtigt. Die transitiven Hüllen
werden erst nach dem Einlesen aller Paare berechnet. Die
Reflexivität ergibt sich dann implizit aus der Symmetrie,
der Transitivität und der Tatsache, daß jeder vorkommende
Knoten mindestens mit einem anderen Knoten in Verbindung
steht. (Ein isolierter Knoten kann dann immer noch als
Paar mit sich selbst spezifiziert werden).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Gegeben sei die Relation R und a ∈ R. Dann läßt sich die transitive Hülle folgendermaßen bestimmen:
 | Setze C <- {a}.
|
 | Setze C' <- C.
|
 | Bestimme für jedes c ∈ C die Menge
T = {t | (c,t) ∈ R}.
|
 | Setze C <- C ∪ T.
|
 | Springe zu T2, falls C ≠ C'.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* compute transitive closures *)
node1 := 0;
WHILE node1 < nodes DO
IF connected[node1] # {} THEN
closure := connected[node1];
LOOP
node2 := 0;
WHILE node2 < nodes DO
IF node2 IN closure THEN
closure := closure + connected[node2];
END;
INC(node2);
END;
IF closure = connected[node1] THEN
EXIT
END;
connected[node1] := closure;
END;
END;
INC(node1);
END;
|
 | Zu beachten ist, daß T3 zwei ineinander geschachtelte
Schleifen benötigt. Die äußere Schleife durchläuft
alle c ∈ C (in Oberon alle node2 IN closure) und
die innere berechnet jeweils T = {t | (c,t) ∈ R}.
|
 | In Oberon werden die Resultate von T3 sogleich entsprechend
dem Schritt T4 in C aufgesammelt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* print connected networks *)
printed := {};
node1 := 0;
WHILE node1 < nodes DO
IF (node1 IN seen) & ~(node1 IN printed) THEN
node2 := 0;
WHILE node2 < nodes DO
IF node2 IN connected[node1] THEN
Write.Int(node2, 3);
INCL(printed, node2);
END;
INC(node2);
END;
Write.Ln;
END;
INC(node1);
END;
|
 | Um die mehrfache Ausgabe der gleichen transitiven Hülle
(für alle darin enthaltenen Knoten) zu vermeiden, wird
mittels der Menge printed notiert, welche Knoten bereits
ausgegeben worden sind.
|
 | Ein Schleifendurchlauf wird (im Normalfall) gespart,
indem wir sogleich von connected[node1] ausgehen und
nicht nur von {node1}.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seite im Skript |
 | Gleitkommazahlen nach IEEE 754-1985 II |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seite im Skript |
 | Gleitkommazahlen nach IEEE 754-1985 III |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Datenstrukturen für das Mischen |
 | Einlesen der zu mischenden Werte |
 | Der Misch-Algorithmus |
 | Ausgabe des Arrays |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Zählen von Buchstaben |
 | Zählen von Buchstaben II |
 | Zählen von Buchstaben III |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Datenstruktur für die Relation |
 | Datenstruktur für die Relation II |
 | Einlesen der Knotenpaare |
 | Berechnen der transitiven Hülle II |
 | Ausgabe der transitiven Hüllen |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Ein Record ist ein Verbund mehrerer Variablen (Felder
genannt), die unterschiedlichen Typs sein können.
| |||||||||||||||
 | Die einzelnen Felder eines Records erhalten dabei Namen.
| |||||||||||||||
 | Syntax:
| |||||||||||||||
 | Beispiele: TYPE Name = ARRAY 80 OF CHAR; TYPE Datum = RECORD tag, monat: SHORTINT; jahr: INTEGER END; TYPE Person = RECORD name: Name; gebdatum: Datum END; VAR person1, person2: Person; | |||||||||||||||
 | person1 bezeichnet dann eine vollständige Person und bei person1 := person2; werden alle Felder von person2 zu person1 kopiert. | |||||||||||||||
 | Einzelne Felder lassen sich mit dem Punkt selektieren,
so steht person1.name für den Namen von person1 und
person1.gebdatum.monat für den Geburtsmonat von person1.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Zu implementieren ist ein kleines Adreßbuch fester
Größe mit 16 Einträgen, in die jeweils Namen und Ortschaften
eingetragen werden können.
|
 | Adressen sollen interaktiv eingegeben, aufgelistet und
gelöscht werden können.
|
 | So könnte die Datenstruktur dafür aussehen:
|
CONST maxentries = 16; (* maximal number of entries in an address book *) TYPE Name = ARRAY 80 OF CHAR; Entry = RECORD used: BOOLEAN; (* is this entry in use? *) name: Name; city: Name; END; AddressBook = ARRAY maxentries OF Entry; VAR addressBook: AddressBook; index: INTEGER; (* of addressBook *) command: ARRAY 16 OF CHAR; (* command read from input *) entry: Entry; (* a new entry; used by ``new'' *) name: Name; (* used as arg for ``search'' or ``delete'' *) |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* initialize address book: mark all entries as unused *) index := 0; WHILE index < maxentries DO addressBook[index].used := FALSE; INC(index); END; |
 | Zu Beginn werden alle Einträge des Adreßbuches als
ungenutzt markiert, d.h. das Feld used ist jeweils
auf FALSE zu setzen.
|
 | Die übrigen Felder bleiben undefiniert.
|
 | Danach sieht das Adreßbuch etwa folgendermaßen aus:
|

![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Für Zeichenketten werden in diesem Beispiel
festdimensionierte Arrays mit CHAR als Elementtyp
verwendet.
|
 | Da die Zeichenketten normalerweise etwas kürzer sind,
wird jeweils ein Nullbyte (0X) als Endzeichen
verwendet.
|
 | Folgendes Beispiel zeigt ein ARRAY 12 OF CHAR,
das mit der Zeichenkette ``Hallo!'' gefüllt wurde:
|

 | Die Operatoren = und # sind für beliebige
Zeichenketten in Oberon zulässig.
|
 | Die Zuweisung klappt nur, wenn beide Seiten den
identischen Typ haben. In den anderen Fällen empfiehlt
sich die Verwendung von COPY. Beispiel: VAR a: ARRAY 12 OF CHAR; VAR b: ARRAY 32 OF CHAR; (* ... *) COPY(b, a); (* a := b *) Wenn die Zeichenkette von b länger ist als der Platz in a, dann wird entsprechend abgeschnitten. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
LOOP
Write.String("address book> ");
Read.Line(command);
IF Streams.stdin.count = 0 THEN EXIT END;
IF command = "quit" THEN EXIT END;
IF command = "new" THEN
(* fill new entry *)
ELSIF command = "list" THEN
(* list all entries *)
ELSIF command = "search" THEN
(* search for an entry by a name *)
ELSIF command = "delete" THEN
(* delete an entry with the given name *)
ELSIF command = "help" THEN
(* print help information *)
ELSE
Write.Line("Unknown command. Please try ``help''!");
END;
END;
|
 | Read.Line liest eine vollständige Zeile ein
und legt den Zeileninhalt (soweit es geht) ohne den
Zeilentrenner in dem übergebenen Array ab.
|
 | Die CASE-Anweisung ist nicht für Zeichenketten
zulässig. Entsprechend muß ersatzweise eine ELSIF-Kette
verwendet werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* fill new entry *)
entry.used := TRUE;
Write.String("Name: "); Read.Line(entry.name);
Write.String("City: "); Read.Line(entry.city);
(* look for a free slot *)
index := 0;
WHILE (index < maxentries) & addressBook[index].used DO
INC(index);
END;
IF index = maxentries THEN
Write.Line("Sorry, your address book is already full!");
ELSE
addressBook[index] := entry;
END;
|
 | Zunächst werden in entry alle Angaben eingetragen.
|
 | Danach wird nach einem freien Eintrag im Adreßbuch gesucht.
|
 | Records des identischen Typs können einander zugewiesen
werden. Dann werden sämtliche Felder kopiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* list all entries *)
index := 0;
WHILE index < maxentries DO
IF addressBook[index].used THEN
Write.String(addressBook[index].name);
Write.String(", ");
Write.Line(addressBook[index].city);
END;
INC(index);
END;
|
 | Bei der Ausgabe dürfen wir nur die tatsächlich
genutzten Einträge berücksichtigen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* search for an entry by a name *)
Write.String("Name: "); Read.Line(name);
index := 0;
WHILE (index < maxentries) &
(~addressBook[index].used OR
(addressBook[index].name # name)) DO
INC(index);
END;
IF index = maxentries THEN
Write.Line("Sorry, not found!");
ELSE
Write.String(addressBook[index].name);
Write.String(", ");
Write.Line(addressBook[index].city);
END;
|
 | Die WHILE-Schleife darf erst beendet werden,
wenn wir das Adreßbuch vollständig durchgeschaut
haben oder wir einen Eintrag mit dem gewünschten
Namen gefunden haben. Bei letzterem dürfen natürlich
nur genutzte Einträge betrachtet werden.
|
 | Alternativ könnte die WHILE-Bedingung nach
der Anwendung der de Morgan'schen Regel auch so formuliert
werden:
WHILE (index < maxentries) &
Welche Variante nun bevorzugt wird, ist Geschmackssache.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* delete an entry with the given name *)
Write.String("Name: "); Read.Line(name);
index := 0;
WHILE (index < maxentries) &
(~addressBook[index].used OR
(addressBook[index].name # name)) DO
INC(index);
END;
IF index = maxentries THEN
Write.Line("Sorry, not found!");
ELSE
addressBook[index].used := FALSE;
END;
|
 | Das Löschen ist sehr ähnlich zum Suchen. Nur wird
der Eintrag nicht ausgegeben, sondern das used-Feld
wird nur auf FALSE gesetzt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
index := 0; WHILE (index < maxentries) & (~addressBook[index].used OR (addressBook[index].name # name)) DO INC(index); END; |
 | Dieser Programmtext kommt im letzten Beispiel zweifach
vor: Zum einen bei der Bearbeitung des Suche-Befehls und
zum anderen beim Löschen.
|
 | Bei größeren Programmen ist das sehr ungeschickt,
da dann notwendige Änderungen (Fehlerbehebungen oder
Anpassungen der Datenstruktur) an unnötig vielen Stellen
durchgeführt werden müssen.
|
 | Deswegen ist es sinnvoll, mehrfach benötigten Programmtext
separat aufzuschreiben, ihn zu benennen und an verschiedenen
Stellen über den Namen aufzurufen. Der herausgetrennte
Programmtext nennt sich dann eine Prozedur.
|
 | Prozeduren sind auch dann sinnvoll, wenn sie nur an einer
Stelle aufgerufen werden, da sie sehr zur Übersicht eines
Programmes beitragen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE SearchByName(addressBook: AddressBook; name: Name; VAR index: INTEGER) : BOOLEAN; (* search for the first entry with the given name in the address book; set index to its array index and return TRUE, if successful; return FALSE otherwise *) BEGIN index := 0; WHILE (index < maxentries) & (~addressBook[index].used OR (addressBook[index].name # name)) DO INC(index); END; RETURN index < maxentries END SearchByName; |
 | Prozeduren bestehen aus einem Namen (hier SearchByName),
dann einer Reihe von formalen Parametern
(hier addressBook, name und index), einem
optionalen Typ bei Funktionen, lokalen Deklarationen (fehlen hier)
und Programmtext.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE SearchByName(addressBook: AddressBook; name: Name; VAR index: INTEGER) : BOOLEAN; |
 | Die formale Parameterliste sieht ähnlich aus
wie Variablendeklarationen. Allerdings hat VAR hier
eine völlig andere Bedeutung.
| |||||||||||||||||||||||||||||||||||||||||||||
 | Vollständige Syntax für Prozeduren:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF ReadName(name) THEN
IF SearchByName(addressBook, name, index) THEN
PrintEntry(addressBook[index]);
ELSE
Write.Line("Sorry, not found!");
END;
END;
|
 | Ein Prozedur-Aufruf besteht aus dem Namen einer
Prozedur und den aktuellen Parametern.
|
 | Der Aufruf beginnt zunächst mit der Parameterübergabe
(bzw. deren Zuordnung). Danach übernimmt der Programmtext
der Prozedur die Kontrolle. Sobald die Prozedur beendet ist,
wird die Ausführung beim Aufrufer fortgesetzt. Wird (wie
hier bei SearchByName ein Wert zurückgegeben
(vom Typ BOOLEAN) so wird dieser Rückgabewert genau
an der Stelle eingesetzt, wo der Aufruf steht.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE SearchByName(addressBook: AddressBook; name: Name; VAR index: INTEGER) : BOOLEAN; |
 | Oberon unterstützt zwei Arten von Parametern:
Werte-Parameter (call by value) und
Referenz-Parameter (call by reference).
|
 | Referenz-Parameter werden in der formalen Parameterliste
mit dem Schlüsselwort VAR markiert (und daher
auch als VAR-Parameter bezeichnet).
Alle anderen Parameter sind Werte-Parameter.
|
 | Werte-Parameter sind Variablen, die der Prozedur alleine
gehören. Sie werden zu Beginn des Prozeduraufrufs neu
erzeugt und verschwinden am Ende des Prozeduraufrufs.
|
 | Werte-Parameter werden mit den Werten der
entsprechenden aktuellen Parameter initialisiert. D.h.
die Werte werden kopiert und danach gibt es keinen
Zusammenhang mehr zwischen den aktuellen und formellen
Parametern.
|
 | Referenz-Parameter sind Alias-Namen für die entsprechenden
aktuellen Parameter. Wenn innerhalb der Prozedur der
Referenz-Parameter verändert oder ausgewertet wird bezieht
sich das immer auf die Variable aus der aktuellen Parameterliste.
|
 | Bei SearchByName sind addressBook und
name Werte-Parameter, während es sich bei index
um einen Referenz-Parameter handelt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo1;
IMPORT Write;
VAR i: INTEGER;
PROCEDURE P(val: INTEGER);
BEGIN
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
INC(val);
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
Write.String("P: i = "); Write.Int(i, 1); Write.Ln;
END P;
BEGIN
i := 1; P(i);
Write.String("Main: i = "); Write.Int(i, 1); Write.Ln;
END ParamDemo1.
|
 | Beim Aufruf von P wird der Wert des aktuellen
Parameters (hier: 1) zum formellen Parameter val
kopiert.
|
 | Wenn val später innerhalb der Prozedur verändert
wird, betrifft dies nicht die Variable i.
|
dublin$ ParamDemo1 P: val = 1 P: val = 2 P: i = 1 Main: i = 1 dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo2;
IMPORT Write;
VAR i: INTEGER;
PROCEDURE P(VAR val: INTEGER);
BEGIN
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
INC(val);
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
Write.String("P: i = "); Write.Int(i, 1); Write.Ln;
END P;
BEGIN
i := 1; P(i);
Write.String("Main: i = "); Write.Int(i, 1); Write.Ln;
END ParamDemo2.
|
 | Hier wird beim Aufruf von P kein Wert kopiert,
sondern val wird während des Aufrufs zu einem
neuen Namen der Variablen i.
|
dublin$ ParamDemo2 P: val = 1 P: val = 2 P: i = 2 Main: i = 2 dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo3;
IMPORT Write;
VAR i: INTEGER;
PROCEDURE P(VAR val: INTEGER);
BEGIN
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
INC(i);
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
Write.String("P: i = "); Write.Int(i, 1); Write.Ln;
END P;
BEGIN
i := 1; P(i);
Write.String("Main: i = "); Write.Int(i, 1); Write.Ln;
END ParamDemo3.
|
 | val und i sind in diesem Beispiel Synonyme.
Also macht es keinen Unterschied, ob hier INC(val) oder
INC(i) steht.
|
dublin$ ParamDemo3 P: val = 1 P: val = 2 P: i = 2 Main: i = 2 dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo4;
IMPORT Write;
PROCEDURE P(val: INTEGER);
BEGIN
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
INC(val);
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
END P;
BEGIN
P(3 - 2);
END ParamDemo4.
|
 | Bei Werte-Parametern können beim entsprechenden
aktuellen Parameter beliebige Ausdrücke stehen.
|
 | Voraussetzung ist nur, daß der Typ des Ausdrucks an
den Typ des formellen Parameters zugewiesen werden kann.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo5;
IMPORT Write;
PROCEDURE P(VAR val: INTEGER);
BEGIN
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
INC(val);
Write.String("P: val = "); Write.Int(val, 1); Write.Ln;
END P;
BEGIN
P(3 - 2);
END ParamDemo5.
|
 | Bei Referenz-Parametern muß eine veränderbare Größe
übergeben werden (designator).
|
dublin$ make oc -c -u ParamDemo5.om 12 P(3 - 2); ^ designator expected for VAR-parameter make: *** [ParamDemo5.o] Error 1 dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ParamDemo6; IMPORT Write; VAR i: LONGINT; PROCEDURE P(VAR val: INTEGER); BEGIN END P; BEGIN i := 1; P(i); END ParamDemo6. |
 | Der Typ des aktuellen Parameters muß identisch sein
zum Typ des aktuellen Parameters.
|
dublin$ make ParamDemo6 oc -c -u ParamDemo6.od ParamDemo6.om 11 i := 1; P(i); ^ type identity to "INTEGER" required make: *** [ParamDemo6.sy] Error 1 dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Der Parameterübergabe-Mechanismus dient der Kommunikation
zwischen dem Aufrufer und der Prozedur.
|
 | Werte-Parameter dienen der unidirektionalen Kommunikation
vom Aufrufer zur Prozedur. Beispiel: Write.Int |
 | Referenz-Parameter können verwendet werden, um von der
Prozedur berechnete oder bestimmte Werte an Variablen
des Aufrufers zuzuweisen. In diesem Falle spielt der Wert
der Variablen vor dem Aufruf keine Rolle. Beispiel: Read.Int |
 | Referenz-Parameter können aber auch für eine bidirektionale
Kommunikation verwendet werden. Dann betrachtet die Prozedur
den Wert der auf diese Weise übergebenen Variable und hat
dann die Möglichkeit, den Wert der Variable zu verändern.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE SearchByName(addressBook: AddressBook; name: Name; VAR index: INTEGER) : BOOLEAN; |
 | Neben den ``normalen'' Prozeduren gibt es auch
die sogenannten Funktionsprozeduren, die einen Rückgabewert
so liefern, daß er direkt in einen Ausdruck eingebaut werden kann.
|
 | Als Rückgabetyp sind keine Record- oder Array-Typen
zugelassen. Wenn dafür Bedarf besteht, sind stattdessen
entsprechende Referenz-Parameter zu verwenden.
|
 | Wenn eine Funktions-Prozedur aufgerufen wird, muß auch
der Rückgabewert in einen Ausdruck eingebaut werden. Dies
ist auch dann notwendig, wenn dieser aus der Sicht des
Aufrufers völlig uninteressant ist.
|
 | Sehr beliebt ist BOOLEAN als Typ für einen Rückgabewert,
um Erfolg oder Mißerfolg des Prozeduraufrufs zu signalisieren.
Im Beispiel von SearchByName liefert die Prozedur TRUE
zurück, falls der Name gefunden wurde und ansonsten FALSE.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE InitAddressBook(VAR addressBook: AddressBook); (* initialize address book: mark all entries as unused *) VAR index: INTEGER; BEGIN index := 0; WHILE index < maxentries DO addressBook[index].used := FALSE; INC(index); END; END InitAddressBook; |
 | Bei jeder Prozedur sind beliebige Deklarationen zulässig,
die dann nur innerhalb der Prozedur sichtbar sind.
|
 | Dazu gehören auch insbesondere Variablen, die als
lokale Variablen bezeichnet werden, weil sie nur
innerhalb der Prozedur lokal sichtbar sind. Variablen eines
Moduls werden globale Variablen genannt, da sie für
alle Prozeduren des Moduls sichtbar sind.
|
 | Lokale Variablen werden erzeugt, sobald eine Prozedur
aufgerufen wird und sie verschwinden automatisch wieder,
sobald die Prozedur beendet ist. In dieser Hinsicht sind
sie ähnlich wie die Werte-Parameter, nur daß sie eben
nicht von Anfang an durch die Parameterübergabe initialisiert sind.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Globale Variablen sind soweit wie möglich zu vermeiden.
| ||||||
 | Je weniger globale Variablen verwendet werden, umso weniger
stellt sich die Frage, wer auf diese auf welche Weise zugreift.
| ||||||
 | Globale Variablen sind nur sinnvoll in folgenden Fällen:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE ReadName(VAR name: Name) : BOOLEAN;
(* read a name and return TRUE if successful;
note that we return FALSE
in case of empty input lines
*)
BEGIN
Write.String("Name: "); Read.Line(name);
RETURN (Streams.stdin.count > 0) & (name # "")
END ReadName;
|
 | Einlese-Operationen lassen sich gut in Prozeduren
einbetten.
|
 | Wenn diese Prozeduren ein BOOLEAN-Resultat
je nach Erfolg liefern, dann lassen sich die weniger
eleganten LOOP-Einleseschleifen in elegante
WHILE-Schleifen konvertieren.
|
PROCEDURE ReadCity(VAR city: Name) : BOOLEAN;
(* read a name and return TRUE if successful;
note that we permit an empty input line
*)
BEGIN
Write.String("City: "); Read.Line(city);
RETURN Streams.stdin.count > 0
END ReadCity;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE ReadEntry(VAR entry: Entry) : BOOLEAN; (* read a new entry; return TRUE if successful *) BEGIN entry.used := TRUE; RETURN ReadName(entry.name) & ReadCity(entry.city) END ReadEntry; |
 | Wenn konsequent die Einlese-Operationen als
BOOLEAN-wertige Funktions-Prozeduren zur Verfügung
stehen, dann können diese gut kombiniert werden.
|
 | Wegen der Kurzschluß-Bewertung wird die &-Kette
sofort abgebrochen, sobald eine der Funktions-Prozeduren
FALSE liefert. Somit ist bei Eingabe-Ende auch
wirklich gleich Schluß.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE FindFreeSlot(addressBook: AddressBook; VAR index: INTEGER) : BOOLEAN; (* look for an unused slot within the address book; set index and return TRUE, if successful; return FALSE if there are no free slots left *) BEGIN index := 0; WHILE (index < maxentries) & addressBook[index].used DO INC(index); END; RETURN index < maxentries END FindFreeSlot; |
 | Einzelne Operationen wie beispielsweise das
Finden eines freien Feldes im Array lassen sich
elegant in einzelne Prozeduren packen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE PrintEntry(entry: Entry);
(* print an entry that is in use *)
BEGIN
ASSERT(entry.used);
Write.String(entry.name);
IF entry.city # "" THEN
Write.String(", ");
Write.Line(entry.city);
END;
END PrintEntry;
PROCEDURE PrintEntries(addressBook: AddressBook);
(* print all used entries of the given address book *)
VAR
index: INTEGER;
BEGIN
index := 0;
WHILE index < maxentries DO
IF addressBook[index].used THEN
PrintEntry(addressBook[index]);
END;
INC(index);
END;
END PrintEntries;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE ProcessCommands;
(* maintain an address book
by processing commands for it
*)
VAR
addressBook: AddressBook;
index: INTEGER; (* of addressBook *)
command: ARRAY 16 OF CHAR;
(* command read from input *)
entry: Entry; (* a new entry; used by ``new'' *)
name: Name;
(* used as arg for ``search'' or ``delete'' *)
BEGIN
InitAddressBook(addressBook);
LOOP
Write.String("address book> ");
Read.Line(command);
IF Streams.stdin.count = 0 THEN EXIT END;
(* ... process command ... *)
END;
END ProcessCommands;
|
 | Durch die Abwesenheit globaler Variablen findet
kein unbeabsichtiger Zugriff auf die Variablen statt,
die für die Verwaltung notwendig sind.
|
 | Stattdessen werden die Zugriffe durch die
Prozeduraufrufe reglementiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF command = "quit" THEN EXIT END;
IF command = "new" THEN
IF FindFreeSlot(addressBook, index) THEN
IF ReadEntry(entry) THEN
addressBook[index] := entry;
END;
ELSE
Write.Line("Sorry, your address book is already full!");
END;
ELSIF command = "list" THEN
PrintEntries(addressBook);
ELSIF command = "search" THEN
IF ReadName(name) THEN
IF SearchByName(addressBook, name, index) THEN
PrintEntry(addressBook[index]);
ELSE
Write.Line("Sorry, not found!");
END;
END;
ELSIF command = "delete" THEN
IF ReadName(name) THEN
IF SearchByName(addressBook, name, index) THEN
addressBook[index].used := FALSE;
ELSE
Write.Line("Sorry, not found!");
END;
END;
ELSIF command = "help" THEN
Write.String("Supported commands: ");
Write.Line("delete, help, list, new, quit, search");
ELSE
Write.Line("Unknown command. Please try ``help''!");
END;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Werte-Parameter |
 | Referenz-Parameter |
 | Referenz-Parameter II |
 | Werte-Parameter |
 | Referenz-Parameter |
 | Referenz-Parameter II |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Prozesse können viele Ein- und Ausgabe-Verbindungen
unterhalten.
|
 | Einige davon stehen gleich zu Beginn zur Verfügung wie
beispielsweise Streams.stdin, Streams.stdout
und Streams.stderr.
|
 | Zusätzlich können weitere Verbindungen eröffnet
und wieder geschlossen werden.
|
 | Ein- und Ausgabe-Verbindungen sind abstrakt, d.h.
sie können zu sehr unterschiedliche Arten von Medien
verbunden sein, z.B. zu dem xterm, in dem der Prozess
gestartet wurde, zu einer Datei, zu einem anderen Prozess
über eine Pipeline oder gar zu einem Prozess auf einem
anderen Rechner über eine Netzwerkverbindung.
|
 | Verbindungen zu diversen Geräten wie Drucker oder
Bandlaufgeräte sind ebenfalls möglich.
|
 | Ferner kann es in Oberon auch interne Ein- und
Ausgabe-Verbindungen geben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Eine Datei entspricht im idealen Falle einem Array aus Bytes.
|
 | Wenn eine Datei eine Länge von n Bytes hat, sind diese
über die Positionen 0 bis n-1 abrufbar.
|
 | Eine Dateiverbindung hat eine aktuelle Position p.
|
 | Wenn ein Byte über eine Verbindung gelesen oder geschrieben
wird, dann erfolgt der Zugriff auf der aktuellen Position p,
die anschließend, falls die Operation erfolgreich war, um
eins erhöht wird.
|
 | Lese-Operationen bei einer Position von n sind nicht
erfolgreich.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Ein unidirektionaler Kommunikationskanal verbindet
einen Produzenten, der in den Kanal schreibt, mit einem
Konsumenten, der aus dem Kanal liest.
|
 | Beispiel: Pipeline unter UNIX
|
 | Die Speicherkapazität des Kanals ist beschränkt,
d.h. der Produzent kann nicht beliebig viel in den
Kanal schreiben, ohne daß jemals etwas vom Konsumenten
gelesen wird.
|
 | Bei Pipelines unter UNIX liegt die Speicherkapazität
typischerweise bei vier Kilobytes.
|
 | Will der Konsument lesen, ohne daß etwas im Kanal
vorliegt, wird er schlafen gelegt, bis der Produzent
neue Eingaben generiert.
|
 | Umgekehrt wird der Produzent schlafen gelegt, wenn
er den bereits vollständig gefüllten Kanal weiter füllen
möchte.
|
 | Wenn der Produzent die Verbindung schließt, kann der
Konsument noch den bestehenden Inhalt des Kanals auslesen
und beobachtet dann ein Ende der Eingabe.
|
 | Wenn der Konsument die Verbindung schließt, erfährt
dies der Produzent über Fehler beim Schreiben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|

 | Ein bidirektionaler Kommunikationskanal besteht
aus zwei unidirektionalen Kanälen, die zu einer
Verbindung gehören.
|
 | Beispiele: Verbindung zu einem virtuellen Terminal
unter UNIX, Verbindung zu einem Netzwerkdienst.
|
 | Typisch für bidirektionale Kanäle ist ein Dialog,
bei dem die eine Seite Fragen oder Anforderungen stellt
und die andere sie beantwortet.
|
 | Der Dialog zwischen zwei Prozessen wird über ein
Protokoll geregelt, das genau festlegt, wann welche
Partei was in welcher Form über den Kanal schicken
darf.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | In der Ulmer Oberon-Bibliothek offeriert das Modul
Streams eine Schnittstelle zu allen Arten von
Ein- und Ausgabe-Verbindungen.
|
 | Eröffnet wird ein Objekt vom Typ Streams.Stream
durch eine zugehörige Implementierung. Beispiele:
UnixFiles für Dateien unter UNIX,
UnixPipes für Pipelines unter UNIX oder
IPv4TCPSockets für Netzwerkverbindungen über
TCP/IPv4.
|
 | In Abhängigkeit des Streams sind verschiedene
Operationen zulässig wie Lesen, Schreiben, Abfrage
der aktuellen Position und Setzen der Position.
|
 | Bei Verbindungen zu Dateien sind typischerweise
alle vier Operationen möglich. Hingegen unterstützen
Kommunikationskanäle keine Positionen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Auf Wunsch unterstützt das Modul Streams
eine Pufferung, die sehr deutliche Effizienzgewinne
bringen kann. Folgende Pufferungs-Modi werden unterstützt:
| ||||||||||||
 | Wenn Streams.stdin und/oder Streams.stdout
mit einem Terminal unter UNIX verbunden sind, werden sie
zeilenweise gepuffert. Das bedeutet, dass Ausgaben erst
nach der Ausgabe des Zeilentrenners (z.B. durch Write.Ln)
zu sehen sind. Wenn allerdings beide mit einem Terminal
verbunden sind, führt auch eine Einlese-Operation zu einer
Leerung des Ausgabe-Puffers.
| ||||||||||||
 | Bei Dateiverbindungen ist Streams.onebuf sinnvoll.
Bei vielfachen Zugriff unter verschiedenen Positionen
(typisch für Datenbanken) kann auch Streams.bufpool
geeignet sein.
| ||||||||||||
 | Mit der Operation Streams.Flush kann jeweils ein
Ausgabe-Puffer geleert werden.
| ||||||||||||
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF ~UnixFiles.Open(s, filename,
UnixFiles.write + UnixFiles.create,
Streams.onebuf, NIL) THEN
Write.String("Couldn't open "); Write.String(filename);
Write.Line(" for writing!");
RETURN
END;
|
 | UnixFiles.Open erhält fünf Parameter:
| ||||||||||||||||||
 | Der Rückgabe-Wert ist vom Typ BOOLEAN und signalisiert
den Erfolg der Operation.
| ||||||||||||||||||
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgende Modi sind zulässig beim Eröffnen einer Datei:
| UnixFiles.read | Datei nur zum Lesen eröffnen. |
| UnixFiles.write | Datei nur zum Schreiben eröffnen. |
| UnixFiles.rdwr | Datei zum Lesen und Schreiben eröffnen. |
Wird nur einer dieser drei Modi angegeben, schlägt die Operation fehl, wenn die Datei noch nicht existiert. Um das zu ändern, kann einer der beiden folgenden Modi zu einem der oben genannten Modi hinzuaddiert werden, um dieses Verhalten zu ändern:
| UnixFiles.create | Die Datei wird in jedem Falle neu angelegt. Falls die Datei vorher bereits existierte, geht der alte Inhalt vollständig verloren. |
| UnixFiles.condcreate | Die Datei wird nur dann angelegt, falls sie zuvor nicht existiert hat. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE DoIt;
VAR
s: Streams.Stream;
filename: ARRAY 80 OF CHAR;
line: ARRAY 80 OF CHAR;
BEGIN
Write.String("Output file: "); Read.Line(filename);
IF Streams.stdin.count = 0 THEN RETURN END;
IF ~UnixFiles.Open(s, filename,
UnixFiles.write + UnixFiles.create,
Streams.onebuf, NIL) THEN
Write.String("Couldn't open ");
Write.String(filename);
Write.Line(" for writing!");
RETURN
END;
Write.String("Your one-liner: "); Read.Line(line);
IF Streams.stdin.count = 0 THEN RETURN END;
Write.LineS(s, line);
Streams.Release(s); (* close the stream *)
END DoIt;
|
 | Alle bekannten Operationen aus den Modulen Read
und Write lassen sich auch für beliebige Objekte
vom Typ Streams.Stream verwenden.
|
 | Dazu ist jeweils an den Namen der Operation ein ``S''
anzuhängen und als erster Parameter der gewünschte
Stream anzugeben, auf dem die Operation auszuführen ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Bei jedem Objekt vom Typ Streams.Stream gibt es folgende Felder, mit denen der Erfolg der letzten Operation überprüft werden kann:
| count | Liefert die Zahl der umgesetzten Ein- oder Ausgabe-Operationen. Wie diese Zahl zu interpretieren ist, hängt von der Operation selbst ab. Generell bedeutet eine 0 ein Mißerfolg und eine positive Nummer zumindest einen Teilerfolg. |
| error | Wird auf TRUE gesetzt, wenn die letzte Operation nicht erfolgreich war. Dies geschieht jedoch nicht bei einem normalen Eingabe-Ende. |
| errors | Die Gesamtzahl der aufgelaufenen Fehler. |
| eof | Wird bei einem erkannten Eingabe-Ende auf TRUE gesetzt. |
| lasterror | Gibt die Fehlernummer des letzten Fehlers an. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Ein- und Ausgabe-Verbindungen werden vollautomatisch
bei einem natürlichen Programm-Ende geschlossen.
| ||||
 | Beim Schließen werden auch sämtliche Ausgabe-Puffer
geleert.
| ||||
 | Kommt es zu einem Laufzeitfehler, unterbleibt das
automatische Leeren der Ausgabe-Puffer.
| ||||
 | Es gibt zwei Möglichkeiten, selbst eine Verbindung
zu schließen:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Positionen in einer Datei sind vom Typ Streams.Count.
Das sind nicht-negative ganze Zahlen.
|
 | Mit Streams.GetPos kann die aktuelle Position ermittelt
werden.
|
 | Mit Streams.SetPos kann auf eine beliebige gültige
Position gewechselt werden.
|
 | Alternativ können auch Streams.Tell und Streams.Seek
verwendet werden, die jeweils BOOLEAN-Resultate liefern.
Zusätzlich bietet Streams.Seek auch relative
Positionierungen zur aktuellen Position und zum Ende der Datei an.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
dublin$ wc -l cookies 26 cookies dublin$ head -6 cookies % Programming wisdom stolen from % Kernighan and Plauger's % ``The Elements of Programming Style'' Avoid unnecessary branches. Choose a data representation that makes the program simple. Choose variable names that won't be confused. dublin$ FortuneCookie Choose variable names that won't be confused. dublin$ FortuneCookie Write and test a big program in small pieces. dublin$ FortuneCookie Don't comment bad code -- rewrite it. dublin$ |
 | Gegeben sei eine Datei mit Sprüchen. Jeder Spruch
benötigt genau eine Zeile. Hinzu kommen Kommentarzeilen,
die mit einem Prozentzeichen beginnen.
|
 | Eine der Sprüche ist gleichmäßig verteilt auszuwählen
und auszugeben.
|
 | Ansatz: Einmal die Datei vollständig durchlesen und
dabei die Anfangspositionen aller Sprüche merken. Dann
zufällig einen wählen, zu diesem positionieren, ihn
einlesen und ausgeben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CONST maxcookies = 32; TYPE CookiePositions = ARRAY maxcookies OF Streams.Count; CookieFile = RECORD s: Streams.Stream; nofcookies: INTEGER; pos: CookiePositions; END; |
 | Die gesamte Datenstruktur, die für die Auswahl
benötigt wird, ist hier in einem Record zusammengefaßt.
|
 | Der Stream s repräsentiert die Verbindung zur
Datei mit den Sprüchen.
|
 | nofcookies notiert die Zahl der gefundenen Sprüche.
|
 | In dem Array pos werden die Positionen der
Zeilenanfänge der Sprüche notiert.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE OpenCookies(VAR file: CookieFile) : BOOLEAN; PROCEDURE ReadCookie(VAR pos: Streams.Count) : BOOLEAN; VAR line: ARRAY 4 OF CHAR; BEGIN LOOP Streams.GetPos(file.s, pos); Read.LineS(file.s, line); (* end of input file? *) IF file.s.count = 0 THEN RETURN FALSE END; (* skip commented or empty lines *) IF (line[0] # "%") & (line[0] # 0X) THEN RETURN TRUE END; END; END ReadCookie; BEGIN (* OpenCookies *) IF ~UnixFiles.Open(file.s, "cookies", UnixFiles.read, Streams.onebuf, NIL) THEN RETURN FALSE END; file.nofcookies := 0; WHILE (file.nofcookies < maxcookies) & ReadCookie(file.pos[file.nofcookies]) DO INC(file.nofcookies); END; RETURN file.nofcookies > 0 END OpenCookies; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE OpenCookies(VAR file: CookieFile) : BOOLEAN; PROCEDURE ReadCookie(VAR pos: Streams.Count) : BOOLEAN; VAR line: ARRAY 4 OF CHAR; BEGIN LOOP Streams.GetPos(file.s, pos); Read.LineS(file.s, line); (* end of input file? *) IF file.s.count = 0 THEN RETURN FALSE END; (* skip commented or empty lines *) IF (line[0] # "%") & (line[0] # 0X) THEN RETURN TRUE END; END; END ReadCookie; BEGIN (* OpenCookies *) |
 | Neben lokalen Variablen kann es auch lokale Prozeduren
geben.
|
 | Lokale Prozeduren sind nur innerhalb der sie umgebenden
Prozedur sichtbar.
|
 | Lokale Prozeduren dürfen auf die Parameter und Variablen
der sie umgebenden Prozedur zugreifen. (Hier konkret auf
file).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE PrintCookie(file: CookieFile; index: INTEGER); VAR cookie: ARRAY 512 OF CHAR; BEGIN Streams.SetPos(file.s, file.pos[index]); Read.LineS(file.s, cookie); Write.Line(cookie); END PrintCookie; |
 | PrintCookie positioniert die Dateiverbindung
auf den index-ten Spruch (von 0 an zählend)
und gibt diesen aus.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE DoIt;
VAR
file: CookieFile;
selected: INTEGER; (* index of selected cookie *)
BEGIN
IF ~OpenCookies(file) THEN
Write.String("I am sorry as I am unable ");
Write.Line("to locate any cookies!");
RETURN
END;
selected := SHORT(RandomGenerators.Val(0,
file.nofcookies-1));
PrintCookie(file, selected);
END DoIt;
|
 | Das Hauptprogramm wurde hier in die Prozedur DoIt
verlagert, damit ein Verzicht auf globale Variablen möglich
ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Eröffnen einer Datei |
 | Lese- und Schreib-Operationen |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Datenstruktur von FortuneCookie |
 | Durchgang durch die Datei |
 | Lokale Prozeduren |
 | Positionierung in einer Datei |
 | Hauptteil der Spruchauswahl |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE EchoArgs; IMPORT Args := UnixArguments, Write; PROCEDURE EchoArguments; VAR arg: ARRAY 512 OF CHAR; BEGIN WHILE Args.GetArg(arg) DO Write.Line(arg); END; END EchoArguments; BEGIN EchoArguments; END EchoArgs. |
 | In einer Shell unter UNIX können neben dem
Programmnamen noch weitere Argumente an ein Programm
übergeben werden.
|
 | In Abhängigkeit von der Programmiersprache können
dann die Argumente innerhalb eines Programms verarbeitet
werden.
|
 | Das Modul SysArgs dient im Ulmer Oberon-System
als systemnahe Schnittstelle. Sehr viel komfortabler ist hier
UnixArguments, weil damit auch die üblichen Konventionen
unter UNIX unterstützt werden. Args dient als allgemeine
Schnittstelle, wenn Argumente auch von anderen Quellen zu
berücksichtigen sind.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
dublin$ cat file1 Dies ist der Inhalt von file1. dublin$ cat file2 Der Inhalt von file2 geht ueber zwei Zeilen. dublin$ cat file3 Und hier ist der Inhalt von file3. dublin$ cat file1 file2 file3 Dies ist der Inhalt von file1. Der Inhalt von file2 geht ueber zwei Zeilen. Und hier ist der Inhalt von file3. dublin$ |
 | Aufgabe: Auf der Kommandozeilen können beliebig viele
Dateinamen angegeben werden. Alle sind hintereinander
zu öffnen und deren Inhalt ist auf die Standardausgabe
zu kopieren.
|
 | Wird auf der Kommandozeile überhaupt keine Datei
angegeben, wird von der Standard-Eingabe zur Standard-Ausgabe
kopiert.
|
 | Vorbild ist das Kommando cat, das für
concatenate steht.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* output all input files in the given order to stdout; take stdin if no input files are given *) MODULE Concatenate; IMPORT Args := UnixArguments, Process, Streams, UnixFiles, Write; PROCEDURE Copy(in, out: Streams.Stream) : BOOLEAN; (* copy all bytes from in to out; return FALSE in case of errors *) (* ... *) END Copy; PROCEDURE ProcessFiles; (* ... *) END ProcessFiles; BEGIN ProcessFiles; END Concatenate. |
 | Das Programm wird aufgeteilt in die Prozedur Copy, die
von einer Eingabe-Verbindung zu einer Ausgabe-Verbindung
kopiert und die Prozedur ProcessFiles, die durch
sämtliche Dateinamen auf der Kommandozeile geht,
die angegebenen Dateien eröffnet und Copy aufruft.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Copy(in, out: Streams.Stream) : BOOLEAN; (* copy all bytes from in to out; return FALSE in case of errors *) VAR ch: CHAR; BEGIN WHILE Streams.ReadByte(in, ch) DO IF ~Streams.WriteByte(out, ch) THEN RETURN FALSE END; END; RETURN in.eof END Copy; |
 | Mit Streams.ReadByte und Streams.WriteByte
kann byte-weise kopiert werden.
|
 | Wichtig ist, daß bei Fehlern sofort mit einem
RETURN FALSE abgebrochen wird.
|
 | Wenn das Einlesen an einem Fehler scheitert, endet die
WHILE-Schleife und in.error ist TRUE,
während in.eof noch FALSE ist.
|
 | Klappt die Ausgabe nicht, wird die Prozedur mitten in
der WHILE-Schleife mit einem RETURN FALSE
verlassen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE ProcessFiles; VAR pathname: ARRAY 512 OF CHAR; in: Streams.Stream; BEGIN IF Args.GetArg(pathname) THEN REPEAT IF ~UnixFiles.Open(in, pathname, UnixFiles.read, Streams.onebuf, NIL) THEN Write.StringS(Streams.stderr, pathname); Write.StringS(Streams.stderr, ": cannot be "); Write.StringS(Streams.stderr, "opened for "); Write.LineS(Streams.stderr, "reading"); Process.Exit(Process.indicateFailure); END; IF ~Copy(in, Streams.stdout) THEN Write.StringS(Streams.stderr, "write error "); Write.StringS(Streams.stderr, "while copying "); Write.LineS(Streams.stderr, pathname); END; Streams.Release(in); UNTIL ~Args.GetArg(pathname); ELSE IF ~Copy(Streams.stdin, Streams.stdout) THEN Write.StringS(Streams.stderr, "write error "); Write.StringS(Streams.stderr, "while copying "); Write.LineS(Streams.stderr, "standard input"); END; END; END ProcessFiles; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF ~UnixFiles.Open(in, pathname, UnixFiles.read, Streams.onebuf, NIL) THEN Write.StringS(Streams.stderr, pathname); Write.StringS(Streams.stderr, ": cannot be "); Write.StringS(Streams.stderr, "opened for "); Write.LineS(Streams.stderr, "reading"); Process.Exit(Process.indicateFailure); END; |
 | Fehler sollten nicht nach Streams.stdout
geschrieben werden, sondern nach Streams.stderr,
damit sich Fehlermeldungen nicht unbemerkt in die
normale Ausgabe eines Programms mischen.
|
 | Dies ist insbesondere relevant, wenn die Standard-Ausgabe
in eine Datei umgelenkt wird.
|
 | Wenn etwas schief geht, sollte das Programm sich so
verabschieden, daß die Umgebung weiß, daß es nicht
erfolgreich war. Process.Exit terminiert das Programm
mit dem angegebenen Exit-Code. 0 bedeutet hier Erfolg und
jedes andere Resultat Mißerfolg.
|
dublin$ Concatenate /unbekannte/datei >/tmp/out /unbekannte/datei: cannot be opened for reading dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
thales$ mkfile 10m 10m thales$ time cp 10m 10m.2 real 0m1.17s user 0m0.01s sys 0m0.16s thales$ time Concatenate 10m >10m.2 real 0m8.48s user 0m5.62s sys 0m0.22s thales$ |
 | Trotz gepufferter Ein- und Ausgabe ist diese Lösung
benötigt diese Lösung ein mehrfaches der Zeit im
Vergleich zum cp-Kommando.
|
 | Das liegt primär daran, daß byte-weise kopiert
wird, d.h. für jedes einzelne Byte gibt es die
Prozeduraufrufe Streams.ReadByte und Streams.WriteByte.
|
 | Es wäre sehr viel effizienter, in größeren Einheiten
zu arbeiten. Dann gibt es nur einen Bruchteil der Prozeduraufrufe.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Copy(in, out: Streams.Stream) : BOOLEAN; (* copy all bytes from in to out; return FALSE in case of errors *) VAR ch: CHAR; BEGIN RETURN Streams.Copy(in, out, -1) END Copy; |
 | Das Streams-Modul bietet hier die Prozedur Copy
an, mit der eine bestimmte Anzahl von Bytes oder alle (bei
Angabe von -1) von einer Verbindung zur anderen kopiert werden.
|
 | Diese Prozedur liest und schreibt in größeren Quantitäten (8k).
|
 | Das führt zu einer deutlichen Verbesserung:
|
thales$ time Concatenate 10m >10m.2 real 0m8.48s user 0m5.62s sys 0m0.22s thales$ time Concatenate2 10m >10m.2 real 0m1.72s user 0m1.32s sys 0m0.23s thales$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
IF ~UnixMappedFiles.Open(in, pathname, UnixMappedFiles.read, NIL) THEN Write.StringS(Streams.stderr, pathname); Write.StringS(Streams.stderr, ": cannot be "); Write.StringS(Streams.stderr, "opened for "); Write.LineS(Streams.stderr, "reading"); Process.Exit(Process.indicateFailure); END; |
 | Das cp-Kommando verwendet aber noch weitere Tricks,
um so überragend schnell zu werden.
Einer der Tricks vermeidet das Einlesen, indem die
Eingabe-Dateien in den Adreßraum des kopierenden Programms
gelegt werden.
|
 | In Oberon kann dieser Trick verwendet werden, wenn
an Stelle von UnixFiles das Modul UnixMappedFiles
verwendet wird. Das funktioniert aber nur für reguläre Dateien.
|
thales$ time Concatenate2 10m >10m.2 real 0m1.72s user 0m1.32s sys 0m0.23s thales$ time Concatenate3 10m >10m.2 real 0m1.53s user 0m1.09s sys 0m0.30s thales$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
(* set defaults *)
numbered := FALSE;
silent := FALSE;
(* set usage line *)
Args.Init("[-n] [-s] {file}");
(* process options *)
WHILE Args.GetFlag(option) DO
CASE option OF
| "n": numbered := TRUE;
| "s": silent := TRUE;
ELSE
Args.Usage;
END;
END;
|
 | Das originale cat-Kommando unterstützt einige
Optionen, wovon hier zwei beispielhaft implementiert werden:
| ||||
 | Mit Args.Init wird die Kommandozeilen-Syntax
spezifiziert, die ggf. später von Args.Usage
ausgegeben wird.
| ||||
 | Args.GetFlag holt die nächste Option von
der Kommandozeile. Diese Prozedur liefert FALSE,
sobald alle Optionen abgearbeitet sind. Dann bleiben
nur noch die Dateiargumente (ohne führenden Bindestrich)
übrig.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Aufgabe: Zu implementieren ist ein Werkzeug nach dem
Vorbild von cut, das einzelne Felder aus der Eingabe
selektiert.
| ||||
 | Dieses Kommando unterstützt die Konvention der kleinen
Datenbanken im Textformat unter UNIX:
| ||||
 | Eine ähnliche Konvention ist in der Windows-Welt auch unter
dem Begriff CSV (comma separated values) bekannt.
| ||||
 | Zu unterstützende Optionen:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
fieldsep: CHAR; (* field separator *) delim: ARRAY 4 OF CHAR; (* used to read fieldsep *) selected: SET; (* selected set of fields *) fieldnum: INTEGER; (* used to read a field number *) arg: Streams.Stream; (* command line argument as stream *) option: CHAR; (* current command line option *) in: Streams.Stream; (* input stream *) pathname: ARRAY 512 OF CHAR; (* name of an input file *) |
 | Der Parameter einer Option kann mit Args.FetchString
oder Args.Fetch geholt werden.
|
(* set defaults *)
fieldsep := ASCII.tab; selected := {};
(* process options *)
Args.Init("[-d delim] {-f fieldno} {file}");
WHILE Args.GetFlag(option) DO
CASE option OF
| "d": Args.FetchString(delim); fieldsep := delim[0];
| "f": Args.Fetch(arg); Read.IntS(arg, fieldnum);
IF (arg.count > 0) & (fieldnum >= 1) &
(fieldnum <= MAX(SET) + 1) THEN
INCL(selected, fieldnum-1);
ELSE
Args.Usage;
END;
ELSE
Args.Usage;
END;
END;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CASE option OF | "d": Args.FetchString(delim); fieldsep := delim[0]; | "f": Args.Fetch(arg); Read.IntS(arg, fieldnum); IF (arg.count > 0) & (fieldnum >= 1) & (fieldnum <= MAX(SET) + 1) THEN INCL(selected, fieldnum-1); ELSE Args.Usage; END; ELSE Args.Usage; END; |
 | Args.Fetch eröffnet den Parameter als Stream, von
dem anschließend (z.B. mit Read.IntS) gelesen werden kann.
|
 | Ein mit Args.Fetch geöffneter Stream muß nicht
explizit geschlossen werden, da das nächste Args.Fetch
den vorher genutzten Stream automatisch schließt.
|
 | Args.FetchString kopiert den Parameter in ein
CHAR-Array.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Felder können unter Berücksichtigung von Feldtrennern
und Zeilenterminatoren mit Read.Field
bzw. Read.FieldS eingelesen werden.
| ||||||
 | Die Operation von Read.Field hängt von folgenden
impliziten Parametern ab, die alle über das Modul
StreamDisciplines gesetzt werden können:
| ||||||
 | Folgen von Feldtrennern, die zugleich auch als Leerzeichen
gelten, werden zu einem Trenner zusammengefaßt.
| ||||||
 | Leerzeichen, die ein Feld umgeben, werden entfernt.
| ||||||
 | Read.Field überliest nie den Zeilentrenner,
sondern liefert FALSE am Zeilenende. Der Zeilentrenner
kann dann mit Read.Ln übersprungen werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE CutAndCopy(in: Streams.Stream; out: Streams.Stream; selected: SET; (* selected fields *) fieldsep: CHAR) : BOOLEAN; VAR field: ARRAY 512 OF CHAR; fieldno: INTEGER; insertsep: BOOLEAN; fieldseps: Sets.CharSet; BEGIN Sets.InitSet(fieldseps); Sets.InclChar(fieldseps, fieldsep); StreamDisciplines.SetFieldSepSet(in, fieldseps); LOOP fieldno := 0; insertsep := FALSE; WHILE Read.FieldS(in, field) DO IF fieldno IN selected THEN IF insertsep THEN Write.CharS(out, fieldsep); ELSE insertsep := TRUE; END; Write.StringS(out, field); END; INC(fieldno); END; IF in.eof THEN RETURN TRUE END; IF in.error THEN RETURN FALSE END; Read.LnS(in); IF in.eof THEN RETURN TRUE END; IF in.error THEN RETURN FALSE END; Write.LnS(out); IF out.errors > 0 THEN RETURN FALSE END; END; END CutAndCopy; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Sets.InitSet(fieldseps); Sets.InclChar(fieldseps, fieldsep); StreamDisciplines.SetFieldSepSet(in, fieldseps); |
 | Das Modul Sets unterstützt Mengen, die umfangreicher
sind als SET.
|
 | Sets.CharSet ist ein Mengentyp, der beliebige
Zeichen (also CHAR) aufnehmen kann. fieldseps
ist hier von diesem Typ.
|
 | Mit Sets.InitSet wird eine Menge zu der leeren Menge
initialisiert.
|
 | Mit Sets.InclChar wird ein Element in eine Menge
aufgenommen (analog zu INCL).
|
 | Die Menge der Feldtrenner für einen Stream wird mit
StreamDisciplines.SetFieldSepSet festgelegt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
fieldno := 0; insertsep := FALSE; WHILE Read.FieldS(in, field) DO IF fieldno IN selected THEN IF insertsep THEN Write.CharS(out, fieldsep); ELSE insertsep := TRUE; END; Write.StringS(out, field); END; INC(fieldno); END; |
 | Da Read.FieldS nicht den Zeilentrenner überspringt,
können bequem alle Felder einer Zeilen mit einer
WHILE-Schleife abgearbeitet werden.
|
 | Zu beachten ist hier, daß bei einer unzureichenden
Länge des Arrays field Feldinhalte stillschweigend
abgeschnitten werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Gegeben seien n Datensätze R1 ··· Rn vom gleichen Typ,
die im Hauptspeicher (z.B. in einem Array) liegen.
| ||||||
 | Die Datensätze haben ein oder mehrere Felder, die
zusammen die Schlüssel K1 ··· Kn bilden.
| ||||||
 | Für die Schlüssel gibt es eine vollständige
Ordnungsrelation <=.
| ||||||
 | Eine Ordnungs-Relation <= ist vollständig, wenn
| ||||||
 | Gesucht wird eine Permutation p(1) ··· p(n), so daß
gilt: Kp(1) <= Kp(2) <= ··· <= Kp(n). | ||||||
 | Literatur: ``The Art of Computer Programming'' von
Donald E. Knuth, Volume 3, ``Sorting and Searching''.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Es wird von internen Sortierverfahren gesprochen, wenn
alle zu sortierenden Datensätze im Hauptspeicher liegen.
| ||||||||
 | Es gibt sehr viele interne Sortierverfahren, die aber
praktisch alle in eine der folgenden Kategorien fallen:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Viele Sortierverfahren können sinnvoll im Einsatz sein. Die Auswahl hängt u.a. von folgenden Kriterien ab:
 | Wieviele Datensätze sind zu sortieren?
|
 | Wie effizient sind die einzelnen benötigten
Zugriffsoperationen für die gegebene Datenstruktur?
Wir kennen bislang Arrays, bei denen der Zugriff auf
das i-te Element sehr effizient ist, aber das
Einfügen zu aufwendigen Verschiebeoperationen führt.
|
 | Sind die Datensätze bereits vorsortiert oder nahezu
sortiert? Oder ist von einer zufälligen Permutation
auszugehen?
|
 | Wie groß ist der Wertebereich der Schlüssel?
|
 | Wie aufwendig sind Vergleichsoperationen?
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Folgendes Sortierverfahren findet sich im Band 3 des Werks
``The Art of Computer Programming'' von D. Knuth:
| ||||||||
 | Algorithm C (Comparison counting).
This algorithm sorts R1, ···, RN on the keys
K1, ···, KN by maintaining an auxiliary table
COUNT[1], ···, COUNT[N ]
to count the number of keys less than a given key. After
the conclusion of the algorithm, COUNT[j] + 1
will specify the final position of record Rj.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE ComparisonCounting; IMPORT Read, Streams, Write; CONST maxitems = 128; TYPE Item = INTEGER; Items = ARRAY maxitems OF Item; PROCEDURE Sort(VAR items: Items; nofitems: INTEGER); (* ... *) END Sort; PROCEDURE ReadItems(VAR items: Items) : INTEGER; (* ... *) END ReadItems; PROCEDURE WriteItems(items: Items; nofitems: INTEGER); (* ... *) END WriteItems; PROCEDURE DoIt; (* ... *) END DoIt; BEGIN DoIt; END ComparisonCounting. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Sort(VAR items: Items; nofitems: INTEGER); VAR myitems: Items; (* local copy of items *) count: ARRAY maxitems OF INTEGER; i, j: INTEGER; (* indices of items and myitems *) BEGIN (* initialize count array *) i := 0; WHILE i < nofitems DO count[i] := 0; INC(i); END; (* work on a local copy of items *) myitems := items; (* compare all items with each other and count *) i := nofitems-1; WHILE i >= 1 DO j := i-1; WHILE j >= 0 DO IF myitems[j] <= myitems[i] THEN INC(count[i]); ELSE INC(count[j]); END; DEC(j); END; DEC(i); END; (* update items according to count *) i := 0; WHILE i < nofitems DO items[count[i]] := myitems[i]; INC(i); END; END Sort; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Generell ist es sehr sinnvoll, den Rechenzeitaufwand eines
Algorithmus in Abhängigkeit von n (Datenumfang oder
andere entscheidende Problemgröße) abzuschätzen.
| ||||||||||||||
 | Hierzu eignet sich die von Paul Bachmann 1894 eingeführte
O-Notation an: g(n) = O(f(n)) für n ∈ N, falls ∃ M, n0 ∈ N, so daß gilt | g(n) | <= | M f(n) | ∀ n >= n0. | ||||||||||||||
 | Einige Beispiele:
| ||||||||||||||
 | Die O-Notation hilft insbesondere bei der Beurteilung, ob
ein Algorithmus für großes n noch geeignet ist bzw.
erlaubt einen Effizienz-Vergleich zwischen verschiedenen
Algorithmen für große n.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sei n die Zahl der zu sortierenden Datensätze
(repräsentiert durch die Variable nofitems im Programm).
| ||||||||||||||||||
 | Wir haben in der Prozedur Sort drei äußere Schleifen.
| ||||||||||||||||||
 | Bei der ersten und letzten Schleife ist der Aufwand
jeweils O(n), zusammen also O(2n), was wiederum O(n)
entspricht, da bei der O-Notation konstante Faktoren einfach
weggestrichen werden können.
| ||||||||||||||||||
 | Die innerste Schleife benötigt im ersten Durchlauf
N-1 Schritte, im zweiten Durchlauf N-2 Schritte und
zuletzt nur noch einen Schritt. In der Summe ergibt das
| ||||||||||||||||||
 | Die Summe für den gesamten Aufwand bleibt dann bei O(n2).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Folgendes Sortierverfahren findet sich im Band 3 des Werks
``The Art of Computer Programming'' von D. Knuth:
| ||||||||||||
 | Algorithm D (Distribution counting).
Assuming that all keys are integers in the range
u <= Kj <= v for 1 <= j <= N,
this algorithm sorts the records R1, ..., RN
by making use of an auxiliary table
COUNT[u ], ..., COUNT[v ].
At the conclusion of the algorithm the records are
moved to an output area S1, ..., SN in the
desired order.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sei n die Zahl der zu sortierenden Datensätze und
m := v - u + 1 die Länge des Intervalls [u,v].
|
 | D1: O(n).
|
 | D2/D3: O(n).
|
 | D4: O(m).
|
 | D5/D6: O(n).
|
 | In der Summe ergibt dies
3 · O(n) + O(m) = O(n + m).
|
 | Dieses Sortierverfahren ist überraschend schnell,
wenn der Wertebereich der Schlüssel sehr klein ist.
|
 | Es ist aber nicht geeignet für große m,
insbesondere wenn m >> n.
|
 | Es kann aber verwendet werden, um recht rasch eine
große Datenmenge entsprechend einer Partitionierung
des Schlüsselraums (z.B. aufgrund eines Prefix wie
beispielsweise dem ersten Buchstaben) zu sortieren.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Sort(VAR items: Items; min, max: INTEGER; nofitems: INTEGER); VAR myitems: Items; (* local copy of items *) count: ARRAY maxintervallen OF INTEGER; i, j: INTEGER; (* indices of items and myitems *) BEGIN (* D1 *) i := 0; WHILE i < max - min + 1 DO count[i] := 0; INC(i); END; (* make local copy of items *) myitems := items; (* D2/D3 *) i := 0; WHILE i < nofitems DO INC(count[myitems[i] - min]); INC(i); END; (* D4 *) i := 1; WHILE i < max - min + 1 DO INC(count[i], count[i-1]); INC(i); END; (* D5/D6 *) j := nofitems-1; WHILE j >= 0 DO i := count[myitems[j] - min]; items[i-1] := myitems[j]; DEC(count[myitems[j] - min]); DEC(j); END; END Sort; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Folgendes Sortierverfahren findet sich im Band 3 des Werks
``The Art of Computer Programming'' von D. Knuth:
| ||||||||
 | Algorithm B (Bubble sort).
Records R1, ..., RN are rearranged in place;
after sorting is complete their keys will be in
order, K1 <= ··· <= KN.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Sei n die Zahl der zu sortierenden Datensätze.
|
 | Im schlimmsten Fall ist K1 > Ki für alle
i = 2, ..., i = n.
|
 | Dann wird im ersten Durchlauf von B2 innerhalb von B3
u.a. R1 mit R2 vertauscht, im zweiten Durchlauf von B2
kommt es u.a. zum Tausch von R2 mit R3 usw.
|
 | Erst nach n-1 Durchläufen landet der ursprüngliche
Datensatz R1 in Rn.
|
 | Das ergibt entsprechenden quadratischen Aufwand von O(n2).
|
 | Falls jedoch die Datensätze bereits sortiert vorliegen,
reduziert sich der Aufwand auf O(n).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seite im Skript |
 | Argumente aus der Kommandozeile |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Rahmen des Kopierprogramms |
 | Kopierprozedur |
 | Abarbeiten der Kommandozeile |
 | Fehlerbehandlung |
 | Schnelleres Kopieren |
 | Schnelleres Kopieren II |
 | Verarbeiten von Optionen |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Optionen mit Parametern II |
 | Optionen mit Parametern III |
 | Einlesen von Feldern II |
 | Einlesen von Feldern III |
 | Einlesen von Feldern IV |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Sort(VAR items: Items; nofitems: INTEGER); VAR bound: INTEGER; (* items[0] .. items[bound] are possibly unsorted; items[bound+1] .. items[nofitems-1] are sorted and at their final positions *) t: INTEGER; (* highest t where items[t] is possibly not yet sorted *) j: INTEGER; (* index of items *) item: Item; (* temporary variable for swapping *) BEGIN bound := nofitems - 1; (* B1 *) REPEAT (* B2 *) j := 0; t := 0; WHILE j < bound DO (* B3 *) IF items[j] > items[j+1] THEN item := items[j]; items[j] := items[j+1]; items[j+1] := item; t := j; END; INC(j); END; bound := t; (* B4 *) UNTIL bound = 0; END Sort; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Sortierprozeduren, die wir bislang gesehen haben,
hatten eine Reihe von Abhängigkeiten vom zu sortierenden
Datentyp:
| ||||||
 | Dies hat zur Folge, daß bei mehreren Sortier-Problemen
auch mehrere individuelle Sortier-Prozeduren geschrieben
werden müssen, die jeweils an die individuellen Typen
angepasst sind.
| ||||||
 | Diese Problematik ließe sich vermeiden, wenn Zugriffe
auf die Datensätze und Vergleichs-Operationen von der
Sortierprozedur getrennt werden könnten.
| ||||||
 | Das ließe sich lösen, wenn entsprechende Operationen
als Parameter an die Sortier-Prozedur übergeben werden
könnten.
| ||||||
 | Das ist möglich mit Hilfe von Prozedur-Typen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
TYPE GreaterThanProc = PROCEDURE (i, j: INTEGER) : BOOLEAN; (* return true if item i is > item j *) ExchangeProc = PROCEDURE (i, j: INTEGER); (* swap items i and j *) |
 | Deklarationen von Prozedurtypen gleichen den
gewohnten Prozedurköpfen. Nur der Prozedurname
fällt weg.
|
 | Danach können Variablen oder Parameter von
so einem Typ deklariert werden.
|
 | Dann können an diese Variablen oder Parameter
Prozeduren dieses Typs zugewiesen oder übergeben
werden.
|
PROCEDURE Sort(gt: GreaterThanProc; exchange: ExchangeProc; nofitems: INTEGER); |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE IntegerGreaterThan(i, j: INTEGER) : BOOLEAN; BEGIN RETURN integers[i] > integers[j] END IntegerGreaterThan; PROCEDURE ExchangeIntegers(i, j: INTEGER); VAR tmp: Integer; BEGIN tmp := integers[i]; integers[i] := integers[j]; integers[j] := tmp; END ExchangeIntegers; |
 | Die Prozeduren IntegerGreaterThan und
ExchangeIntegers passen genau zu den
Prozedurtypen GreaterThanProc und
ExchangeProc.
|
 | Entsprechend können diese Prozedur als Parameter
an Sort übergeben werden:
|
PROCEDURE SortIntegers; VAR nofitems: INTEGER; BEGIN nofitems := ReadIntegers(integers); IF nofitems > 0 THEN Sort(IntegerGreaterThan, ExchangeIntegers, nofitems); WriteIntegers(integers, nofitems); END; END SortIntegers; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Sort(gt: GreaterThanProc; exchange: ExchangeProc; nofitems: INTEGER); VAR bound: INTEGER; (* items[0] .. items[bound] are possibly unsorted; items[bound+1] .. items[nofitems-1] are sorted and at their final positions *) t: INTEGER; (* highest t where items[t] is possibly not yet sorted *) j: INTEGER; (* index of items *) BEGIN bound := nofitems - 1; REPEAT (* B2 *) j := 0; t := 0; WHILE j < bound DO (* B3 *) IF gt(j, j+1) THEN exchange(j, j+1); t := j; END; INC(j); END; (* B4 *) bound := t; UNTIL bound = 0; END Sort; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Bei Prozedurtypen gibt es eine wesentliche Einschränkung
in Oberon: Es dürfen nur globale Prozeduren an Variablen
oder Parameter eines Prozedurtyps zugewiesen oder übergeben
werden.
|
 | Das bedeutet, daß der Prozedur nur ihre Parameter und
globale Variablen zur Verfügung stehen.
|
 | Da wir die Sortierprozedur unabhängig von dem zu
sortierenden Typ halten wollten, können wir das zu
sortierende Array nicht als Parameter übergeben.
|
 | Daraus folgt, daß die zu sortierenden Arrays in
globalen Variablen untergebracht werden müssen.
|
 | Es gibt Programmiersprachen, die auch lokale Prozeduren
zulassen. Diese sorgen dann dafür, daß die Umgebung einer
lokalen Prozedur auch erhalten bleibt, wenn es eine entsprechende
Referenz auf eine lokale Prozedur gibt. Beispiele dafür sind
Scheme und Perl.
|
 | In Sprachen mit objekt-orientierten Techniken wird das
Problem typischerweise anders gelöst. In Oberon geschieht
dies durch sogenannte Typ-Erweiterungen. Mehr dazu im
nächsten Semester.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE SortStrings; VAR nofitems: INTEGER; BEGIN nofitems := ReadStrings(strings); IF nofitems > 0 THEN Sort(StringGreaterThan, ExchangeStrings, nofitems); WriteStrings(strings, nofitems); END; END SortStrings; |
 | Die gewonnene Flexibilität durch Prozedurtypen
ermöglicht es jetzt, die gleiche Sortierprozedur
für unterschiedliche Sortierprobleme zu lösen.
|
 | Entsprechend der Optionen auf
der Kommandozeile können nun unterschiedliche
Typen und Kriterien ausgewählt werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Wenn wir jeden zu sortierenden Datensatz
mit nahezu jeden anderen Datensatz vergleichen,
erreichen wir einen Aufwand von O(n2).
|
 | Ein besseres Sortierverfahren muß also
insbesondere die Zahl der Vergleiche reduzieren.
Das ist nur möglich, wenn nicht nur unmittelbare
Nachbarn miteinander verglichen werden.
|
 | Hier erscheint es sinnvoll, kleinere Teilmengen
der Datensätze isoliert zu sortieren.
|
 | Um die Gesamtmenge der Datensätze zu sortieren
ist dann entweder einer Vorsortierung oder
eine Nachsortierung notwendig.
|
 | Ein Beispiel für einen Algorithmus mit Vorsortierung
ist der sogenannte Quicksort-Algorithmus von C. A. R. Hoare.
|
 | Ein (hier nicht weiter behandeltes) Beispiel mit
Nachsortierung ist der von Knuth ``merge exchange sort'' genannte
Algorithmus von K. E. Batcher.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Gegeben seien die Schlüssel K1,...,Kn.
| ||||||
 | Eine Vorsortierung zerlegt die Schlüssel in
einzelne Partitionen. Bei Quicksort findet immer
eine Zerlegung in zwei Partitionen statt.
| ||||||
 | Ein beliebiger Schlüssel P
(das sogenannte Pivot-Element) aus K1 ... Kn ist auszuwählen
(beispielsweise K1).
| ||||||
 | Dann wird K so partitioniert, daß es i,j aus 1..n gibt,
so daß gilt
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Die Nachsortierung kann darin bestehen, daß eine
Partitionierung für beide Bereiche erneut vorgenommen
wird.
|
 | Wenn kein oder nur ein Schlüssel vorliegt, ist
keine weitere Partitionierung notwendig.
|
 | Wenn zwei Schlüssel partitioniert werden, liegt
die Menge danach sortiert vor.
|
 | Es ist also möglich, nur mit Partitionierungen
auszukommen.
|
 | Alternativ kann auf ein einfaches Sortierverfahren
zurückgegriffen werden, wenn die Restmenge genügend
klein ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
i := first; j := last; REPEAT WHILE gt(pivot, i) DO INC(i); END; WHILE gt(j, pivot) DO DEC(j); END; IF i <= j THEN Exchange(i, j, pivot); INC(i); DEC(j); END; UNTIL i > j; |
 | Die Variablen first und last geben
den zu sortierenden Bereich an.
|
 | Da wir partitionierte Bereiche erneut partionieren
möchten, liegen diese nur zu Beginn bei 1 und nofitems.
|
 | Der Index pivot zeigt auf das ausgewählte Pivot-Element.
|
 | Der Index i wird dann, beginnend von first,
aufwärts gezählt, während der Index j
heruntergezählt wird.
|
 | Alle Schlüssel werden mit dem Pivot-Element verglichen.
Dabei suchen wir ein Paar i,j mit Ki <= P und
Kj >= P. Dies wird getauscht.
|
 | Die Partitionierung ist beendet, sobald i > j, d.h.
beide Indizes ``überkreuzt'' sind.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE Exchange(i, j: INTEGER; VAR pivot: INTEGER); (* update the index of the pivot element if necessary *) BEGIN exchange(i, j); IF pivot = i THEN pivot := j; ELSIF pivot = j THEN pivot := i; END; END Exchange; |
 | Wenn ein Austausch stattfindet, der den Index
des Pivot-Elements betrifft, muß dieser aktualisiert
werden.
|
 | Andernfalls kommt es implizit zu einem Wechsel
des Pivot-Elements.
|
 | Dies wäre harmlos, wenn zu Beginn pivot
dem Wert von first gleichen würde. Bei
jeder anderen Wahl könnte das jedoch fatal sein.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Wenn wir partitionierte Bereiche wiederum dem
gleichen Partitionierungsverfahren unterwerfen
möchten, müssen wir berücksichtigen, daß
nach jeder Partitionierung zwei neue Partitionierungen
entstehen.
|
 | Das kann nur entfallen, wenn die Partionierungen
genügend klein werden (0 oder 1 Schlüssel).
|
 | Eine einfache Schleife genügt dafür nicht, da
wir uns nur eine der beiden neu entstandenen Partitionen
als nächstes vorknöpfen können.
|
 | Eine Lösung ist die Verwendung eines Stapels mit
zu erledigenden Arbeiten. Ein Arbeitsauftrag kann hierbei
vollständig mit zwei Indizes für den sortierenden
Bereich spezifiziert werden (first und last):
|
TYPE Job = RECORD first, last: INTEGER; END; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
CONST stacklen = maxitems; VAR jobs: ARRAY stacklen OF Job; top: INTEGER; |
 | Wenn uns die Reihenfolge der Abarbeitung von
Aufträgen egal ist, ist ein Stapel als Datenstruktur ideal.
|
 | Ein Stapel besteht aus einem Array und einem zugehörigen
Index, der den Füllgrad des Arrays angibt. Letzteres entspricht
genau der Zahl der gespeicherten Aufträge.
|
 | Wenn ein Auftrag hinzukommt, wird dieser bei jobs[top]
untergebracht und top anschließend um eins erhöht.
|
 | Aufträge gibt es, solange der Index positiv ist. Ein
Auftrag wird genommen indem zuerst top um eins gesenkt
wird und dann jobs[top] verwendet wird.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE PushJob(first, last: INTEGER); BEGIN ASSERT(top < stacklen); jobs[top].first := first; jobs[top].last := last; INC(top); END PushJob; PROCEDURE FetchJob(VAR first, last: INTEGER) : BOOLEAN; BEGIN IF top = 0 THEN RETURN FALSE END; DEC(top); first := jobs[top].first; last := jobs[top].last; RETURN TRUE END FetchJob; |
 | PushJob übernimmt einen Auftrag und
legt ihn ganz oben auf den Stapel.
|
 | FetchJob liefert FALSE, falls kein
Auftrag mehr vorliegt. Ansonsten wird der Auftrag
über die beiden Referenz-Parameter first und
last zurückgegeben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
top := 0; (* initialize job stack *) PushJob(0, nofitems-1); WHILE FetchJob(first, last) DO (* sort all items with indices first..last *) IF first < last THEN (* select pivot element *) pivot := (first + last) DIV 2; (* divide ... *) i := first; j := last; REPEAT WHILE gt(pivot, i) DO INC(i); END; WHILE gt(j, pivot) DO DEC(j); END; IF i <= j THEN Exchange(i, j, pivot); INC(i); DEC(j); END; UNTIL i > j; (* ... and conquer *) PushJob(first, j); PushJob(i, last); END; END; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Nehmen wir an, daß es uns jeweils gelänge ein
Pivot-Element auszuwählen, das genau dem Median
der Schlüssel des zu partitionierenden Bereiches
entspricht.
|
 | Dann würde eine Partitionierung immer zwei
gleich große Partitionen erzeugen.
|
 | Nach log2 n Partitionierungen landen wir
dann bei Partitionen mit einem Element.
|
 | Der Partitionierungsaufwand ist linear abhängig
von der Größe des zu partitionierenden Bereichs.
|
 | Zusammengerechnet ergibt das immer O(n).
|
 | Beides miteinander multipliziert ergibt dann
O(n log2 n).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Das war der Idealfall!
|
 | Nehmen wir an, daß das Pivot-Element jeweils
am Rand liegt.
|
 | Dann haben wir eine Partition mit einem Element
und eine mit dem Rest.
|
 | Dann benötigen wir n-1 Partitionierungen.
|
 | Das führt zu einem Gesamtaufwand von O(n2).
|
 | Leider passiert das genau dann, wenn wir jeweils den
ersten Schlüssel als Pivot-Element wählen und die
zu sortierende Menge bereits sortiert vorliegt.
|
 | Das Problem kann entschärft werden, wenn
mehr Aufwand in die Auswahl des Pivot-Elements
investiert wird (zufällige Auswahl beispielsweise
oder Median von drei ausgewählten Schlüsseln).
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Einige Zitate aus dem Buch von Glenford Myers, ``The Art of Software Testing'':
 | ``Testing is the process of executing a program with the
intent of finding errors.''
|
 | ``A good test case is one that has a high probability of
detecting an as-yet undiscovered error.''
|
 | ``A successful test case is one that finds an error.
An unsuccessful test case is one that causes a program
to produce the correct result.''
|
 | ``One should start with the assumption that the program
contains errors and then test the program to find as many
of the errors as possible.''
|
Erste Schlußfolgerungen:
 | Testen ist ein destruktiver Prozeß.
|
 | Der Aufwand, der in die Entwicklung von Tests
fließt, zahlt sich aus, wenn genügend Fehler
gefunden werden, deren Behebung später sehr
viel teuer kommen würden (z.B. nach Auslieferung
eines Software-Produkts).
|
 | Tests erlauben es, die Existenz von Fehlern
nachzuweisen, jedoch nicht die Korrektheit eines
Programms.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Zitiert aus dem Werk von Glenford Myers, ``The Art of Software Testing'':
 | A necessary part of a test case is a definition of
the expected output or result.
|
 | A programmer should avoid attempting to test his or own
program.
|
 | A programming organization should not test its own
programs.
|
 | Thoroughly inspect the results of each test.
|
 | Test cases must be written for invalid and unexpected,
as well as valid and expected, input conditions.
|
 | Examining a program to see if it does not do what it
is supposed to do is only half of the battle. The other
half is seeing whether the program does what it is not
supposed to do.
|
 | Avoid throw-away test cases unless the program is
truly a throw-away program.
|
 | Do not plan a testing effort under the tacit assumption
that no errors will be found.
|
 | The probability of the existence of more errors in a
section of a program is proportional to the number of errors
already found in that section.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgende Begriffe wurden zuerst von Flaviu Cristian 1985 formal definiert (in einer Arbeit über die Robustheit von Software) und später von anderen übernommen. Hier sind einige informelle Definitionen:
 | Versagen (failure):
Ein Programm verhält sich abweichend von der Spezifikation.
|
 | Fehler (error): Der interne Zustand eines laufenden
Programms ist unzulässig oder inkonsistent. Beispiele:
Undefinierte Variablen, die hätten initialisiert werden müssen,
Verletzungen von Invarianten, Vor- oder Nachbedingungen.
|
 | Mangel (fault): Fehlerhafter Programmtext, der
zum Auftreten von Fehlern während der Laufzeit führen kann.
|
Mängel sind statische Bestandteile des Programmtexts, die während eines Programmlaufs zu Fehlern führen können. Interne Fehler können wiederum zu einem von außen sichtbaren Versagen des Programms führen (Black-Box-Perspektive).
Testfälle dienen dazu, das Versagen eines Programms festzustellen. Während der Fehler-Analyse (Debugging) wird nach fehlerhaften Zuständen gesucht, die dann auf Mängel zurückgeführt werden, die dann letztenendes behoben werden können.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Einzelne Programmteile können einem
Test unterworfen werden, z.B. Module, Klassen
oder einzelne Prozeduren.
Vorteil: Tests können frühzeitig entwickelt und zum Einsatz gebracht werden, lange bevor das gesamte Programm fertig wird. Das Finden der Mängel wird ebenfalls vereinfacht, weil die zu testenden Programmteile überschaubarer sind.
|
 | Testen höheren Grades, d.h. ein vollständiges
Programm wird getestet.
Selbst sehr gründliche Tests aller Programmteile können nicht sicherstellen, daß das Gesamtwerk frei von Mängeln ist, da es häufig zu Inkonsistenzen zwischen den einzelnen Programmteilen kommt.
Ferner können auf dieser Ebene Durchsatztests,
Stress-Tests und Sicherheits-Tests durchgeführt werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Black-Box-Test: Der Tester betrachtet das Programm
(oder den zu testenden Programmteil) als ``black box'',
dessen Internals unbekannt sind. Entsprechend werden
die Tests nur aus der Spezifikation abgeleitet ohne
Kenntnisse der Implementierung.
|
 | White-Box-Test: Testfälle werden von der internen
Struktur des zu testenden Programms (oder Programmteils)
und der Spezifikation abgeleitet. Diese Strategie geht
davon aus, daß die Mängel in einzelnen Ausdrücken,
Anweisungen oder Bedingungen stecken. Entsprechend werden
Testfälle entwickelt mit dem Ziel, alle Anweisungen,
Verzweigungen, Bedingungen und/oder Pfade abzudecken.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Black-Box:
| ||||||||
 | White-Box:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Folgendes Beispiel wurde dem Werk ``The Art of Software Testing'' von Glenford Myers entnommen:
Spezifikation:
Drei ganzzahlige Zahlen sind von dem Programm von der Standard-Eingabe zu lesen. Diese Zahlen sind als Längen der drei Seiten eines Dreiecks zu interpretieren. Das Programm hat auszugeben, ob das Dreieck gleichseitig (equilateral), gleichschenklig (isosceles) oder ungleichmäßig (scalene) ist.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Definitionen für die Tabelle auf der folgenden Seite:
 | Sei a die erste ganze Zahl, b die zweite und
c die dritte.
|
 | W steht fuer ``ganze Zahl''.
|
 | tr ist eine Kurzform für
(a + b > c) AND (a + c > b) AND
(b + c > a),
d.h. die Summe zwei beliebiger Seiten ist länger als
die dritte Seite.
|
 | maxint sei die größte ganze Zahl, die von der
lokalen Implementierung repräsentiert werden kann.
|
 | NUMBER steht für eine beliebige Zahl, wobei es
sich um eine ganze Zahl oder um eine Gleitkommazahl
handeln kann.
|
a, b, c W AND > 0 ist so zu interpretieren:
``a und b und c sind ganze Zahlen und größer als 0.''
a, b, c NOT W ist so zu interpretieren:
``Nicht (a und b und c sind ganze Zahlen)'', d.h. ``a oder
b oder c ist keine ganze Zahl.''
Diese Definitionen und die folgende Aufteilung in Äquivalenz-Klassen wurde aus einem Skript von Franz Schweiggert, Universität Ulm, entnommen.
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Klasse | Beschreibung | Erwartete Ausgabe |
| 1 | a, b, c W AND > 0 AND tr AND | |
| (a ≠ b ≠ c) AND <= maxint | scalene | |
| 2 | a, b, c W AND > 0 AND tr AND | |
| (a = b = c) AND <= maxint | equilateral | |
| 3 | a, b, c W AND > 0 AND tr AND | |
| NOT (a ≠ b ≠ c) AND | ||
| NOT (a = b = c) AND | ||
| <= maxint | isosceles | |
| 4 | a, b, c W AND > 0 AND | |
| NOT tr AND <= maxint | no triangle | |
| 5 | a, b, c W AND > 0 AND tr AND | |
| NOT <= maxint | invalid input | |
| 6 | a, b, c W AND NOT > 0 | non-positive length(s) |
| 7 | a, b, c NOT W AND > 0 AND tr | invalid input |
| 8 | a, b, c NOT NUMBER | invalid input |
 | In diesem Beispiel hängt die erwartete Ausgabe
nur von der Äquivalenzklasse ab. Dies ist natürlich
nicht zutreffend im allgemeinen Falle, bei dem für
jeden Testfall einzeln die zu erwartende Ausgabe
anzugeben ist.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Klasse | Nummer | Eingabedaten |
| 1 | 1 | 3, 4, 5 |
| 2 | maxint-2, maxint-1, maxint | |
| 2 | 3 | 3, 3, 3 |
| 4 | maxint, maxint, maxint | |
| 3 | 5 | 3, 3, 4 |
| 6 | 3, 4, 3 | |
| 7 | 4, 3, 3 | |
| 8 | maxint-1, maxint-1, maxint | |
| 9 | maxint-1, maxint, maxint-1 | |
| 10 | maxint, maxint-1, maxint-1 | |
| 4 | 11 | 1, 2, 3 |
| 12 | 3, 1, 2 | |
| 13 | 1, 3, 2 | |
| 14 | 1, 2, 4 | |
| 15 | 1, 4, 2 | |
| 16 | 4, 1, 2 | |
| 17 | maxint, 1, 1 | |
| 5 | 18 | maxint, maxint+1, maxint |
| 6 | 19 | 0, 0, 0 |
| 20 | -2, 2, 2 | |
| 21 | 2, -2, -2 | |
| 22 | -2, -2, -2 | |
| 7 | 23 | 3.14, 3.14, 3.14 |
| 8 | 24 | #, a, ? |
| 25 | 3, &, _ | |
 | Hinweis: Die zu erwartende Ausgabe ist
bei diesem Beispiel bereits bei den Äquivalenzklassen
angegeben worden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE Triangles;
IMPORT Read, Streams, Write;
(* ... *)
PROCEDURE DoIt;
VAR
len1, len2, len3: INTEGER;
BEGIN
IF ~ReadIntegers(len1, len2, len3) THEN
Write.Line("invalid input");
ELSIF (len1 <= 0) OR (len2 <= 0) OR (len3 <= 0) THEN
Write.Line("non-positive length(s)");
ELSIF ~IsTriangle(len1, len2, len3) THEN
Write.Line("no triangle");
ELSIF IsEquilateral(len1, len2, len3) THEN
Write.Line("equilateral");
ELSIF IsIsosceles(len1, len2, len3) THEN
Write.Line("isosceles");
ELSE
Write.Line("scalene");
END;
END DoIt;
BEGIN
DoIt;
END Triangles.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE IsTriangle(len1, len2, len3: INTEGER) : BOOLEAN; BEGIN RETURN (len1 + len2 > len3) & (len1 + len3 > len2) & (len2 + len3 > len1) END IsTriangle; PROCEDURE IsEquilateral(len1, len2, len3: INTEGER) : BOOLEAN; BEGIN RETURN (len1 > 0) & (len1 = len2) & (len2 = len3) END IsEquilateral; PROCEDURE IsIsosceles(len1, len2, len3: INTEGER) : BOOLEAN; BEGIN RETURN IsTriangle(len1, len2, len3) & ((len1 = len2) OR (len1 = len3) OR (len2 = len3)) END IsIsosceles; PROCEDURE ReadIntegers(VAR len1, len2, len3: INTEGER) : BOOLEAN; PROCEDURE ReadInteger(VAR intval: INTEGER) : BOOLEAN; BEGIN Read.Int(intval); RETURN Streams.stdin.count > 0 END ReadInteger; BEGIN (* ReadIntegers *) RETURN ReadInteger(len1) & ReadInteger(len2) & ReadInteger(len3) END ReadIntegers; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
3 4 5:scalene 2147483645 2147483646 2147483647:scalene 3 3 3:equilateral 2147483647 2147483647 2147483647:equilateral 3 3 4:isosceles 3 4 3:isosceles 4 3 3:isosceles 2147483646 2147483646 2147483647:isosceles 2147483646 2147483647 2147483646:isosceles 2147483647 2147483646 2147483646:isosceles 1 2 3:no triangle 3 1 2:no triangle 1 3 2:no triangle 1 2 4:no triangle 1 4 2:no triangle 4 1 2:no triangle 2147483647 1 1:no triangle 2147483647 2147483648 2147483647:invalid input 0 0 0:non-positive length(s) -2 2 2:non-positive length(s) 2 -2 -2:non-positive length(s) -2 -2 -2:non-positive length(s) 3.14 3.14 3.14:invalid input # a ?:invalid input 3 & _:invalid input |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
3 4 5:scalene 2147483645 2147483646 2147483647:scalene 3 3 3:equilateral 2147483647 2147483647 2147483647:equilateral |
 | Es sollte möglichst leicht sein, Testfälle
hinzuzufügen oder zu verändern.
|
 | In diesem Beispiel stehen alle Testfälle in
einer Datei.
|
 | Jede nicht-leere Zeile enthält die Standard-Eingabe,
einen Doppelpunkt als Feldtrenner und die erwartete Ausgabe.
|
 | Solche Eingabe-Formate können leicht erweitert werden,
um komplexeren Anforderungen zu genügen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
MODULE TriangleTester; IMPORT Read, Sets, StreamDisciplines, Streams, UnixFiles, UnixPipes, Write; CONST maxlen = 128; TYPE TestCase = RECORD input: ARRAY maxlen OF CHAR; expected: ARRAY maxlen OF CHAR; output: ARRAY maxlen OF CHAR; END; (* ... *) BEGIN RunTestCases; END TriangleTester. |
 | Ein Testfall besteht aus der Eingabe und der
zu erwartenden Ausgabe. Sobald ein Test durchgeführt
worden ist, kommt dann noch das beobachtete Resultat
hinzu.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE RunTestCases;
VAR
tests: Streams.Stream;
test: TestCase;
noftests, failures: INTEGER;
BEGIN
IF ~OpenTestCases(tests) THEN
Write.Line("Unable to open file with test cases!");
RETURN
END;
noftests := 0; failures := 0;
WHILE ReadTestCase(tests, test) DO
INC(noftests);
IF ~RunTestCase(test) THEN
INC(failures);
LogTestCase(noftests, test);
END;
END;
Write.Int(failures, 1); Write.Char("/");
Write.Int(noftests, 1); Write.Line(" tests failed.");
END RunTestCases;
|
 | Für jeden eingelesenen Testfall wird der
Test durchgeführt und bei einem Versagen des
Testkandidats wird ein Testprotokoll ausgegeben.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE OpenTestCases(VAR in: Streams.Stream) : BOOLEAN; CONST filename = "triangle.tests"; fieldsep = ":"; VAR fieldseps: Sets.CharSet; BEGIN IF ~UnixFiles.Open(in, filename, UnixFiles.read, Streams.onebuf, NIL) THEN RETURN FALSE END; Sets.InitSet(fieldseps); Sets.InclChar(fieldseps, fieldsep); StreamDisciplines.SetFieldSepSet(in, fieldseps); RETURN TRUE END OpenTestCases; PROCEDURE ReadTestCase(in: Streams.Stream; VAR test: TestCase) : BOOLEAN; BEGIN LOOP test.output := ""; IF Read.FieldS(in, test.input) & Read.FieldS(in, test.expected) THEN Read.LnS(in); RETURN in.count > 0 END; IF in.eof OR in.error THEN RETURN FALSE END; (* skip an empty line *) Read.LnS(in); END; END ReadTestCase; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE RunTestCase(VAR test: TestCase) : BOOLEAN;
VAR
stdin, stdout, stderr: Streams.Stream;
BEGIN
IF ~UnixPipes.Spawn3("./Triangles", Streams.linebuf,
stdin, stdout, stderr, NIL) THEN
RETURN FALSE
END;
Write.LineS(stdin, test.input); Streams.Release(stdin);
Read.LineS(stdout, test.output); Streams.Release(stdout);
Streams.Release(stderr);
RETURN test.output = test.expected
END RunTestCase;
|
 | Mit UnixPipes.Spawn3 wird ein Programm so
gestartet, daß die Standard-Eingabe, Standard-Ausgabe
und die Standard-Fehlerausgabe des neuen Prozesses
mit dem aufrufenden Prozess verbunden sind.
|
 | Pipes sind unter UNIX unidirektionale Kommunikationskanäle
zwischen Prozessen.
|
 | Auf der Kommandozeile werden sie mit einem senkrechten Strich
konstruiert. Beispiel: ls /usr/bin | grep cal |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE RunTestCase(VAR test: TestCase) : BOOLEAN;
VAR
stdin, stdout, stderr: Streams.Stream;
BEGIN
IF ~UnixPipes.Spawn3("./Triangles", Streams.linebuf,
stdin, stdout, stderr, NIL) THEN
RETURN FALSE
END;
Write.LineS(stdin, test.input); Streams.Release(stdin);
Read.LineS(stdout, test.output); Streams.Release(stdout);
Streams.Release(stderr);
RETURN test.output = test.expected
END RunTestCase;
|
 | Zu beachten ist hier, daß die Bezeichnungen
stdin, stdout und stderr aus der
Sicht des aufgerufenen Programms so benannt sind.
|
 | Entsprechend wird bei der Prozedur RunTestCase
auf stdin geschrieben und diese Ausgabe erscheint
dann als Eingabe beim aufgerufenen Programm.
|
 | Die Ausgabe von Triangles kann dann danach
von stdout gelesen werden.
|
 | Die Fehlerausgabe stderr wird hier nicht
weiter ausgewertet.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
dublin$ ./TriangleTester 2: input = '2147483645 2147483646 2147483647' expected = 'scalene' output = 'no triangle' 4: input = '2147483647 2147483647 2147483647' expected = 'equilateral' output = 'no triangle' 8: input = '2147483646 2147483646 2147483647' expected = 'isosceles' output = 'no triangle' 9: input = '2147483646 2147483647 2147483646' expected = 'isosceles' output = 'no triangle' 10: input = '2147483647 2147483646 2147483646' expected = 'isosceles' output = 'no triangle' 5/25 tests failed. dublin$ |
 | Beim Testen stellt sich hier heraus, daß keine
Vorkehrungen für mögliche Überläufe beim Addieren
getroffen worden sind:
|
PROCEDURE IsTriangle(len1, len2, len3: INTEGER) : BOOLEAN; BEGIN RETURN (len1 + len2 > len3) & (len1 + len3 > len2) & (len2 + len3 > len1) END IsTriangle; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE IsTriangle(len1, len2, len3: INTEGER) : BOOLEAN; BEGIN RETURN (len1 > len3 - len2) & (len1 > len2 - len3) & (len2 > len1 - len3) END IsTriangle; |
 | Die Problematik mit den Überläufen läßt sich
durch die Betrachtung von Differenzen vermeiden.
|
dublin$ ./TriangleTester 0/25 tests failed. dublin$ |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | Bei der traditionellen Entwicklungsmethodik
(Spezifikation, Entwurf, Implementierung, Testen,
Wartung) wird erst sehr spät getestet und das Testen
kann daher leicht zum Opfer des Termindrucks werden.
|
 | Bei dem Ansatz ``Test First'' der Entwicklungsmethodik
des ``Extreme Programming'' werden zuerst die Testfälle
und die Testwerkzeuge entwickelt. Dann wird soweit
die Implementierung vorangetrieben, daß genau
die bislang entwickelten Testfälle erfolgreich
bestanden werden. Danach werden weitere Testfälle
entwickelt und entsprechend wird die Implementierung
umfassender.
|
 | Beim ``Cleanroom Development'' von Harlan Mills
wird das Entwickeln der Implementierung und der Testfälle
vollständig getrennt. Die Entwickler der Implementierung
dürfen selbst ihr Werk nicht testen oder ausführen, sondern
müssen fertige Programmteile an die Tester übergeben, die
mit statischen Qualitätskontrollen arbeiten. Mangelbehaftete
Programmteile werden dann intensiveren Kontrollen unterzogen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
 | White-Box-Tests gehen davon aus, daß viele
Mängel in einzelnen Anweisungen, Ausdrücken oder
der Logik von Bedingungen versteckt sind.
| ||||||||
 | Um möglichst viele dieser Mängel zu
entdecken, wird nach Testfällen gesucht, die
eine möglichst große Menge von denkbaren Pfaden
durch das Programm abdecken.
| ||||||||
 | Leider führt eine vollständige Abdeckung
zu einer astronomisch hohen Zahl von Testfällen.
| ||||||||
 | Folgende Abdeckungen sind üblich:
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
Sei folgende Spezifikation gegeben für einen Programmtext-Abschnitt, der Teil eines Bisektions-Algorithmus sein könnte, der Näherungen für
|
 | Eingabe-Parameter sind die Gleitkommazahlen a und b.
|
 | Vertausche a und b, es sei denn a <= b.
|
 | Setze a und b zu den Werten 1 und 3,
es sei denn cos(a) >= 0 und cos(b) <= 0.
|
 | Setze x zum arithmetischen Mittel aus a und b.
|
 | Setze a zu x, falls cos(x) > 0 und
b zu x andernfalls.
|
 | Gebe a und b aus.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
PROCEDURE NextStep(VAR a, b: REAL); VAR x, tmp: REAL; BEGIN IF a > b THEN tmp := b; b := a; a := tmp; END; IF (Math.Cos(a) < 0) & (Math.Cos(b) > 0) THEN a := 1; b := 3; END; x := (a + b) / 2; IF Math.Cos(x) > 0 THEN a := x; ELSE b := x; END; END NextStep; |
 | Diese Implementierung enthält einen Mangel: In
der zweiten IF-Anweisung wird & anstelle
von OR verwendet.
| ||||||||||||||||
 | Um die Abdeckung der folgenden Testfälle zu
analysieren, werden folgende Abkürzungen verwendet:
| ||||||||||||||||
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Abdeckung | Eingabe | Abdeckung | Erwartet | Beobachtet |
| C0: | 5,2 | ACF (TT) | 1,2 | 1,2 |
| 8,6 | ADE (FF) | 7,8 | 7,8 | |
| C1: | 2,5 | BCF (TT) | 1,2 | 1,2 |
| C2: | 4,4 | BDF (TF) | 4,4 | 1,2 |
| 7,5 | ADE (FT) | 6,7 | 1,2 | |
| C7: | 4,8 | BDE (TF) | 6,8 | 1,2 |
| 9,7 | ADF (FF) | 7,8 | 7,8 | |
 | (TT), (FF), (FT) und (TF) spezifizieren die BOOLEAN-Werte
der beiden Teilbedingungen in der mangelhaften zweiten
IF-Anweisung.
|
 | C0 versucht, alle Anweisungen abzudecken. Dabei werden
nicht die leeren ELSE-Fälle berücksicht, d.h.
B fällt hier weg.
|
 | C1 fügt einen Testfall für B hinzu.
|
 | C2 vervollständigt die Menge der möglichen BOOLEAN-Werte
(soweit kamen nur (TT) und (FF) vor).
|
 | C7 fügt BDE und ADF hinzu, die noch in der Menge der
insgesamt sechs möglichen Pfade fehlten. Zu beachten ist
hier, daß ACE und BCE unmöglich sind, da E nicht mehr
erreicht werden kann, wenn C erreicht wurde.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
![[Nächstes Kapitel]](nnext.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
| Beispiel herunterladen |
 | Plex-Skript |
 | FTP-Verzeichnis |
 | HTML-Verzeichnis |
| Zugehörige Seiten im Skript |
 | Ein Test-Kandidat |
 | Ein Test-Kandidat II |
 | Ein Testwerkzeug |
 | Ein Testwerkzeug II |
 | Ein Testwerkzeug III |
 | Ein Testwerkzeug IV |
 | Ein Testwerkzeug V |
 | Ein Testlauf |
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
 | Prozeduraufrufe werden mit Hilfe eines Stapels
realisiert. Ganz oben auf dem Stapel sind die Parameter und
lokalen Variablen der gerade aktiven Prozedur. Weiter unten im
Stapel sind die Parameter und lokalen Variablen der aufrufenden
Prozedur und die Rücksprungposition, an der das Programm
fortgesetzt wird, wenn die aktuelle Prozedur beendet wird.
|
 | Normalerweise wird nur ein Stapel verwendet.
|
 | Wenn mehrere solcher Stapel gleichzeitig existieren
können, wird von Koroutinen gesprochen.
|
 | Jede Koroutine hat somit ihren eigenen Kontrollfluß
durch das Programm.
|
 | Zu jedem Zeitpunkt ist aber nur eine Koroutine aktiv.
|
 | Es ist möglich, neue Koroutinen zu erzeugen und
von einer Koroutine zu einer anderen zu wechseln.
|
 | Der Vorteil von Koroutinen liegt darin, daß sich damit
ineinander verzahnte Algorithmen trennen lassen, die sonst
ineinander verwoben wären.
|
 | Umgekehrt können Koroutinen auch sehr zur Unübersichtlichkeit
beitragen. Dies wird normalerweise vermieden, indem
die trickreichen Techniken hinter übersichtlichen
Bibliotheksschnittstellen versteckt werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
 | Für Koroutinen gibt es den Datentyp Coroutines.Coroutine.
Diese Datenstruktur besteht aus einem Stapel und die Position
der nächsten auszuführenden Instruktion.
|
 | Das Modul Coroutines stellt ferner die Variablen
Coroutines.current und Coroutines.source
zur Verfügung, die auf die derzeit aktive Koroutine und die
davor aktive Koroutine verweisen.
|
 | Im Modul SYSTEM gibt es die Operationen CRSPAWN
und CRSWITCH.
|
 | PROCEDURE CRSPAWN(VAR cr: Coroutines.Coroutine); erzeugt eine neue Koroutine, wobei der neue Koroutinen-Stapel zunächst nur aus den Parametern und lokalen Variablen der aufrufenden Prozedur besteht. Die nächste Instruktion der neuen Koroutine liegt unmittelbar hinter der CRSPAWN-Anweisung. Die alte (aufrufende) Koroutine beendet sofort die Ausführung der Prozedur, als ob RETURN aufgerufen worden wäre. |
 | Prozeduren, die sich zu neuen Koroutinen machen, müssen
globale Prozeduren sein und dürfen keinen Rückgabewert haben.
Ein RETURN der Koroutinen-Prozedur ist nach CRSPAWN
nicht mehr zulässig, da es dafür keine Rückkehrposition mehr
gibt.
|
 | PROCEDURE CRSWITCH(cr: Coroutines.Coroutine); wechselt zu der angegebenen Koroutine. Die aufrufende Koroutine steht nach dem Wechsel unter Coroutines.source zur Verfügung. |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
MODULE HaTschi; IMPORT Coroutines, Random := RandomGenerators, SYS := SYSTEM, Write; PROCEDURE Ha(VAR ha, tschi: Coroutines.Coroutine); (* ... *) PROCEDURE Tschi(VAR ha, tschi: Coroutines.Coroutine); (* ... *) PROCEDURE DoIt; VAR ha, tschi: Coroutines.Coroutine; BEGIN Ha(ha, tschi); Tschi(ha, tschi); SYS.CRSWITCH(ha); END DoIt; BEGIN DoIt; END HaTschi. |
 | In diesem Beispiel sind drei Koroutinen aktiv:
Zunächst die Koroutine, die zu Beginn loslegt (Haupt-Koroutine).
Dann wird je von den Prozeduren Ha und Tschi
eine Koroutine neu erzeugt.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE Ha(VAR ha, tschi: Coroutines.Coroutine);
BEGIN
SYS.CRSPAWN(ha);
LOOP
REPEAT
Write.String("Ha");
UNTIL Random.Val(1, 5) = 1;
SYS.CRSWITCH(tschi);
END;
END Ha;
|
 | Gleich zu Beginn des Aufrufes erzeugt die Prozedur Ha
eine neue Koroutine. Über den Referenz-Parameter ha
erhält der Aufrufer einen Verweis auf die neu geschaffene
Koroutine.
|
 | Der Referenz-Parameter tschi hat zunächst einen
undefinierten Wert. Aber sobald die so referenzierte
Variable beim Erzeugen der nächsten Koroutine durch Tschi
einen Wert erhält, wird er hier zugänglich.
|
 | Erst mit dem Aufruf SYS.CRSWITCH(ha); findet der
erste Wechsel von der Haupt-Koroutine zur Koroutine ha statt.
Diese beginnt dann ihre Ausführung ab dem LOOP, also
unmittelbar hinter SYS.CRSPAWN.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE Tschi(VAR ha, tschi: Coroutines.Coroutine);
VAR
main: Coroutines.Coroutine;
i: INTEGER;
BEGIN
main := Coroutines.current;
SYS.CRSPAWN(tschi);
i := 0;
WHILE i < 10 DO
Write.Line("Tschi!");
SYS.CRSWITCH(ha);
INC(i);
END;
SYS.CRSWITCH(main);
END Tschi;
|
 | Die Prozedur Tschi notiert sich zunächst
einen Verweis auf die aktuelle Koroutine, wenn sie
aufgerufen wird. Das erlaubt später die Rückkehr
zur Haupt-Koroutine, sobald die beiden Koroutinen
ihr Wechselspiel beendet haben.
|
 | Danach wird mit SYS.CRSPAWN(tschi); die neue
Koroutine erzeugt, die dann später erst aktiviert
wird, wenn die Koroutine ha zum ersten Mal
nach tschi wechselt.
|
 | Nach 10 Wechseln endet das Spiel mit SYS.CRSWITCH(main);.
Dann geht es bei der Hauptkoroutine unmittelbar hinter
dem SYS.CRSWITCH(ha); in der Prozedur DoIt weiter.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
 | Die Koroutinen-Operationen CRSPAWN und CRSWITCH
können nicht weiter vereinfacht werden.
| ||||
 | Alle lästigen Arbeiten werden im ``Hintergrund'' erledigt.
So wird vollautomatisch der Speicherbereich für den Stapel
organisiert. Ferner können die Stapel (soweit genügend
Speicherplatz zur Verfügung steht) beliebig wachsen. Und
zu guter Letzt werden nicht mehr erreichbare Koroutinen
automatisch entsorgt.
| ||||
 | Dennoch sind Koroutinen bei direkter Verwendung
sehr unübersichtlich, da
| ||||
 | Glücklicherweise gibt es freundlichere Schnittstellen,
die auf Basis der Koroutinen-Operationen eingerichtet werden
können und bei denen die Nachteile wegfallen.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
TYPE Filter = PROCEDURE (in, out: Streams.Stream); PROCEDURE Open(VAR out, in: Streams.Stream; bufmode: Streams.BufMode); PROCEDURE Spawn(filter: Filter; in, out: Streams.Stream); |
 | Das Modul CrPipes ermöglicht es, auf Basis
von Koroutinen und Filtern interne Pipelines zu bauen.
|
 | Ein Filter ist dabei eine Prozedur, die von einer
Eingabe-Verbindung liest und die Eingabe nach Modifikationen
wieder ausgibt.
|
 | So sieht beispielsweise ein Filter aus, der sämtliche
Kleinbuchstaben in Großbuchstaben verwandelt:
|
PROCEDURE UpperCase(in, out: Streams.Stream); VAR ch: CHAR; BEGIN WHILE Streams.ReadByte(in, ch) DO IF (ch >= "a") & (ch <= "z") THEN ch := CAP(ch); END; IF ~Streams.WriteByte(out, ch) THEN RETURN END; END; END UpperCase; |
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE InstallInputFilter(filter: CrPipes.Filter); VAR out, in: Streams.Stream; BEGIN CrPipes.Open(out, in, Streams.onebuf); CrPipes.Spawn(filter, Streams.stdin, out); Streams.stdin := in; END InstallInputFilter; |
 | Mit CrPipes.Open wird eine neue Pipeline
erzeugt. Ausgaben, die auf out erfolgen, können danach
von in gelesen werden. Allerdings funktioniert dies
hier nur dann, wenn der Schreiber und der Leser verschiedene
Koroutinen sind.
|
 | Mit CrPipes.Spawn wird eine neue Koroutine
erzeugt, die später den angegebenen Filter verwenden wird.
Hier wird der Filter von Streams.stdin lesen und in
das schreibende Ende der zuvor erzeugten Pipeline schreiben.
|
 | Danach wird Streams.stdin auf das lesende Ende
der Pipeline gesetzt. Damit werden alle Eingaben von
Streams.stdin implizit gefiltert.
|
 | Bei der Verwendung von CrPipes sind keine
Koroutinen-Operationen mehr zu sehen und die
Filter-Prozeduren können auch ganz normal enden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
MODULE Filters; IMPORT Args := UnixArguments, CrPipes, Read, Streams, Write; PROCEDURE UpperCase(in, out: Streams.Stream); (* ... *) PROCEDURE RemoveEmptyLines(in, out: Streams.Stream); (* ... *) PROCEDURE ProcessArgs; (* ... *) PROCEDURE DoIt; VAR ok: BOOLEAN; BEGIN ok := Streams.Copy(Streams.stdin, Streams.stdout, -1); END DoIt; BEGIN ProcessArgs; DoIt; END Filters. |
 | ProcessArgs hat hier die Möglichkeit,
beliebig viele Filter vor Streams.stdin einzufügen.
|
 | Die Prozedur Doit, die hier die Verarbeitung
übernimmt, bleibt hier völlig unabhängig von der
Filterung der Eingabe.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE ProcessArgs;
VAR
flag: CHAR;
PROCEDURE InstallInputFilter(filter: CrPipes.Filter);
(* ... *)
BEGIN (* ProcessArgs *)
Args.Init("[-e] [-u]");
WHILE Args.GetFlag(flag) DO
CASE flag OF
| "e": InstallInputFilter(RemoveEmptyLines);
| "u": InstallInputFilter(UpperCase);
ELSE
Args.Usage
END;
END;
Args.AllArgs;
END ProcessArgs;
|
 | Dabei können beliebig viele Filter hintereinander
installiert werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
 | Bei verschiedenen Programmen (z.B. der bash) ist
es möglich, frühere Eingaben wiederzuverwenden.
|
 | Dies läßt sich auch über interne Filter auf
Basis von CrPipes implementieren und hat dabei wieder
den Vorteil, daß dieser Mechanismus sich völlig unabhängig
von der späteren Verarbeitung programmieren läßt.
|
 | Hier zahlen sich Koroutinen wirklich aus, da
der Filter einen nicht-trivialen Status verwaltet.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
 | Beim Übungsblatt 13 von Norbert Heidenbluth
wurde ein Programm entwickelt, mit dem eine virtuelle Wanderung
durchgeführt werden konnte.
| ||||
 | Hier wäre es sinnvoll, wenn bereits zuvor eingegebene
Pfade erneut abgespielt werden könnten.
| ||||
 | Eingabesyntax:
Alle anderen Eingabe-Zeilen sollen unverändert
weitergegeben werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
CONST
letters = ORD("z") - ORD("a") + 1;
VAR
marks: ARRAY letters OF Streams.Count;
history: Streams.Stream;
line: ARRAY 512 OF CHAR;
|
 | Alle Eingaben müssen bewahrt werden, damit sie später
wieder eingefügt werden können.
|
 | Dies geschieht über eine interne Datei aus dem
Modul Texts. Auf diese wird über die Variable
history zugegriffen, die vom Typ Streams.Stream
ist.
|
 | Das Array marks notiert die markierten Positionen,
die sich alle auf history beziehen. Bei einer
Eingabe von !a ist marks[0] auf die aktuelle Position
von history zu setzen.
|
 | Die Variable line dient als Puffer für die
aktuelle Zeile.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE Init; VAR i: INTEGER; BEGIN i := 0; WHILE i < letters DO marks[i] := -1; INC(i); END; END Init; |
 | Zu Beginn werden alle denkbaren Markierungen mit -1
vor initialisiert.
|
 | Sie werden erst benutzbar, wenn Sie mit einer
(nicht-negativen) Position belegt werden.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE HistoryFilter(in, out: Streams.Stream); (* ... *) PROCEDURE ProcessCommand; (* ... *) BEGIN (* HistoryFilter *) Init; Texts.Open(history); LOOP Read.LineS(in, line); IF in.count = 0 THEN EXIT END; IF (line[0] # "!") THEN Write.LineS(history, line); Write.LineS(out, line); ELSE ProcessCommand; END; END; END HistoryFilter; |
 | Mit Texts.Open wird eine interne Datei zum
Lesen und Schreiben eröffnet.
|
 | Danach wird zeilenweise gelesen. Zeilen, die
mit einem Ausrufe-Zeichen beginnen werden der
Sonderbehandlung von ProcessCommand überlassen.
Alle anderen Zeilen werden unverändert durchgereicht.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
PROCEDURE ProcessCommand;
VAR
ch1, ch2: CHAR;
index1, index2: INTEGER;
currentPos: Streams.Count;
len: Streams.Count; ok: BOOLEAN;
(* ... *)
BEGIN (* ProcessCommand *)
Streams.GetPos(history, currentPos);
ch1 := line[1]; ch2 := line[2];
IF (ch1 >= "a") & (ch1 <= "z") THEN
index1 := ORD(ch1) - ORD("a");
IF ch2 = 0X THEN
marks[index1] := currentPos;
ELSIF (ch2 >= "a") & (ch2 <= "z") THEN
index2 := ORD(ch2) - ORD("a");
IF (marks[index1] >= 0) &
(marks[index2] > marks[index1]) THEN
len := marks[index2] - marks[index1];
Write.String("*** copying "); Write.Int(len, 1);
Write.Line(" bytes from history:");
Streams.SetPos(history, marks[index1]);
ok := Streams.Copy(history, out, len);
ASSERT(ok);
Write.Line("*** copying finished");
Streams.SetPos(history, currentPos);
ELSE
Write.Line("Invalid range!");
END;
ELSE Help;
END;
ELSE Help;
END;
END ProcessCommand;
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
![[Nächste Seite]](next.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
|
 | Koroutinen sind sinnvoll, wenn
| ||||||
 | Synchronisierung und Koroutinen-Verwaltung müssen
dabei in entsprechende Module ausgelagert werden,
da die direkte Verwendung zu unübersichtlich ist.
| ||||||
 | Die Ulmer Oberon-Bibliothek bietet verallgemeinerte
Synchronisierungsmechanismen und Verwaltungen an
über die Module Conditions, Tasks und
Jobs.
| ||||||
 | Alternativen zu Koroutinen sind Continuations
(Scheme) und Threads (parallel laufende Kontrollflüsse
im gleichen Adreßraum). Continuations sind jedoch
schwerer zu implementieren und Threads bringen ein
hohes Fehlerrisiko mit sich.
|
![[Vorheriges Kapitel]](pprev.gif)
![[Vorherige Seite]](prev.gif)
![[Inhaltsverzeichnis]](up.gif)
|
| Copyright © 2004, 2005 Andreas Borchert, in HTML konvertiert am 18.02.2005 |