It is often necessary to simulate the typical clump of a Boolean model, e.g.
for testing hypotheses where the exact distribution of the test statistic
is unknown. But Monte Carlo simulation can be used in order to obtain
an approximative empirical reference distribution; see Hermann et al.
(1989), Hinde and Miles (1980),
Møller (1994). In connection with this
a simulation procedure is useful which has been
developed in Møller (1994) and which is based
on an algorithm due to Quine and Watson (1984) for
radial simulation of a homogeneous Poisson process.
Let ![]() be independent random vectors uniformly
distributed on the circle
be independent random vectors uniformly
distributed on the circle ![]() and let
and let
![]() be independent random variables uniformly distributed
on the interval (0,1). Furthermore, assume that the sequences
be independent random variables uniformly distributed
on the interval (0,1). Furthermore, assume that the sequences
![]() and
and ![]() are independent. For
are independent. For ![]() fixed,
we put
fixed,
we put
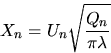 |
(25) |
This radial simulation procedure of the homogeneous
Poisson process X can be used for simulating the typical clump of the
Boolean model. As we already mentioned, we can simulate the clump which
contain the disc with center at the origin which is induced by the
point process ![]() , where a point at the origin has been
added to X. As before, we assume that the radii of the discs are
bounded by
, where a point at the origin has been
added to X. As before, we assume that the radii of the discs are
bounded by ![]() . By
. By ![]() we will denote
the clump induced by the discs centered at
we will denote
the clump induced by the discs centered at ![]() and containing the disc with center at the origin.
Let
and containing the disc with center at the origin.
Let ![]() be a realization
of the radially generated Poisson process X and let
be a realization
of the radially generated Poisson process X and let ![]() be a realization of the sequence of radii
be a realization of the sequence of radii ![]() .
Hall (1988) showed that the clump
.
Hall (1988) showed that the clump ![]() which contains the disc centered at the origin is finite with
probability 1 if
which contains the disc centered at the origin is finite with
probability 1 if ![]() is smaller than a critical value
is smaller than a critical value ![]() ;see Hall (1988) for estimated critical intensities for Boolean models
generated by fixed-radius discs.
Let ln denote the distance of the farthest point of the clump
;see Hall (1988) for estimated critical intensities for Boolean models
generated by fixed-radius discs.
Let ln denote the distance of the farthest point of the clump
![]() to the origin and let
to the origin and let
![]() .
Note that
.
Note that
![]() for all
for all ![]() where n0 is finite with probability 1
if
where n0 is finite with probability 1
if ![]() . Thus, generate the realizations
. Thus, generate the realizations
![]() of
of ![]() until
until ![]() .
.