- a)
- Bestimmen Sie den Stichprobenmittelwert.
- b)
- Bestimmen Sie die Stichprobenvarianz und die Standardabweichung der Stichprobe.
- a)
- Bestimmen Sie den Stichprobenmittelwert, den Stichprobenmedian sowie den Modus und die Spannnweite der Stichprobe.
- b)
- Bestimmen Sie die Stichprobenvarianz und den empirischen Variationskoeffizienten.
- (c)
- Es sei bekannt, dass in einer grösseren Niederlassung desselben Autohauses pro Monat im Mittel 17.6 Autos mit einer Standardabweichung von 6.5 verkauft werden. Vergleichen Sie die Streuung der Autoverkäufe in den beiden Autohäusern sowohl absolut als auch relativ zum mittleren Niveau der Autoverkäufe in den beiden Autohäusern.
Vergleichen Sie die Variabilität der beiden Aktien A und B.
- (a)
- Berechnen Sie die relativen Häufigkeiten der Ergebnisse.
- (b)
- Erstellen Sie ein Histogramm der relativen Häufigkeiten.
- (c)
- Zeichnen Sie die empirische Verteilungsfunktion.
| 71 | 73 | 97 | 54 | 69 | 82 | 86 | 53 | 96 | 78 |
| 82 | 67 | 91 | 75 | 80 | 100 | 66 | 84 | 53 | 65 |
| 42 | 76 | 34 | 59 | 71 | 52 | 84 | 89 | 61 | 59 |
Bestimmen Sie aus der Tabelle
- (a)
- den Stichprobenmittelwert und die Stichprobenvarianz,
- (b)
- den empirischen Variationskoeffizient,
- (c)
- die Fünfer-Charakteristik und die Siebener-Charakteristik.
| Punkte | 100-91 | 90-80 | 79-64 | 63-50 | 49-0 |
| Note | sehr gut | gut | befriedigend | ausreichend | ungenügend |
Betrachten Sie wieder die in Aufgabe 5 angegebenen Punktezahlen der Wiwi-Studenten und
- (a)
- berechnen Sie die absoluten und die relativen Häufigkeiten für jede der hier angegebenen Klassen.
- (b)
- Erstellen Sie mit Hilfe der Klasseneinteilung ein Histogramm für die relativen Häufigkeiten.
- (c)
- Erstellen Sie einen Plot der empirischen Verteilungsfunktion der Punktezahlen (siehe Aufgabe 5).
Hinweis: Beachten Sie bei der Erstellung des Histogramms, dass die Klassenbreiten nicht gleich sind.
| Discounter | A | B | C | D | E |
| 1992 | 50 | 25 | 10 | 15 | - |
| 2002 | 25 | 25 | 20 | 20 | 10 |
- (a)
- Zeichnen Sie jeweils für die Jahre 1992 und 2002 die Lorenzkurve der Marktkonzentration und berechnen Sie sowohl den Gini-Koeffizienten als auch den normierten Gini-Koeffizienten für beide Jahre. Interpretieren Sie Ihre Ergebnisse, insbesondere auch hinsichtlich der Veränderung der Marktkonzentration in den letzten 10 Jahre.
- (b)
- Der Herfindahl-Index H ist ein weiteres gebräuchliches
Konzentrationsmaß. Es seien alle Beobachtungswerte nichtnegativ und
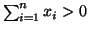 .
Dann ist
.
Dann ist
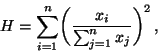
d.h.
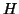 ergibt sich aus der Summe der Quadrate des
Merkmalsanteils der i-ten Einheit. Welchen Wertebereich besitzt
der Herfindahl-Index?
ergibt sich aus der Summe der Quadrate des
Merkmalsanteils der i-ten Einheit. Welchen Wertebereich besitzt
der Herfindahl-Index?
- (c)
- Berechnen Sie den Herfindahl-Index
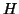 für das Jahr 2002
und vergleichen Sie ihn mit dem entsprechenden Gini-Koeffizienten.
für das Jahr 2002
und vergleichen Sie ihn mit dem entsprechenden Gini-Koeffizienten.
| Proband | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 120 | 119 | 122 | 120 | 121 | 119 | 115 | 122 | 117 | 123 | |
| 150 | 165 | 177 | 157 | 165 | 167 | 159 | 163 | 161 | 164 |
- (a)
- Erstellen Sie einen Scatterplot der Daten.
- (b)
- Berechnen Sie den empirischen Korrelationskoeffizienten und geben Sie eine Interpretation des Wertes.