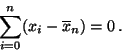
- (a)
- Bestimmen Sie die Punkte der Lorenzkurve und zeichnen Sie diese anschliessend. Berechnen Sie ausserdem den Gini-Koeffizienten (normiert und unnormiert).
- (b)
- Die grösste Facharztniederlassung konnte im folgenden Jahr (2002) ihr Einkommen nochmals um 50 Prozent steigern, während der Umsatz der übrigen Niederlassungen stagnierte. Wie ändern sich Lorenzkurve und Gini-Koeffizient?
- (c)
- Um der grossen Facharztniederlassung Paroli zu bieten, schliessen sich Anfang 2003 die 4 mittleren Praxen zu einer Praxisgemeinschaft zusammen. Bestimmen Sie nun wieder die Lorenzkurve und den Gini-Koeffizienten.
- (a)
- Zeigen Sie, dass für den
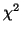 -Koeffizienten
-Koeffizienten 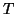 gilt
gilt
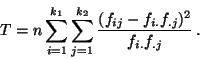
- (b)
- Wie ändert sich
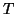 bei Verdopplung des Stichprobenumfangs (aber gleichbleibenden
relativen Häufigkeiten)?
bei Verdopplung des Stichprobenumfangs (aber gleichbleibenden
relativen Häufigkeiten)?
| Staatsangehörigkeit | ||
| Schulart | deutsch | ausländisch |
| Hauptschule | 173244 | 145917 |
| Realschule | 154255 | 7323 |
| Gymnasium | 290057 | 10043 |
Bestimmen Sie
- (a)
- die relativen Häufigkeiten von Schulart und Staatsangehörigkeit und die relativen Randhäufigkeiten der beiden Merkmale, sowie
- (b)
- die bedingten relativen Häufigkeiten der Schulart, gegeben die Staatsangehörigkeit.
- (c)
- Beschreiben Sie mit Hilfe der berechneten relativen Häufigkeiten, welcher Zusammenhang zwischen den beiden Merkmalen der Tendenz nach besteht, und
- (d)
- beurteilen Sie diesen Zusammenhang mit einem geeigneten statistischen Mass.
| Ja | Nein | Enthaltung | |
| Partei A | 85 | 78 | 37 |
| Partei B | 118 | 61 | 25 |
- (a)
- Bestimmen Sie die relativen Randhäufigkeiten.
- (b)
- Berechnen Sie den Kontingenzkoeffizienten und den korrigierten Kontingenzkoeffizienten.
| Reaktion | |||
| gut | mittel | stark verzögert | |
| ohne Alkohol | 120 | 60 | 20 |
| mit Alkohol | 60 | 100 | 40 |
- (a)
- Bestimmen Sie die relativen und absoluten Randhäufigkeiten der Tabelle.
- (b)
- Bestimmen Sie diejenige bedingte relative Häufigkeit, die sinnvoll interpretierbar ist.
- (c)
- Bestimmen Sie den
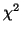 - und den (korrigierten) Kontingenzkoeffizienten.
- und den (korrigierten) Kontingenzkoeffizienten.
- (d)
- Welche relativen Chancen lassen sich aus dieser Kontingenztafel gewinnen?
| Jahr | Ertrag ( |
Clusterzahl ( |
| 1971 | 5.6 | 116.37 |
| 1973 | 3.2 | 82.77 |
| 1974 | 4.5 | 110.68 |
| 1975 | 4.2 | 97.50 |
| 1976 | 5.2 | 115.88 |
| 1977 | 2.7 | 80.19 |
| 1978 | 4.8 | 125.24 |
| 1979 | 4.9 | 116.15 |
| 1980 | 4.7 | 117.36 |
| 1981 | 4.1 | 93.31 |
| 1982 | 4.4 | 107.46 |
| 1983 | 5.4 | 122.30 |
Berechnen Sie
- (a)
- die Stichprobenmittelwerte
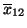 und
und
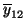 ,
,
- (b)
- den empirischen Korrelationskoeffizienten
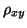 , und
, und
- (c)
- den empirischen Rang-Korrelationskoeffizienten
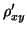 . Erstellen Sie auch einen Scatterplot der Rangstichproben.
. Erstellen Sie auch einen Scatterplot der Rangstichproben.
| Algebra (X) | 75 | 80 | 93 | 65 | 87 | 71 | 98 | 68 | 84 | 77 |
| Physik (Y) | 82 | 78 | 86 | 72 | 91 | 80 | 95 | 72 | 89 | 74 |
- (a)
- Stellen Sie die Daten graphisch dar.
- (b)
- Bestimmen Sie eine Gerade, die sich den Daten anpasst,
nach der Methode der kleinsten Quadrate, indem Sie
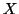 als
unabhängige Variable betrachten.
als
unabhängige Variable betrachten.
- (c)
- Bestimmen Sie eine Gerade, die sich den Daten anpasst,
nach der Methode der kleinsten Quadrate, indem Sie
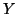 als
unabhängige Variable betrachten.
als
unabhängige Variable betrachten.
- (d)
- Wenn ein Student 75 Punkte in Algebra erhält, wie hoch ist dann seine erwartete Punktzahl in Physik?
- (e)
- Wenn ein Student 95 Punkte in Physik erhält, wie hoch ist dann seine erwartete Punktzahl in Algebra?