| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 5 | 3 | 8 | 2 | 2 | 10 | 8 | 7 | 4 | |
| 1 | 6 | 1 | 6 | 3 | 2 | 8 | 5 | 6 | 2 |
- (a)
- Was sagt das Streudiagramm über den
Zusammenhang von
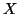 und
und 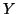 aus?
aus?
- (b)
- Passen Sie eine Gerade an die beobachteten Datenpunkte an,
unter Verwendung der Methode der kleinsten Quadrate. Beurteilen
Sie die Güte der Anpassung (Hinweis: Der empirische
Korrelationskoeffizient ist
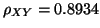 ).
).
- (c)
- Ein Patient wird mit einer Dosis von 5,5 mg des Medikaments behandelt. Welche Reaktionszeit prognostizieren Sie?
- (d)
- Wie lässt sich der in (b) geschätzte Steigungsparameter interpretieren?
- (a)
- Geben Sie Interpretation des abgebildeten Streudiagramms.
- (b)
- Bestimmen Sie für die Merkmale Clusterzahl je Traube und
Jahresertrag die Werte
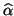 und
und
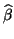 sowie
sowie
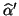 und
und
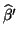 und geben Sie jeweils die zugehörige
geschätzte Geradengleichung an.
und geben Sie jeweils die zugehörige
geschätzte Geradengleichung an.
- (c)
- Prognostizieren Sie mit Hilfe der Regressionsgeraden
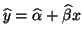 den
Jahresertrag, der einer mittleren Clusterzahl von 100 Beeren je
Traube entsprechen würde.
den
Jahresertrag, der einer mittleren Clusterzahl von 100 Beeren je
Traube entsprechen würde.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | |
| -0.09 | 2.37 | 3.14 | 4.26 | 5.48 | 4.77 | 7.3 | 6.45 | 9.14 | 11.13 | 0 |
- (a)
- Zeichnen Sie zunächst ein Streudiagramm von
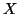 und
und 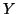 unter
Berück- sichtigung aller Daten (also auch der elften
Beobachtung).
unter
Berück- sichtigung aller Daten (also auch der elften
Beobachtung).
- (b)
- Bestimmen Sie nun beide empirische Korrelationskoeffizienten
für alle elf Daten. Verwenden Sie dabei folgende
Größen , die man bei der Berechnung der
Korrelationskoeffizienten mit lediglich den ersten zehn
Datenpunkten erhlten hat:
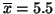 ,
,
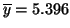 ,
,
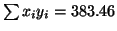 ,
,
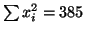 ,
,
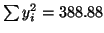 .
.
- (c)
- Interpretieren Sie die in (a) und (b) erhaltenen Ergebnisse.
| Kind |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Einkommen |
2.7 | 1.9 | 3.1 | 3.9 | 4.0 | 3.4 | 2.1 | 2.9 |
| Geburtsgewicht |
5 | 6 | 9 | 8 | 7 | 6 | 7 | 8 |
- (a)
- Tragen Sie die Beobachtungen in ein Streudiagramm ein.
- (b)
- Man möchte nun anhand des Einkommens mit Hilfe
eines linearen Regressionsmodells
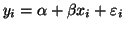 ,
, 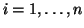 das Geburtsgewicht vorhersagen.
Schätzen Sie die Regressionsgerade und zeichnen Sie diese in
das Streudiagramm.
das Geburtsgewicht vorhersagen.
Schätzen Sie die Regressionsgerade und zeichnen Sie diese in
das Streudiagramm.
- (c)
- Ein Ehepaar verdient
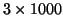 Einheiten der
Landeswährung im Monat. Welches Geburtsgewicht prognostizieren
Sie?
Einheiten der
Landeswährung im Monat. Welches Geburtsgewicht prognostizieren
Sie?
- (d)
- Berechnen Sie das Bestimmtheitsmaß. Geben Sie eine Interpretation seines Wertes und begründen Sie, ob das Einkommen zur Vorhersage des Geburtsgewichts geeignet ist.
- (a)
- Plotten Sie die Dichtefunktion der N(2,3)-Verteilung.
- (b)
- Plotten Sie die Dichtefunktion der
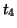 -Verteilung.
-Verteilung.
- (c)
- Lesen Sie aus der Tabelle das 0.95-Quantil
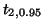 der
der
 -Verteilung ab.
-Verteilung ab.
- (d)
- Lesen Sie aus der Tabelle das 0.90-Quantil
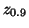 der
N(0,1)-Verteilung ab.
der
N(0,1)-Verteilung ab.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 26 | 23 | 27 | 28 | 24 | 25 | |
| 170 | 150 | 160 | 175 | 155 | 150 |
wobei die
- (a)
- Bestimmen Sie die Kleinst-Quadrat-Schätzwerte für
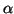 und
und 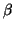 .
.
- (b)
- Schätzen Sie
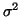 .
.
- (c)
- Sei jetzt zusätzlich die Normalverteilungsannahme vorausgesetzt,
d.h.
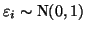 für
für 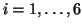 .
Führen Sie einen Test zum Niveau
.
Führen Sie einen Test zum Niveau 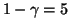 % durch
für die Hypothesen
% durch
für die Hypothesen
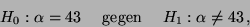
und
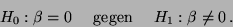
Interpretieren Sie das Ergebnis der Tests.