Prof. Dr. V. Schmidt / Dipl.-Math.oec. H. Schmidt  SS 2003´


Blatt 5´


08.07.2003´

Übungen zu Wirtschaftsstatistik
Abgabe: Dienstag, 22.07.2003, vor den Übungen

Hinweise zur Klausur
Termin: Montag, 04. August 2003 von 14.00 Uhr bis 16.00 Uhr im Hörsaal H4/5.
Mitzubringende Hilfsmittel: Schreibzeug, nichtprogrammierbarer Taschenrechner und ein DIN A4 Blatt mit Notizen.

1.

Fünf Hersteller von TV-Geräten lassen sich hinsichtlich ihrer Marktanteile in zwei Gruppen aufteilen. Drei Hersteller besitzen jeweils gleiche Marktanteile von 10 Prozent, der Rest des Marktes teilt sich unter den verbleibenden Herstellern gleichmäßig auf.

(a)

Zeichnen Sie die zugehörige Lorenzkurve und berechnen Sie den (normierten und unnormierten) Gini-Koeffizienten.

(b)

Betrachten Sie die Situation, dass in einer gewissen Zeitperiode vier der fünf Hersteller kein Großgerät verkauft haben. Zeichnen Sie die zugehörige Lorenzkurve und geben Sie den Wert des (normierten und unnormierten) Gini-Koeffizienten an.

(c)

Berechnen Sie für die Situationen in a) und b) jeweils den Herfindahl-Index 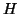$H$ (Definition siehe Blatt 2, Aufgabe 7).

2.

Betrachten Sie nochmals die Situation (stochastisches Modell der linearen Regression mit Normalverteilungsannahme der Residuen) und die Daten wie in Aufgabe 6 auf Blatt 4 beschrieben.

(a)

Geben Sie mit Hilfe der geschätzten Kleinst-Quadrate- Regressionsgeraden aus Aufgabe 6 eine Prognose für den Blutdruck eines Mannes mit einem BMI von 21.

(b)

Bestimmen Sie ein 98%-Konfidenzintervall für den erwarteten Blutdruck von Männern mit einem BMI von 21.

(c)

Bestimmen Sie ein 95%- und ein 98%-Prognoseintervall für den Blutdruck eines Mannes mit einem BMI von 21.

3.

Die folgende Tabelle enthält Daten über die Anzahl von Stunden, die 8 Studenten eines Kurses außerhalb der Vorlesungsstunden in einem Zeitraum von drei Wochen zum Lernen aufgewendet haben, sowie ihre Punktezahlen, die sie in der Prüfung am Ende dieses Zeitraumes erreicht haben.

Student aus der Stichprobe	1	2	3	4	5	6	7	8
Lernzeit in Stunden ($X$)	20	16	34	23	27	32	18	22
Punktezahl in der Prüfung ($Y$)	64	61	84	70	88	92	72	77

 

Es sei nun das stochastische Modell der linearen Regression mit Normalverteilungsannahme der Residuen zugrundegelegt.

(a)

Bestimmen Sie die Kleinst-Quadrate-Regressionsgerade für die angegebenen Daten. Tragen Sie diese zusammen mit den Daten in ein Streuungsdiagramm ein.

(b)

Testen Sie auf dem Ein-Prozent-Signifikanzniveau die Nullhypothese, dass die Steigung der Regressionsgeraden Null ist und interpretieren Sie das Ergebnis.

(c)

Prognostizieren Sie mit Hilfe der Regressionsgleichung aus Teil (a) das Prüfungsergebnis eines Studenten, der 30 Stunden für das Studium des Kursmaterials verwendet hat.

(d)

Bestimmen Sie ein 90%-Konfidenzintervall für die mittlere Prüfungsnote von Studenten, die 30 Stunden gelernt haben.

(e)

Bestimmen Sie ein 90%-Prognoseintervall für die Prüfungsnote eines einzelnen Studenten, der 30 Stunden für die Vorbereitung verwendet hat.

4.

Beobachtet wurden das Jahreseinkommen $X$ (in 10Tsd. EUR) und der Kartoffelverbrauch $Y$ (in kg) in zehn zufällig ausgewählten Haushalten. Dabei wurden die folgenden Wertepaare $(x_i,y_i)$, $i=1,...,10$, erhoben:

$~i~~$	1	2	3	4	5	6	7	8	9	10
$x_i$	8.5	7.8	7.5	6.2	6.5	6.0	5.6	4.6	4.0	3.3
$y_i$	18	20	20	25	29	31	33	37	43	44

 

Es sei wie in der vorhergehenden Aufgabe das stochastische Modell der linearen Regression mit Normalverteilungsannahme der Residuen zugrundegelegt.

(a)

Testen Sie zum Niveau 0.05 die Nullhypothese, dass die Regressionskonstante gleich 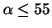$\alpha \leq 55$ ist.

(b)

Bestimmen Sie 95%-Konfidenzintervalle der Parameter 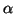$\alpha$ und $\beta$.

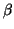(c)

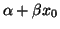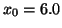Geben Sie ein 95%-Konfidenzintervall für den erwarteten Zielwert $\alpha + \beta x_0$ mit $x_0 = 6.0$ an.

(d)

Bestimmen Sie zum Niveau 0.05 ein Konfidenzband für die Regressionsgerade $y = \alpha + \beta x$.

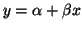(e)

Erstellen Sie mit Maple ein Diagramm, welches die Wertepaare, die Kleinst-Quadrate-Regressionsgerade sowie das Konfidenzband aus Teil (d) enthält. Tragen Sie das Konfidenzintervall aus Teil (c) in das Diagramm ein (Tip: Maple-Befehl RegBand).

5.

An einem Versuch, bei dem die Auswirkungen von 4 verschiedenen Werbemethoden $W_1,\ldots,W_4$ auf den Absatz von Zweirädern untersucht werden soll, nehmen 15 Zweiradgeschäfte teil. Die folgende Tabelle stellt die Absätze geordnet nach eingesetzter Werbemethode dar.

Werbemethode	Absatz
$W_1$	41    44    42
$W_2$	52    54    59    49
$W_3$	48    38    45    50    34
$W_4$	46    61    47

Es sei das Modell der einfaktoriellen Varianzanalyse zugrundegelegt, d.h. $Y_{ij} = \theta_i + \varepsilon_{ij}$ für $i=1,\ldots,k$ und $j=1,\ldots,n_i$, wobei $\varepsilon_{ij}\sim\mbox{N}(0,\sigma^2)$ (d.h. es gelte auch die Annahme der Homoskedastizität).

(a)

Testen Sie mit den Daten aus der Tabelle auf dem Fünf-Prozent-Signifikanz- niveau die Nullhypothese, dass sich der erwartete Absatz durch die vier verschiedenen Werbemethoden nicht signifikant unterscheidet.

(b)

Fällen Sie die Testentscheidung für den Test aus (a) mit Hilfe von MAPLE (Tip: Funktion Anova1).

6.

15 Trainees einer Großbank werden für eine bestimmte Unterrichtseinheit zufällig drei verschiedenen Mentoren $M_1,M_2,M_3$ zugeteilt, die Ihnen Kenntnisse eines speziellen Fachgebietes vermitteln sollen. Folgende Tabelle gibt die erzielten Punktezahlen der Trainees bei einem Leistungstest am Ende der Unterrichtseinheit wieder.

Mentor	Punktezahlen
$M_1$	86    79    81    78    84
$M_2$	90    85    88    83    89
$M_3$	75    78    73    71    72

Legen Sie das gleiche Modell wie in der vorhergehenden Aufgabe zugrunde.

(a)

Testen Sie auf dem Fünf-Prozent-Signifikanzniveau die Nullhypothese, dass die drei Stichprobenmittelwerte 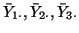$\bar{Y}_{1\cdot},\bar{Y}_{2\cdot},\bar{Y}_{3\cdot}$ aus der selben Grundgesamtheit stammen. Interpretieren Sie das Ergebnis.

(b)

Berechnen Sie die Gesamtvariabilität der Daten, die Variabilität zwischen den Stufen sowie die Variabilität innerhalb der Stufen des Einflußfaktors an. Überprüfen Sie die Gültigkeit der Quadratsummenzerlegung anhand Ihrer Ergebnisse.