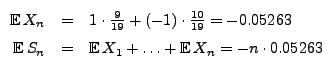Next: Ereignisse und Wahrscheinlichkeiten
Up: Einleitung
Previous: Typische Fragestellungen und Ergebnisse
Contents
Betrachten Roulette-Spiel mit
38 möglichen Ausgängen, nämlich 18 rote Felder, 18 schwarze Felder und
2 grüne
Felder. Betrachten Spieler, der auf ,,Rot'' setzt. Er gewinnt 1 Euro mit
der Wahrscheinlichkeit
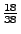 und verliert 1 Euro mit der
Wahrscheinlichkeit
und verliert 1 Euro mit der
Wahrscheinlichkeit
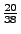 .
Sei nun
.
Sei nun 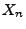 der zufällige ,,Gewinn'' beim
der zufällige ,,Gewinn'' beim  -ten
Spiel. Dann gilt:
Die Zufallsgrößen
-ten
Spiel. Dann gilt:
Die Zufallsgrößen
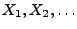 sind
unabhängig und identisch
verteilt. Betrachten Gesamtgewinn
sind
unabhängig und identisch
verteilt. Betrachten Gesamtgewinn
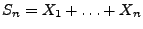 aus den ersten
aus den ersten  Spielen. Die Folge
Spielen. Die Folge
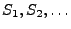 heißt Random Walk.
heißt Random Walk.
Wie groß ist der erwartete Gewinn
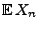 beim
beim  -ten
Spiel? Wie groß ist der erwartete Gesamtgewinn
-ten
Spiel? Wie groß ist der erwartete Gesamtgewinn
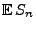 aus den ersten
aus den ersten  Spielen? Es gilt:
Spielen? Es gilt:
(Schwaches) Gesetz der großen Zahlen ,,Für große
,,Für große
 ist
ist
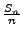 nahe bei
nahe bei
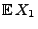 mit hoher
Wahrscheinlichkeit.''
mit hoher
Wahrscheinlichkeit.''
Zentraler Grenzwertsatz ,,Für große
,,Für große  lässt
sich
die Wahrscheinlichkeit
lässt
sich
die Wahrscheinlichkeit
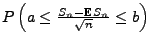 durch die Normalverteilung approximieren, wobei
durch die Normalverteilung approximieren, wobei
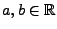 mit
mit 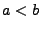 beliebige,
jedoch fest vorgegebene Toleranzgrenzen sind.''
beliebige,
jedoch fest vorgegebene Toleranzgrenzen sind.''
- Beachte
-
Den Begriffsbildungen ,,Zufallsgröße'',
,,unabhängig'', ,,identisch verteilt'', ,,für große
 '', ,,nahe
bei
'', ,,nahe
bei
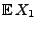 '', ,,mit hoher Wahrscheinlichkeit'' bzw.
,,Normalverteilung'' liegen mathematische Definitionen
zugrunde. Sie gehören zu den Grundbegriffen der
Stochastik, die in den folgenden Abschnitten detailliert
erläutert werden.
'', ,,mit hoher Wahrscheinlichkeit'' bzw.
,,Normalverteilung'' liegen mathematische Definitionen
zugrunde. Sie gehören zu den Grundbegriffen der
Stochastik, die in den folgenden Abschnitten detailliert
erläutert werden.




Next: Ereignisse und Wahrscheinlichkeiten
Up: Einleitung
Previous: Typische Fragestellungen und Ergebnisse
Contents
Ursa Pantle
2004-05-10
![]() beim
beim ![]() -ten
Spiel? Wie groß ist der erwartete Gesamtgewinn
-ten
Spiel? Wie groß ist der erwartete Gesamtgewinn
![]() aus den ersten
aus den ersten ![]() Spielen? Es gilt:
Spielen? Es gilt: