Solving a System of Linear Equations
In the following we show some examples for solving a system of linear equations using a LU-factorization. The coefficient matrix in all examples will be a regular, square, non-symmetric matrix:
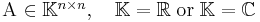
Theoretical background of the LU-factorization
Let us first recall how to apply the LU-factorization for solving the system of linear equations given by
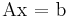
Using Gaussian elimination one can find a permutation matrix P, a lower unit triangular matrix L and an upper triangular matrix U such that
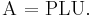
This constitutes the LU factorization of A. Thus, solving Ax=b is equivalent to solving
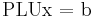
which can be done in three steps:

Implementation background of the LU-factorization
Permutation matrix P is defined through row-interchanges carried out during the factorization. Therefore a favorable representation of P is a vector p containing the pivot indices. A pivot vector
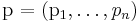
documents that during the factorization the i-th row was interchanged with the pi-th row (more formally, p stores a sequence of transpositions and their composition gives the permutation P). An implementation can compute
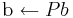
efficiently in a single loop:
for i = 1,..,n swap b(i) and b(p(i))
Traversing the same loop backwards allows one to compute the inverse permutation
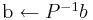
analogously through
for i = n,..,1 swap b(i) and b(p(i))
Note that this means: no extra vector is needed for storing the permutation of b instead vector b gets overwritten with P-1b.
The coefficient matrix A can be overwritten with L and U during the factorization, that is
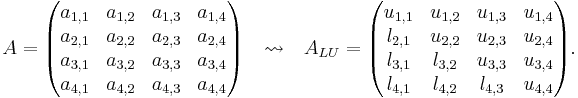
This is due to the fact that L is a lower unit triangular matrix, that means contains only ones on the diagonal. The total number of floating-point operation is of order
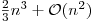 .
.
Brief summary:
LU-factorization Input: A coefficient matrix Output: A overwritten with the LU factorization P integer valued vector containing the pivots
Relevant routines in FLENS
The names of the functions are derived from corresponding LAPACK routines.
-
Description:
template <typename MA, typename MB> int sv(GeMatrix<MA> &A, DenseVector<Array<int> > &P, GeMatrix<MB> &B);
-
Description:
template <typename MA, typename VB> int sv(GeMatrix<MA> &A, DenseVector<Array<int> > &P, DenseVector<VB> &B);
-
Description: computes the LU factorization of A
template <typename FS> int trf(GeMatrix<FS> &A, DenseVector<Array<int> > &P);
-
Description: forward and backward substitution for multiple right-hand sides, i.e. solves
template <typename MA, typename MB> int trs(Transpose trans, const GeMatrix<MA> &LU, const DenseVector<Array<int> > &P, GeMatrix<MB> &B);
where PLU resulted from a LU factorization.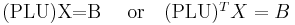
Input:
Output:
Returns: -
Description: forward and backward substitution; multiple right-hand sides.
template <typename MA, typename VB> int trs(Transpose trans, const GeMatrix<MA> &LU, const DenseVector<Array<int> > &P, DenseVector<VB> &B);
Examples Overview
The examples will briefly cover the following cases:
- Single right-hand side, i.e. solve
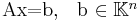
- Multiple right-hand sides, i.e. solve
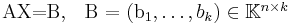
Single Right-hand Side: Solve A*x=b
We choose as coefficient matrix
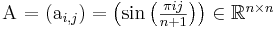
which is known from the discrete sine transform. Hence we already know what solution we get when choosing
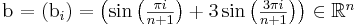
as the right-hand side: That's right, it should be
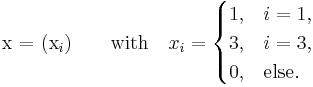
#include <flens/flens.h>
using namespace flens;
using namespace std;
typedef GeMatrix<FullStorage<double, ColMajor> > DGeMatrix;
typedef DenseVector<Array<double> > DDenseVector;
typedef DenseVector<Array<int> > IDenseVector;
int
main()
{
int n = 4;
// setup a coefficient matrix
DGeMatrix A(n,n);
Index i,j;
A(i,j) = sin(M_PI*i*j/(n+1));
// setup a right-hand side
DDenseVector b(n);
b(i) = sin(M_PI*i/(n+1)) + 3*sin(3*M_PI*i/(n+1));
// display A and b
cout << "A = " << A << endl;
cout << "b = " << b << endl;
// solve A*x = b using a LU decomposition:
// b gets overwritten with the solution x
// P contains afterwards the pivot indices used in the LU factorization
IDenseVector P(n);
sv(A, P, b);
cout << "x = A^{-1}*b = " << b << endl;
}
And here the result:
A = [4, 4]
0.587785 0.951057 0.951057 0.587785 ;
0.951057 0.587785 -0.587785 -0.951057 ;
0.951057 -0.587785 -0.587785 0.951057 ;
0.587785 -0.951057 0.951057 -0.587785 ;
b = [ 3.440955 -0.812299 -0.812299 3.440955 ]
x = A^{-1}*b = [ 1.000000 -0.000000 3.000000 0.000000 ]