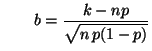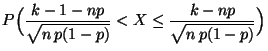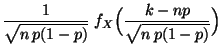Next: Zufallsvektoren
Up: Verteilung von Zufallsvariablen
Previous: Grundlegende Klassen diskreter Verteilungen
Contents
Verteilungsfunktion; absolutstetige Zufallsvariable
Sei
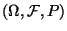 ein beliebiger Wahrscheinlichkeitsraum und
ein beliebiger Wahrscheinlichkeitsraum und
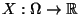 eine beliebige Zufallsvariable.
eine beliebige Zufallsvariable.
- Definition 3.5
 Die Funktion
Die Funktion
![$ F_{X}:\mathbb{R}\rightarrow [0,1]$](img311.png) mit
mit
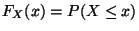 heißt Verteilungsfunktion von
heißt Verteilungsfunktion von  .
.
- Eigenschaften von Verteilungsfunktionen
-
- Asymptotisches Verhalten im Unendlichen:
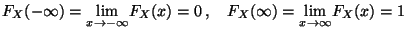
- Monotonie:

- Rechtsstetigkeit:
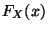 ist rechtsseitig stetig, d.h. für jede Folge
ist rechtsseitig stetig, d.h. für jede Folge
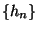 mit
mit
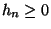 und
und
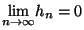 gilt
gilt
- Beachte
-
- Mit Hilfe der Verteilungsfunktion
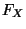 lassen sich auch
die folgenden Wahrscheinlichkeiten ausdrücken
denn es gilt beispielsweise
lassen sich auch
die folgenden Wahrscheinlichkeiten ausdrücken
denn es gilt beispielsweise
- Im allgemeinen gilt jedoch nicht
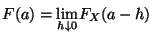 .
.
- Für die Verteilungsfunktion
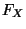 einer diskreten Zufallsvariable
einer diskreten Zufallsvariable
 gilt für jedes
gilt für jedes
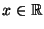 :
:
wobei
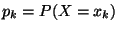 .
.
- Die Verteilungsfunktion
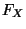 einer diskreten
Zufallsvariablen
einer diskreten
Zufallsvariablen  ist eine sogenannte Treppenfunktion, d.h. eine stückweise konstante Funktion
mit der Sprunghöhe
ist eine sogenannte Treppenfunktion, d.h. eine stückweise konstante Funktion
mit der Sprunghöhe 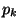 im Punkt
im Punkt 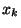 .
.
- Definition 3.6
 Die Zufallsvariable
Die Zufallsvariable
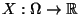 (bzw. ihre Verteilung) heißt absolutstetig,
falls die Verteilungsfunktion
(bzw. ihre Verteilung) heißt absolutstetig,
falls die Verteilungsfunktion 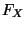 von
von  die folgende
Integraldarstellung
die folgende
Integraldarstellung
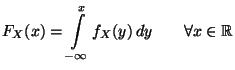 |
(3) |
besitzt, wobei
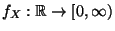 eine (integrierbare) Funktion
mit nichtnegativen Werten ist, die Dichte (bzw. Wahrscheinlichkeitsdichte) von
eine (integrierbare) Funktion
mit nichtnegativen Werten ist, die Dichte (bzw. Wahrscheinlichkeitsdichte) von  genannt wird.
genannt wird.
- Beachte
-
- Die Verteilungsfunktion
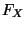 (und damit auch die Verteilung
(und damit auch die Verteilung 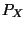 )
einer absolutstetigen Zufallsgröße
)
einer absolutstetigen Zufallsgröße  wird eindeutig durch die
Dichte
wird eindeutig durch die
Dichte 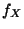 bestimmt.
bestimmt.
- Bei vielen Anwendungen ist die Dichte
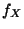 eine (zumindest
stückweise) stetige Funktion. Das Integral in der
Definitionsgleichung (3) ist dann ein
gewöhnliches Riemann-Integral.
eine (zumindest
stückweise) stetige Funktion. Das Integral in der
Definitionsgleichung (3) ist dann ein
gewöhnliches Riemann-Integral.
- Falls
 absolutstetig ist, dann hat die
Verteilungsfunktion
absolutstetig ist, dann hat die
Verteilungsfunktion 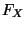 keine Sprünge, d.h.,
keine Sprünge, d.h., 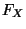 ist eine
(im üblichen Sinne) stetige Funktion. Hieraus folgt
insbesondere, daß
ist eine
(im üblichen Sinne) stetige Funktion. Hieraus folgt
insbesondere, daß
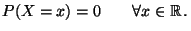 |
(4) |
Beweis von (4). Es gilt
Es gilt
- Die Verteilungsfunktion
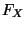 einer absolutstetigen
Zufallsvariablen
einer absolutstetigen
Zufallsvariablen  ist jedoch im allgemeinen nicht
überall differenzierbar. Und zwar ist
ist jedoch im allgemeinen nicht
überall differenzierbar. Und zwar ist 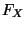 dort nicht
differenzierbar, wo die Dichte
dort nicht
differenzierbar, wo die Dichte 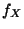 Sprungstellen hat.
Sprungstellen hat.
- Beispiele
 Um die Verteilung einer absolutstetigen
Zufallsvariable
Um die Verteilung einer absolutstetigen
Zufallsvariable  zu beschreiben,
genügt es, die Dichte
zu beschreiben,
genügt es, die Dichte 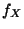 zu betrachten, weil durch
zu betrachten, weil durch 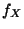 die
Verteilungsfunktion
die
Verteilungsfunktion 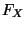 und damit auch die Verteilung
und damit auch die Verteilung 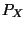 von
von  eindeutig bestimmt wird.
eindeutig bestimmt wird.
- Normalverteilung N
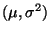 mit den
Parametern
mit den
Parametern
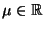 und
und
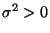 :
:
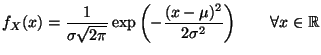 |
(5) |
Spezialfall: Standardnormalverteilung N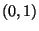 . Dann
nimmt die Dichte
. Dann
nimmt die Dichte  in (5) die folgende Form
an:
in (5) die folgende Form
an:
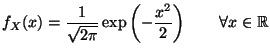 |
(6) |
- Exponentialverteilung Exp
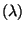 mit Parameter
mit Parameter
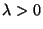 :
:
- Gleichverteilung U
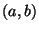 mit den Parametern
mit den Parametern
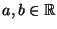 , wobei
, wobei 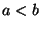 :
:
- Beachte
-




Next: Zufallsvektoren
Up: Verteilung von Zufallsvariablen
Previous: Grundlegende Klassen diskreter Verteilungen
Contents
Roland Maier
2001-08-20
![]() ein beliebiger Wahrscheinlichkeitsraum und
ein beliebiger Wahrscheinlichkeitsraum und
![]() eine beliebige Zufallsvariable.
eine beliebige Zufallsvariable.
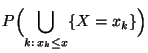
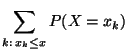
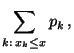
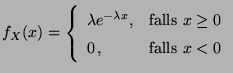
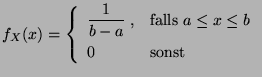
 und
und