



Next: Stochastische Unabhängigkeit
Up: Bedingte Wahrscheinlichkeiten
Previous: Formel der totalen Wahrscheinlichkeit;
Contents
Bedingte Verteilung; bedingte Dichte
In Übereinstimmung mit Definition 3.11 ist die folgende
Sprechweise üblich.
- Definition 3.15
-
- Sei
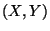 ein diskreter Zufallsvektor mit
ein diskreter Zufallsvektor mit
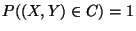 für
eine abzählbare Menge
für
eine abzählbare Menge
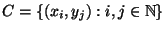 .
Für jedes
.
Für jedes
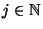 mit
mit
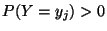 heißt dann
heißt dann
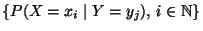 die bedingte
Wahrscheinlichkeitsfunktion von
die bedingte
Wahrscheinlichkeitsfunktion von  unter der Bedingung
unter der Bedingung
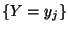 . Sie bestimmt die bedingte
Verteilung
. Sie bestimmt die bedingte
Verteilung
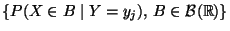 von
von  unter der Bedingung
unter der Bedingung 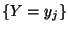 eindeutig.
eindeutig.
- Analog heißt
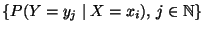 bzw.
bzw.
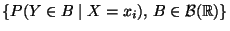 für jedes
für jedes
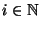 mit
mit
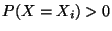 die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von
die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von 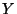 unter der Bedingung
unter der Bedingung 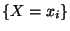 .
.
- Wenn
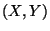 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
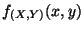 ist, dann heißt die
Funktion
ist, dann heißt die
Funktion
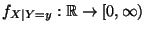 mit
die bedingte Dichte von
mit
die bedingte Dichte von  unter der Bedingung
unter der Bedingung
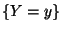 , wobei
, wobei 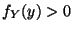 vorausgesetzt wird.
vorausgesetzt wird.
- Analog heißt die Funktion
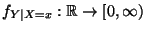 mit
die bedingte Dichte von
mit
die bedingte Dichte von 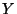 unter der Bedingung
unter der Bedingung 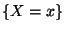 ,
wobei
,
wobei 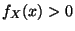 vorausgesetzt wird.
vorausgesetzt wird.
- Beispiele
-
- zweimaliges Würfeln
Sei
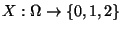 bzw.
bzw.
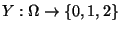 die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von
die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von  unter der Bedingung
unter der Bedingung 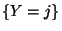 :
:
- integrierte Gleichverteilung
Sei 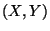 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für ![$ y\in[0,1]$](img545.png) gilt dann für die bedingte Dichte von
gilt dann für die bedingte Dichte von  unter der Bedingung
unter der Bedingung
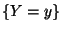 :
Die bedingte Dichte
:
Die bedingte Dichte
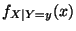 stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte
stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte 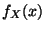 von
von  überein; vgl.
Abschnitt 3.3.3.
überein; vgl.
Abschnitt 3.3.3.




Next: Stochastische Unabhängigkeit
Up: Bedingte Wahrscheinlichkeiten
Previous: Formel der totalen Wahrscheinlichkeit;
Contents
Roland Maier
2001-08-20
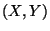 ein diskreter Zufallsvektor mit
ein diskreter Zufallsvektor mit
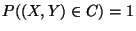 für
eine abzählbare Menge
für
eine abzählbare Menge
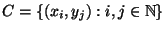 .
Für jedes
.
Für jedes
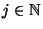 mit
mit
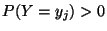 heißt dann
heißt dann
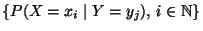 die bedingte
Wahrscheinlichkeitsfunktion von
die bedingte
Wahrscheinlichkeitsfunktion von  unter der Bedingung
unter der Bedingung
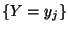 . Sie bestimmt die bedingte
Verteilung
. Sie bestimmt die bedingte
Verteilung
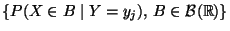 von
von  unter der Bedingung
unter der Bedingung 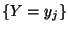 eindeutig.
eindeutig.
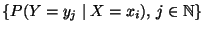 bzw.
bzw.
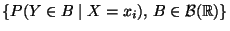 für jedes
für jedes
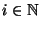 mit
mit
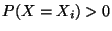 die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von
die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von 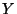 unter der Bedingung
unter der Bedingung 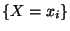 .
.
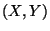 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
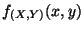 ist, dann heißt die
Funktion
ist, dann heißt die
Funktion
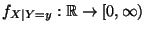 mit
die bedingte Dichte von
mit
die bedingte Dichte von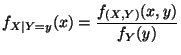
 unter der Bedingung
unter der Bedingung
 , wobei
, wobei  vorausgesetzt wird.
vorausgesetzt wird.
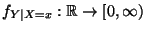 mit
die bedingte Dichte von
mit
die bedingte Dichte von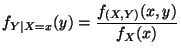
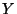 unter der Bedingung
unter der Bedingung 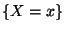 ,
wobei
,
wobei 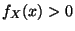 vorausgesetzt wird.
vorausgesetzt wird.
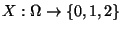 bzw.
bzw.
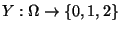 die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von
die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von  unter der Bedingung
unter der Bedingung 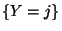 :
:
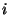
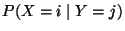
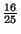
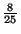
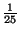
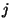
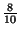
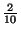
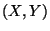 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für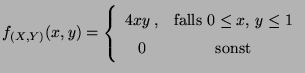
![$ y\in[0,1]$](img545.png) gilt dann für die bedingte Dichte von
gilt dann für die bedingte Dichte von  unter der Bedingung
unter der Bedingung
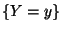 :
Die bedingte Dichte
:
Die bedingte Dichte![$\displaystyle f_{X\mid Y=y}(x)=\frac{f_{(X,Y)}(x,y)}{f_Y(y)}=
\left\{\begin{array}{cc}
2x\,,&\mbox{falls $x\in[0,1]$}\\
0&\mbox{sonst}
\end{array}\right.
$](img546.png)
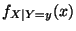 stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte
stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte 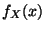 von
von  überein; vgl.
Abschnitt 3.3.3.
überein; vgl.
Abschnitt 3.3.3.