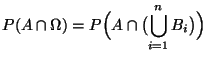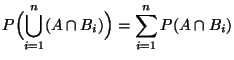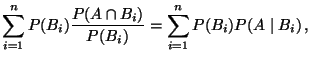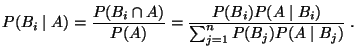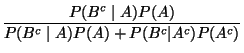Next: Bedingte Verteilung; bedingte Dichte
Up: Bedingte Wahrscheinlichkeiten
Previous: Definition und Multiplikationssatz
Contents
Formel der totalen Wahrscheinlichkeit; Bayessche
Formel
Sei
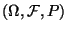 ein beliebiger Wahrscheinlichkeitsraum.
ein beliebiger Wahrscheinlichkeitsraum.
Bei der Berechnung der Wahrscheinlichkeit 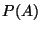 eines Ereignisses
eines Ereignisses
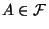 ist es manchmal nützlich, die (unbedingte)
Wahrscheinlichkeit
ist es manchmal nützlich, die (unbedingte)
Wahrscheinlichkeit 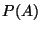 als gewichtete Summe von bedingten
Wahrscheinlichkeiten darzustellen.
als gewichtete Summe von bedingten
Wahrscheinlichkeiten darzustellen.
Hierfür ist es erforderlich, den Grundraum 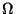 wie folgt in
(meßbare) Teilmengen zu zerlegen.
wie folgt in
(meßbare) Teilmengen zu zerlegen.
- Definition 3.13
 Sei
Sei
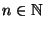 eine beliebige natürliche Zahl, und sei
eine beliebige natürliche Zahl, und sei
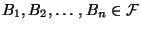 eine (endliche) Folge von Ereignissen mit
den Eigenschaften
eine (endliche) Folge von Ereignissen mit
den Eigenschaften
- (Z1)
-
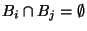 für
für 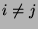 ,
,
- (Z2)
-
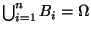 ,
,
- (Z3)
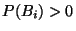 für alle
für alle
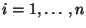 .
.
Dann heißt
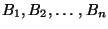 meßbare Zerlegung von
meßbare Zerlegung von
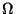 .
.
- Theorem 3.14
 Sei
Sei
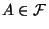 ein beliebiges Ereignis und
ein beliebiges Ereignis und
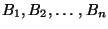 eine meßbare Zerlegung von
eine meßbare Zerlegung von
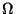 . Dann gilt
. Dann gilt
- Formel der totalen Wahrscheinlichkeit
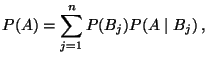 |
(14) |
- Bayessche Formel
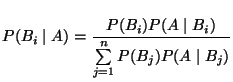 |
(15) |
für jedes
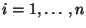 , wobei in (15) vorausgesetzt
wird, daß
, wobei in (15) vorausgesetzt
wird, daß 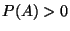 .
.
- Beweis
 Aus (Z1)-(Z3) und aus der Additivität des
Wahrscheinlichkeitsmaßes
Aus (Z1)-(Z3) und aus der Additivität des
Wahrscheinlichkeitsmaßes 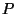 ergibt sich, daß
ergibt sich, daß
wobei im letzten Schritt die Definitionsgleichung
(12) benutzt wird. Damit ist (14)
bewiesen. Aus (12) und (14) ergibt
sich nun
- Beachte
 Die Aussagen von Theorem 3.14 bleiben gültig,
wenn anstelle einer Zerlegung von
Die Aussagen von Theorem 3.14 bleiben gültig,
wenn anstelle einer Zerlegung von 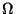 in endlich viele
Teilmengen eine unendliche Folge
in endlich viele
Teilmengen eine unendliche Folge
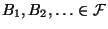 von Ereignissen mit den Eigenschaften
von Ereignissen mit den Eigenschaften
- (Z'1)
-
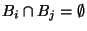 für
für 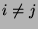 ,
,
- (Z'2)
-
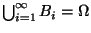 ,
,
- (Z'3)
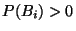 für alle
für alle
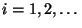
betrachtet wird. Die Formeln (14) und
(15) sind dann lediglich wie folgt zu modifizieren:
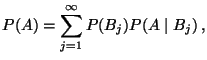 |
(16) |
bzw.
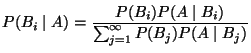 |
(17) |
für jedes
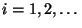 , wobei in (17) erneut
vorausgesetzt wird, daß
, wobei in (17) erneut
vorausgesetzt wird, daß 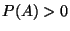 .
.
- Beispiel
-
- Betrachten eine Fußballmannschaft, deren
Siegeschance je Bundesliga-Spiel bei 75% liegt, falls ihr
Kapitän in guter Form ist.
- Falls ihr Kapitän jedoch
nicht in guter Form ist, dann betrage ihre
Siegeschance nur 40%.
- Bei 70% aller Bundesliga-Spiele
seiner Mannschaft sei der Kapitän in guter Form.
- Gesucht ist die Wahrscheinlichkeit, daß
- die Mannschaft ein Bundesliga-Spiel gewinnt,
- der Kapitän bei einem Bundesliga-Spiel in guter Form
ist, obwohl die Mannschaft das Spiel nicht gewinnt.
- Lösung: Zerlegen den Grundraum
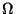 auf zwei verschiedene
Weisen in zwei Komponenten.
auf zwei verschiedene
Weisen in zwei Komponenten.
- Sei
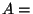 {Kapitän ist in guter Form},
{Kapitän ist in guter Form},
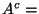 {Kapitän ist nicht in guter Form}
{Kapitän ist nicht in guter Form}
bzw.
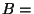 {Mannschaft gewinnt Bundesliga-Spiel},
{Mannschaft gewinnt Bundesliga-Spiel},
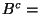 {Mannschaft gewinnt Bundesliga-Spiel nicht}
{Mannschaft gewinnt Bundesliga-Spiel nicht}
- Dann gilt
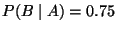 ,
,
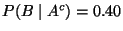 ,
,
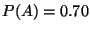
- Aus (14) bzw. (15) ergibt
sich nun
bzw.




Next: Bedingte Verteilung; bedingte Dichte
Up: Bedingte Wahrscheinlichkeiten
Previous: Definition und Multiplikationssatz
Contents
Roland Maier
2001-08-20
![]() ein beliebiger Wahrscheinlichkeitsraum.
ein beliebiger Wahrscheinlichkeitsraum.
![]() eines Ereignisses
eines Ereignisses
![]() ist es manchmal nützlich, die (unbedingte)
Wahrscheinlichkeit
ist es manchmal nützlich, die (unbedingte)
Wahrscheinlichkeit ![]() als gewichtete Summe von bedingten
Wahrscheinlichkeiten darzustellen.
als gewichtete Summe von bedingten
Wahrscheinlichkeiten darzustellen.
![]() wie folgt in
(meßbare) Teilmengen zu zerlegen.
wie folgt in
(meßbare) Teilmengen zu zerlegen.