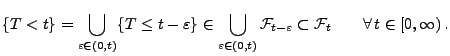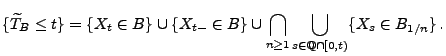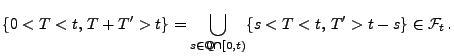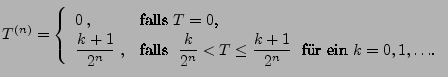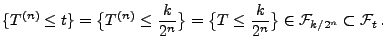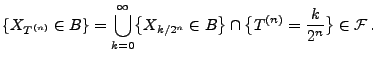Nächste Seite: Submartingale und Supermartingale; Beispiele
Aufwärts: Martingale
Vorherige Seite: Martingale
Inhalt
Filtrationen und Stoppzeiten
- Definition
 Sei
Sei
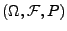 ein vollständiger
Wahrscheinlichkeitsraum.
ein vollständiger
Wahrscheinlichkeitsraum.
- Eine Familie
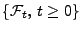 von Teil-
von Teil-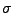 -Algebren
von
-Algebren
von
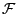 heißt Filtration, wenn
heißt Filtration, wenn
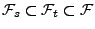 für beliebige
für beliebige 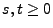 mit
mit
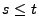 gilt.
gilt.
- Die Filtration
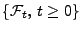 heißt vollständig,
wenn
heißt vollständig,
wenn
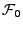 (und damit auch
(und damit auch
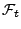 für jedes
für jedes 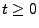 )
sämtliche Nullmengen enthält.
)
sämtliche Nullmengen enthält.
- Die Filtration
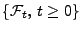 heißt rechtsstetig,
wenn
heißt rechtsstetig,
wenn
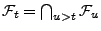 für jedes
für jedes 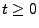 .
.
- Sei
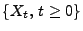 ein stochastischer Prozess über
ein stochastischer Prozess über
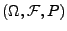 , und für jedes
, und für jedes 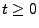 sei
sei
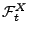 die
kleinste
die
kleinste 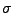 -Algebra, für die
für beliebige
-Algebra, für die
für beliebige 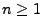 ,
,
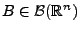 und
und
![$ t_1,\ldots,t_n\in[0,t]$](img1588.png) gilt. Dann heißt
gilt. Dann heißt
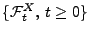 die natürliche Filtration, die von
die natürliche Filtration, die von 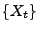 erzeugt wird.
erzeugt wird.
- Sei
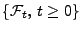 eine beliebige Filtration, und sei
eine beliebige Filtration, und sei
![$ T:\Omega\to[0,\infty]$](img1590.png) eine beliebige Zufallsvariable über
eine beliebige Zufallsvariable über
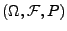 . Man sagt, dass
. Man sagt, dass 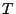 eine Stoppzeit
(bezüglich der Filtration
eine Stoppzeit
(bezüglich der Filtration
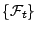 ) ist, wenn
) ist, wenn
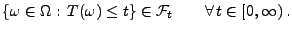 |
(1) |
- Beachte
 Wir werden stets (o.B.d.A.)
voraussetzen, dass die jeweils betrachtete Filtration
Wir werden stets (o.B.d.A.)
voraussetzen, dass die jeweils betrachtete Filtration
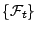 vollständig ist.
vollständig ist.
Lemma 3.5

Sei
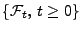
eine rechtsstetige Filtration. Die
Zufallsvariable
![$ T:\Omega\to[0,\infty]$](img1590.png)
ist genau dann eine
Stoppzeit, wenn
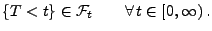 |
(2) |
- Beweis

- Für jedes
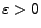 gilt offenbar, dass
gilt offenbar, dass
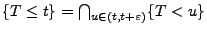 .
.
- Aus (2) und aus der Rechtsstetigkeit der
Filtration
 ergibt sich somit, dass
ergibt sich somit, dass
- Sei nun
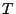 eine Stoppzeit. Dann gilt
eine Stoppzeit. Dann gilt

- Definition
 Sei
Sei
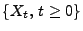 ein stochastischer Prozess über dem
Wahrscheinlichkeitsraum
ein stochastischer Prozess über dem
Wahrscheinlichkeitsraum
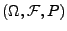 mit der Filtration
mit der Filtration
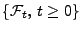 .
Man sagt, dass der Prozess
.
Man sagt, dass der Prozess 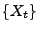 adaptiert (bezüglich der Filtration
adaptiert (bezüglich der Filtration
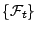 ) ist, wenn
) ist, wenn
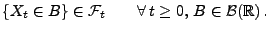 |
(3) |
Außerdem heißt die Abbildung
![$ T_B:\Omega\to[0,\infty]$](img1599.png) mit
mit
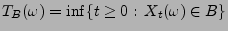 die Ersterreichungszeit der Borel-Menge
die Ersterreichungszeit der Borel-Menge
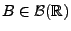 durch den
Prozess
durch den
Prozess 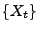 .
.
Für ,,càdlàg'' Prozesse, deren Trajektorien mit
Wahrscheinlichkeit 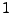 rechtsstetige Funktionen mit linksseitigen
Grenzwerten sind (vgl. Abschnitt 1.4), diskutieren
wir nun einige Beispiele von Stoppzeiten.
rechtsstetige Funktionen mit linksseitigen
Grenzwerten sind (vgl. Abschnitt 1.4), diskutieren
wir nun einige Beispiele von Stoppzeiten.
Theorem 3.6

Sei
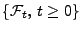
eine
rechtsstetige Filtration und sei
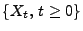
ein
adaptierter càdlàg Prozess. Für jede offene Menge
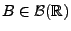
ist dann die Ersterreichungszeit
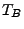
eine
Stoppzeit. Wenn
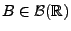
eine abgeschlossene Menge ist,
dann ist die Abbildung
![$ \widetilde T_B:\Omega\to[0,\infty]$](img1602.png)
mit
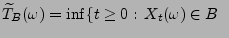
oder
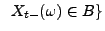
eine Stoppzeit, wobei
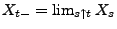
.
- Beweis

- Sei
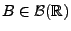 zunächst eine offene Menge.
zunächst eine offene Menge.
- Sei nun
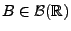 eine abgeschlossene Menge.
eine abgeschlossene Menge.
Theorem 3.7

Seien
![$ T,T^\prime:\Omega\to[0,\infty]$](img1615.png)
beliebige Stoppzeiten. Dann sind auch
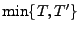
,
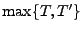
,
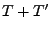
bzw.
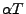
für jedes
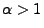
Stoppzeiten.
- Beweis

- Weil
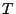 und
und 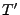 Stoppzeiten sind, gilt
Stoppzeiten sind, gilt
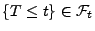 bzw.
bzw.
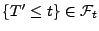 und somit
d.h.,
und somit
d.h.,
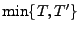 ist eine Stoppzeit.
ist eine Stoppzeit.
- Völlig analog ergibt sich, dass
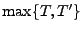 ein Stoppzeit
ist, denn aus
ein Stoppzeit
ist, denn aus
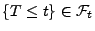 und
und
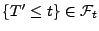 folgt, dass
folgt, dass
- Um zu zeigen, dass auch
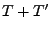 eine Stoppzeit ist, genügt es
zu zeigen, dass
eine Stoppzeit ist, genügt es
zu zeigen, dass
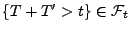 für jedes
für jedes 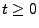 .
.
- Dies ergibt sich aus der Identität
- Denn es ist klar, dass die ersten drei Ereignisse auf der rechten
Seite der letzten Gleichheit zu
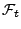 gehören,
gehören,
- und für das vierte Ereignis gilt
- Außerdem gilt für jedes
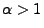 , dass
, dass
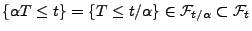 .
.

Manchmal ist es nützlich, beliebige (nichtnotwendig diskrete)
Stoppzeiten durch monotone Folgen von Stoppzeiten zu
approximieren, die jeweils nur abzählbar unendlich viele Werte mit
positiver Wahrscheinlichkeit annehmen können. Aus dem Beweis des
folgenden Theorems ergibt sich, wie eine solche monotone Folge von
diskreten Stoppzeiten konstruiert werden kann.
Theorem 3.8
Sei
![$ T:\Omega\to(0,\infty]$](img1630.png)
eine beliebige endliche Stoppzeit über
dem Wahrscheinlichkeitsraum
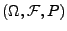
, d.h., es gelte
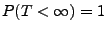
. Dann gibt es eine Folge
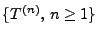
von diskreten Stoppzeiten, so dass mit Wahrscheinlichkeit
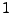
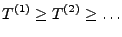 und und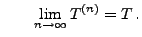 |
(4) |
- Beweis

Korollar 3.2

Sei
![$ T:\Omega\to[0,\infty]$](img1590.png)
eine
beliebige endliche Stoppzeit. Der Prozess
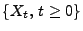
sei
càdlàg und über dem gleichen Wahrscheinlichkeitsraum
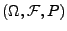
wie
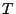
gegeben. Dann gilt
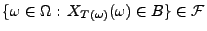
für
jedes
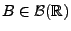
, d.h., die Abbildung
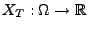
mit
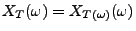 |
(7) |
ist
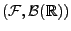
-messbar.
- Beweis





Nächste Seite: Submartingale und Supermartingale; Beispiele
Aufwärts: Martingale
Vorherige Seite: Martingale
Inhalt
Ursa Pantle
2005-07-13
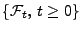 von Teil-
von Teil-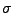 -Algebren
von
-Algebren
von
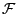 heißt Filtration, wenn
heißt Filtration, wenn
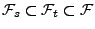 für beliebige
für beliebige 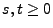 mit
mit
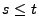 gilt.
gilt.
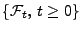 heißt vollständig,
wenn
heißt vollständig,
wenn
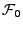 (und damit auch
(und damit auch
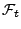 für jedes
für jedes 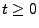 )
sämtliche Nullmengen enthält.
)
sämtliche Nullmengen enthält.
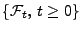 heißt rechtsstetig,
wenn
heißt rechtsstetig,
wenn
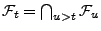 für jedes
für jedes 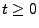 .
.
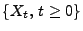 ein stochastischer Prozess über
ein stochastischer Prozess über
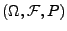 , und für jedes
, und für jedes 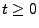 sei
sei
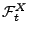 die
kleinste
die
kleinste 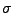 -Algebra, für die
für beliebige
-Algebra, für die
für beliebige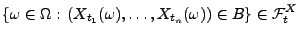
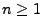 ,
,
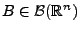 und
und
![$ t_1,\ldots,t_n\in[0,t]$](img1588.png) gilt. Dann heißt
gilt. Dann heißt
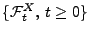 die natürliche Filtration, die von
die natürliche Filtration, die von 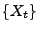 erzeugt wird.
erzeugt wird.
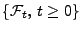 eine beliebige Filtration, und sei
eine beliebige Filtration, und sei
![$ T:\Omega\to[0,\infty]$](img1590.png) eine beliebige Zufallsvariable über
eine beliebige Zufallsvariable über
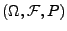 . Man sagt, dass
. Man sagt, dass 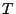 eine Stoppzeit
(bezüglich der Filtration
eine Stoppzeit
(bezüglich der Filtration
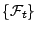 ) ist, wenn
) ist, wenn