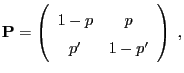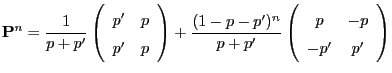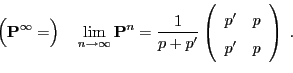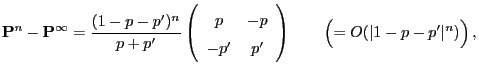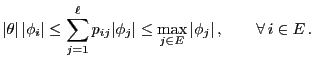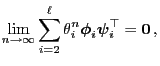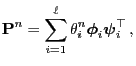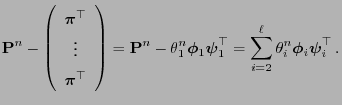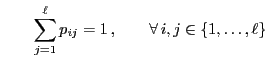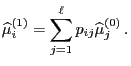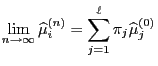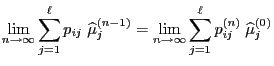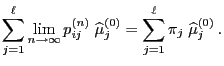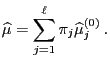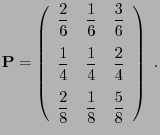Next: Irreducible and Aperiodic Markov
Up: Ergodicity and Stationarity
Previous: Basic Definitions and Quasi-positive
Contents
Estimates for the Rate of Convergence;
Perron-Frobenius-Theorem
- Example
 (Weather Forecast)
(Weather Forecast)
- Let
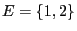 and
and
- In Section 2.2.1 we showed that
- the
 -step transition matrix
-step transition matrix
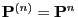 is given by
is given by
- and thus
- Consequently
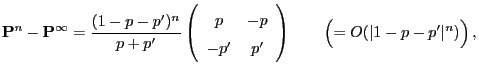 |
(44) |
where
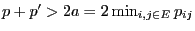 and hence
and hence
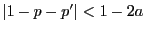 if
if
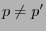 .
.
- Remarks
In general geometric estimates of the form (44) for
the rate of convergence can be derived by means of the following
so-called Perron-Frobenius theorem for quasi-positive
matrices.
Theorem 2.6
- Let
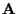 be a quasi-positive
be a quasi-positive
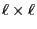 matrix with
eigenvalues
matrix with
eigenvalues
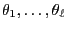 such that
such that
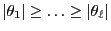 .
.
- Then the following holds:
- (a)
- The eigenvalue
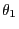 is real and positive.
is real and positive.
- (b)
-
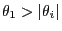 for all
for all
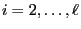 ,
,
- (c)
- The right and left eigenvectors
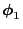 and
and
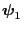 of
of
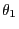 are uniquely determined up to a constant factor and can
be chosen such that all components of
are uniquely determined up to a constant factor and can
be chosen such that all components of
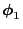 and
and
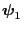 are positive.
are positive.
A proof of Theorem 2.6 can be found in
Chapter 1 of E. Seneta (1981) Non-Negative Matrices and
Markov Chains, Springer, New York.
- Proof
-
- As
 is a stochastic matrix
is a stochastic matrix
- obviously
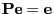 and (41) implies
and (41) implies
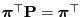 .
.
- Thus
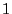 is an eigenvalue of
is an eigenvalue of
 and
and
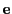 and
and
 are
right and left eigenvectors of this eigenvalue, respectively.
are
right and left eigenvectors of this eigenvalue, respectively.
- Let now be
- Theorem 2.6 now implies
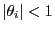 for
for
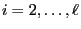 .
.

Corollary 2.3 yields the following geometric
convergence estimate.
Corollary 2.4

Let

be a quasi-positive transition matrix such that all
eigenvalues
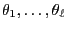
of

are pairwise
distinct. Then
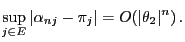 |
(45) |
- Proof
-
- Example
 (Reaching a Consensus)
(Reaching a Consensus)
see C. Hesse (2003) Angewandte Wahrscheinlichkeitstheorie.
Vieweg, Braunschweig, p. 349
- Remarks
-
- For large
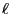 the algebraic solution of the linear equation
system (41) can be difficult.
the algebraic solution of the linear equation
system (41) can be difficult.
- In this case the estimates for the rate of convergence in
(47) become relevant for the practical implementation
of the method to reach a consensus described in (47).
- We consider the following numerical example.
- Let
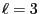 and
and
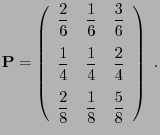 |
(49) |
- The entries of this stochastic matrix imply that the third expert
has a particularly high reputation among his colleagues.
- The solution
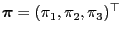 of the corresponding
linear equation system (41) is given by
i.e. the projection
of the corresponding
linear equation system (41) is given by
i.e. the projection
 of the third expert with
the outstanding reputation is most influential.
of the third expert with
the outstanding reputation is most influential.
- The eigenvalues of the transition matrix given in
(49) are
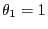 ,
,
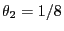 and
and
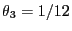 .
.
- The ,,basis'' in the rate of convergence given by
(43) is
whereas Corollary 2.4 yields the following
substantially improved geometric rate of convergence
where
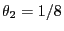 denotes the second largest eigenvalue of the
stochastic matrix
denotes the second largest eigenvalue of the
stochastic matrix
 given by (49).
given by (49).




Next: Irreducible and Aperiodic Markov
Up: Ergodicity and Stationarity
Previous: Basic Definitions and Quasi-positive
Contents
Ursa Pantle
2006-07-20
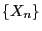 is a Markov chain whose 1-step transition matrix
is a Markov chain whose 1-step transition matrix
 has only strictly positive entries
has only strictly positive entries 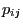 ,
,
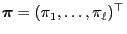 derived in
(40) is given as follows:
derived in
(40) is given as follows:
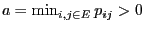 .
.
![]() of the convergence
estimate (43) can be improved.
of the convergence
estimate (43) can be improved.