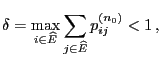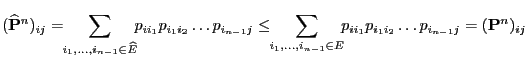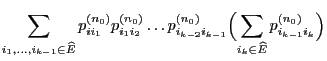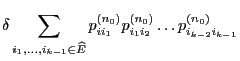Next: Reversibility; Estimates for the
Up: Ergodicity and Stationarity
Previous: Stationary Initial Distributions
Contents
Direct and Iterative Computation Methods
First we show how the stationary initial distribution
 of the
Markov chain
of the
Markov chain 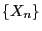 can be computed based on methods from
linear algebra in case the transition matrix
can be computed based on methods from
linear algebra in case the transition matrix
 does not
exhibit a particularly nice structure (but is quasi-positive) and
if the number
does not
exhibit a particularly nice structure (but is quasi-positive) and
if the number 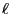 of states is reasonably small.
of states is reasonably small.
- Proof
-
- In order to prove that the matrix
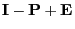 is invertible
we show that the only solution of the equation
is invertible
we show that the only solution of the equation
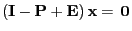 |
(74) |
is given by
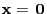 .
.
- As
 satisfies the equation
satisfies the equation
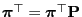 we
obtain
we
obtain
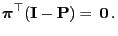 |
(75) |
- Thus (74) implies
i.e.
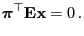 |
(76) |
- On the other hand, clearly
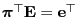 and hence
as a consequence of (76)
and hence
as a consequence of (76)
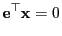 and and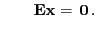 |
(77) |
- Taking into account (74) this implies
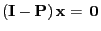 and, equivalently,
and, equivalently,
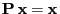 .
.
- Thus, we also have
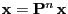 for all
for all 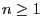 .
.
- Furthermore, Theorem 2.4 implies
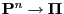 ,
,
- Thus, the matrix
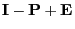 is invertible.
is invertible.
- Finally, (75) implies
and, equivalently,

- Remarks
-
- Proof
-
- Proof
-
- Remarks
-




Next: Reversibility; Estimates for the
Up: Ergodicity and Stationarity
Previous: Stationary Initial Distributions
Contents
Ursa Pantle
2006-07-20
![]()
![]() of the
Markov chain
of the
Markov chain ![]() can be computed based on methods from
linear algebra in case the transition matrix
can be computed based on methods from
linear algebra in case the transition matrix
![]() does not
exhibit a particularly nice structure (but is quasi-positive) and
if the number
does not
exhibit a particularly nice structure (but is quasi-positive) and
if the number ![]() of states is reasonably small.
of states is reasonably small.