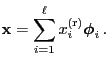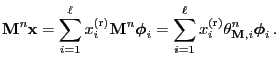Next: Alternative Estimate for the
Up: Reversibility; Estimates for the
Previous: Determining the Rate of
Contents
Multiplicative Reversible Version of the Transition Matrix;
Spectral Representation
At first we will discuss a method enabling us to transform (ergodic)
transition matrices such that the resulting matrix is reversible.
- Definition
 The matrix
The matrix
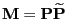 is called the multiplicative reversible version of the transition matrix
is called the multiplicative reversible version of the transition matrix
 .
.
- Remarks
-
This yields the following spectral representation of the
multiplicative reversible version
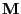 obtained from the
transition matrix
obtained from the
transition matrix
 ; see also the spectral representation
given by formula (30).
; see also the spectral representation
given by formula (30).
Theorem 2.15

For arbitrary
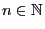
and
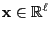
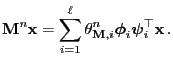 |
(101) |
where
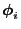
and
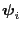
are the right and left
eigenvectors of
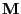
defined in
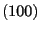
.
- Proof
-




Next: Alternative Estimate for the
Up: Reversibility; Estimates for the
Previous: Determining the Rate of
Contents
Ursa Pantle
2006-07-20
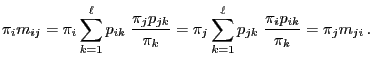
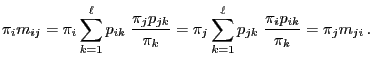
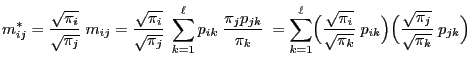
![]() obtained from the
transition matrix
obtained from the
transition matrix
![]() ; see also the spectral representation
given by formula (30).
; see also the spectral representation
given by formula (30).