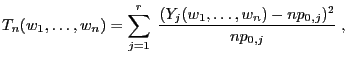- if the generated pseudo-random numbers can be regarded as realizations of uniformly distributed random variables
- and if we may assume the independence of these random variables.
In literature numerous statistical significance tests are discussed in order to investigate characteristics of random number generators; see e.g. G.S. Fishman (1996) Monte Carlo: Concepts, Algorithms and Applications, Springer, New York.
The following test is considered in order to check if the
pseudo-random numbers
![]()
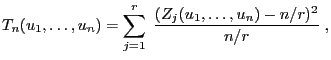
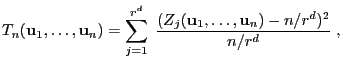
There are a number of other significance tests allowing to evaluate the quality of random number generators. In particular it can be verified
The significance test that will be constructed is based on the
following property of the runs
![]() .
.
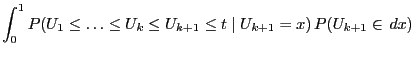 |
|||
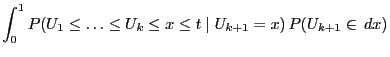 |
|||
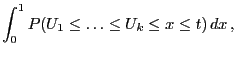 |
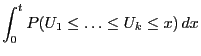 |
|||
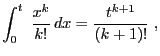 |
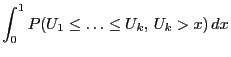 |
|||
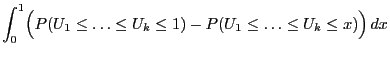 |
|||
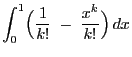 |
|||
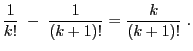 |
![$\displaystyle p_{0,j}=\sum\limits
_{k\in\mathbb{N}\cap(a_j,b_j]}\frac{k}{(k+1)!}\,,\qquad j=1,\ldots,r
$](img1222.png)