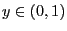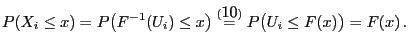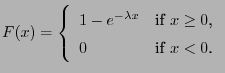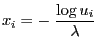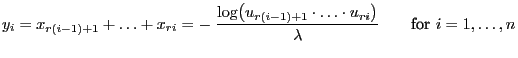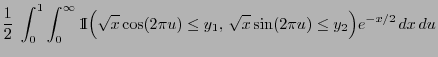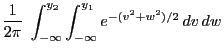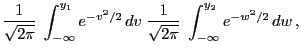Next: Transformation Algorithms for Discrete
Up: Transformation of Uniformly Distributed
Previous: Transformation of Uniformly Distributed
Contents
Inversion Method
- The following property of the generalized inverse can be used as a
basis for the generation of pseudo-random numbers
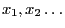 that can be regarded as realizations of random variables
that can be regarded as realizations of random variables
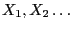 whose distribution function
whose distribution function
![$ F:\mathbb{R}\to[0,1]$](img1230.png) is an
arbitrary monotonically nondecreasing and right-continuous
function such that
is an
arbitrary monotonically nondecreasing and right-continuous
function such that
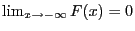 and
and
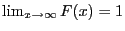 .
.
- Recall the following auxiliary result.
Theorem 3.4
- Let
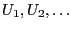 be a sequence of independent and uniformly
distributed random variables on
be a sequence of independent and uniformly
distributed random variables on ![$ (0,1]$](img165.png) and let
and let
![$ F:\mathbb{R}\to[0,1]$](img1230.png) be a
distribution function.
be a
distribution function.
- Then the random variables
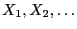 where
where
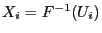 for
for
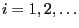 are independent and their distribution function
is given by
are independent and their distribution function
is given by 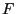 .
.
- Proof
-
- Examples
-
- In the following we discuss some examples illustrating
- how Theorem 3.4 can be used in order to generate
pseudo-random numbers
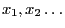
- that can be regarded as realizations of independent random variables
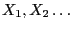 with a given distribution function
with a given distribution function
![$ F:\mathbb{R}\to[0,1]$](img1230.png) .
.
- These numbers are also referred to as
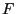 -distributed
pseudo-random numbers
-distributed
pseudo-random numbers
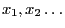 ,
,
- in spite of the fact that the empirical distribution function
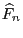 of the sample
of the sample
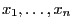
- is only an approximation of
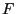 for large
for large  .
.
- Note that Theorem 3.4 can only be applied directly if
- the generalized inverse
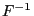 of
of 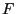 is given explicitly (i.e. by
an analytical formula).
is given explicitly (i.e. by
an analytical formula).
- Unfortunately, this situation is merely an exception.
- Exponential distribution
- Let
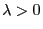 and
and
![$ F:\mathbb{R}\to[0,1]$](img1230.png) be the distribution function
of the Exp
be the distribution function
of the Exp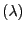 -distribution, i.e.
-distribution, i.e.
- Then
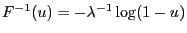 for all
for all ![$ u\in(0,1]$](img1250.png) .
.
- By Theorem 3.4,
- Erlang distribution
- Let
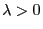 ,
,
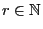 and let
and let
![$ F:\mathbb{R}\to[0,1]$](img1230.png) be the
distribution function of the Erlang distribution, i.e., of the
be the
distribution function of the Erlang distribution, i.e., of the
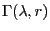 -distribution where
-distribution where
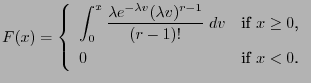 |
(11) |
- Then the generalized inverse
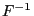 of
of  cannot be determined
explicitly and therefore Theorem 3.4 cannot be
applied directly.
cannot be determined
explicitly and therefore Theorem 3.4 cannot be
applied directly.
- However, in Section 1.3.1 of the course ,,Statistik I'' we showed
that
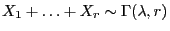 if the random variables
if the random variables
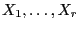 are independent and Exp
are independent and Exp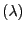 -distributed.
-distributed.
- By Theorem 3.4
- Normal distribution




Next: Transformation Algorithms for Discrete
Up: Transformation of Uniformly Distributed
Previous: Transformation of Uniformly Distributed
Contents
Ursa Pantle
2006-07-20
![$ F:\mathbb{R}\to[0,1]$](img1230.png) be an arbitrary distribution function. Then the
function
be an arbitrary distribution function. Then the
function
![$ F^{-1}:(0,1]\to\mathbb{R}\cup\{\infty\}$](img1233.png) where
where
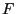 .
.
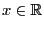 and
and