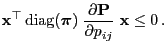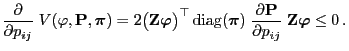Next: Coupling Algorithms; Perfect MCMC
Up: Error Analysis for MCMC
Previous: MCMC Estimators; Bias and
Contents
Asymptotic Variance of Estimation; Mean Squared Error
For the statistical model introduced in Section 3.4.2
we now investigate the asymptotic behavior of the variance
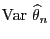 if
if
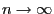 .
.
Theorem 3.19

Define
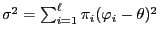
and let
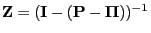
be the fundamental matrix of

defined by
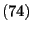
. Then
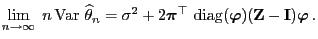 |
(78) |
- Proof
-
- Clearly,
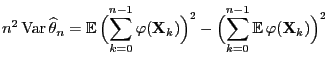 |
(79) |
and thus
- This representation will now be used to show (78) for
the case
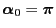 .
.
- In this case we observe
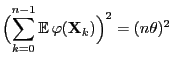
and
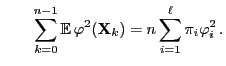
- Furthermore, by the stationarity of the Markov chain
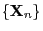 ,
,
where
and
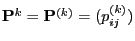 denotes the matrix of
the
denotes the matrix of
the 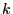 -step transition probabilities.
-step transition probabilities.
- A combination of the results above yields
- where the second equality is due to the identity
- Taking into account the representation formula (76)
for
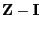 this implies (78).
this implies (78).
- It is left to show that (78) is also true for an
arbitrary initial distribution
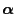 .
.
- Remarks
-
In order to investigate this problem more deeply we introduce the
following notation: Let
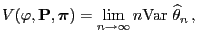
where
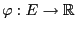 is an arbitrary function and
is an arbitrary function and
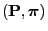 is an arbitrary reversible pair.
is an arbitrary reversible pair.
- Proof
-
- Let
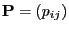 be a transition matrix such that the pair
be a transition matrix such that the pair
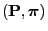 is reversible. It suffices to show that
is reversible. It suffices to show that
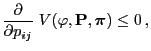 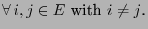 |
(83) |
- By Theorem 3.19,
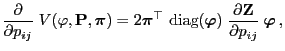 |
(84) |
where
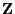 denotes the fundamental matrix of
denotes the fundamental matrix of
 introduced
by (74).
introduced
by (74).
- On the other hand, as
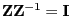 , we get that
and thus
, we get that
and thus
- Taking into account (84) this implies
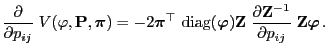 |
(85) |
- As the pair
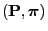 is reversible, by the representation
formula (75) for the fundamental matrix
is reversible, by the representation
formula (75) for the fundamental matrix
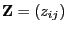 that was derived in Lemma 3.3 we
obtain for arbitrary
that was derived in Lemma 3.3 we
obtain for arbitrary 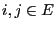
- This implies
- Thus, by (85),
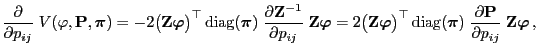 |
(86) |
where the last equality is due to the fact that
which is an immediate consequence of the definition
(74) of
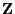 .
.
- As
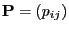 is a stochastic matrix and
is a stochastic matrix and
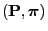 is
reversible
is
reversible
- This completes the proof of (83).

- Remarks
 As a particular consequence of Theorem 3.20 we get
that
As a particular consequence of Theorem 3.20 we get
that
- the simulation matrix
 of the Metropolis algorithm (i.e.
if we consider equality in (50) ) minimizes the
asymptotic variance
of the Metropolis algorithm (i.e.
if we consider equality in (50) ) minimizes the
asymptotic variance
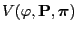
- within the class of all Metropolis-Hastings algorithms having an
arbitrary but fixed ,,potential transition matrix''
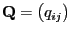 .
.




Next: Coupling Algorithms; Perfect MCMC
Up: Error Analysis for MCMC
Previous: MCMC Estimators; Bias and
Contents
Ursa Pantle
2006-07-20
![]() if
if
![]() .
.
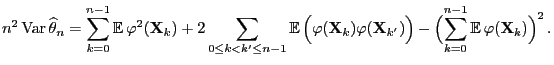
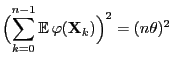 and
and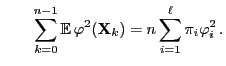
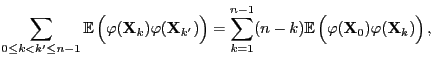
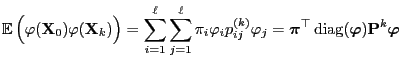
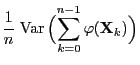
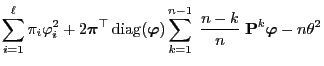
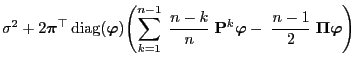
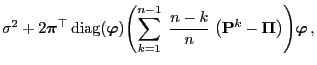
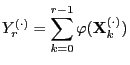 und
und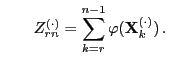
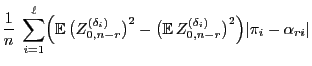
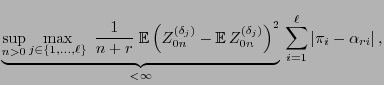
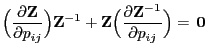
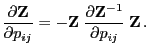
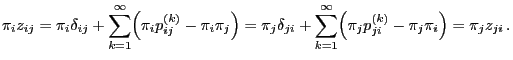
![\begin{displaymath}
\Bigl({\,{\rm diag}}({\boldsymbol{\pi}}) \;\frac{\partial {\...
...rime)=(j,i)$,}\\ [3\jot]
0\,, &\mbox{else}
\end{array}\right.
\end{displaymath}](img1926.png)