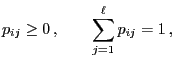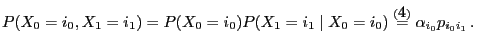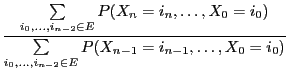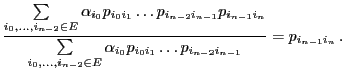- The model is based on the (finite) set of all possible states called
the state space of the Markov chain. W.l.o.g. the state space
can be identified with the set
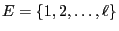 where
where
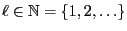 is an arbitrary but fixed natural
number.
is an arbitrary but fixed natural
number.
- For each
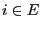 , let
, let 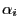 be the probability of the
system or object to be in state
be the probability of the
system or object to be in state 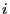 at time
at time 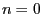 , where it is
assumed that
, where it is
assumed that
The vector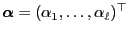 of the
probabilities
of the
probabilities
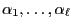 defines the initial
distribution of the Markov chain.
defines the initial
distribution of the Markov chain.
- Furthermore, for each pair
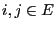 we consider the (conditional)
probability
we consider the (conditional)
probability
![$ p_{ij}\in[0,1]$](img26.png) for the transition of the object or
system from state
for the transition of the object or
system from state 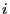 to
to 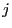 within one time step.
within one time step.
- The
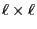 matrix
matrix
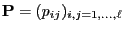 of the transition probabilities
of the transition probabilities 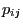 where
where
is called one-step transition matrix of the Markov chain.
![$\displaystyle \alpha_i\in[0,1]\,,\qquad\sum\limits_{i=1}^\ell \alpha_i=1\,.$](img22.png)