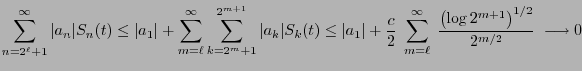Vollständige Orthonormalsysteme im $L_2$; Haar-Funktionen und Schauder-Funktionen

Wir betrachten zunächst den Fall, dass $I=[0,1]$ das Einheitsintervall ist. Dabei benötigen wir zur Konstruktion von Wiener-Prozessen in $[0,1]$ einige analytische Hilfsmittel.

• Insbesondere betrachten wir den Hilbert-Raum $L_2=L_2([0,1])$
  • aller auf dem Einheitsintervall $I=[0,1]$ definierten (Borel-messbaren) Funktionen $f:[0,1]\to\mathbb{R}$, die bezüglich des Lebesgue-Maßes quadratisch integrierbar sind, d.h., für die $\int_0^1 f^2(s) {\rm d}s<\infty$ gilt.
  • Für beliebige $f,g\in L_2$ sei $(f,g)=\int_0^1 f(s)g(s) {\rm d} s$ das zugehörige Skalarprodukt.
• Eine Folge $\{f_n, n\ge 1\}$ von Funktionen $f_n\in L_2$ wird ein vollständiges Orthonormalsystem in $L_2$ genannt,
  • wenn $(f_n,f_n)=1$ und $(f_n,f_m)=0$ für beliebige $n\not= m$ und
  • wenn für jedes $g\in L_2$ die Gültigkeit von $(g,f_n)=0$ für jedes $n\ge 1$ impliziert, dass $g(s)=0$ für fast jedes $s\in[0,1]$.

Die Konstruktion von Wiener-Prozessen in $I=[0,1]$ beruht auf der Idee,

• ein speziell gewähltes Orthonormalsystem $\{H_n, n\ge 1\}$ in $L_2$ (die sogenannten Haar-Funktionen) sowie
• eine Folge $\{Y_n, n\ge 1\}$ von unabhängigen und N$(0,1)$-verteilten Zufallsvariablen über einem Wahrscheinlichkeitsraum $(\Omega,\mathcal{F},P)$ zu betrachten und zu zeigen, dass
• der stochastische Prozess $\{X_t, t\in [0,1]\}$ mit

  $$X_t=\sum_{n=1}^\infty Y_n\int_0^t H_n(s) {\rm d}s\qquad\forall t\in[0,1]$$ (1)

  
  
  über einer gewissen Einschränkung des Wahrscheinlichkeitsraumes $(\Omega,\mathcal{F},P)$ wohldefiniert ist und den Bedingungen eines Wiener-Prozesses in $[0,1]$ genügt.

Definition

$\;$ Die durch den Ansatz

$$H_1(s) = 1 \mbox{für jedes $s\in[0,1]$,}$$ (2)

$$H_{2^{m+1}}(s) = \left\{\begin{array}{cl} \displaystyle 2^{\frac{m}{2}} &\mbox{für... ...ac{2^{m+1}-1}{2^{m+1}}\;, 1\Bigr] ,$}\\ 0 & \mbox{sonst,} \end{array}\right.$$ (3)

$$H_{2^m+k}(s) = \left\{\begin{array}{cl} \displaystyle 2^{\frac{m}{2}} &\mbox{für... ...1}{2^{m+1}}\;,\;\frac{k}{2^m}\Bigr) ,$}\\ 0 & \mbox{sonst} \end{array}\right.$$ (4)

für $k=1,2,\ldots,2^m-1$ und $m=0,1,2,\ldots$ gegebenen Funktionen $H_n:[0,1]\to\mathbb{R}$ heißen Haar-Funktionen, vgl. Abb. 7 und 8.

Abbildung 7: Haar-Funktionen $H_2$ und $H_3$

[width=6cm]Bilder/Haar2.eps [width=6cm]Bilder/Haar3.eps

Abbildung 8: Haar-Funktion $H_4$

[width=6cm]Bilder/Haar4.eps

Lemma 2.5   $\;$ Die in $(\ref{def.haa.one})$ - $(\ref{def.haa.the})$ definierten Haar-Funktionen $H_n:[0,1]\to\mathbb{R}$ mit $n=1,2,\ldots$ bilden ein vollständiges Orthonormalsystem in $L_2$. Insbesondere gilt die sogenannte Parseval-Identität

$$(f,g)=\sum_{n=1}^\infty (f,H_n) (g,H_n)\qquad\forall f,g\in L_2 .$$ (5)

Beweis

 

• Unmittelbar aus der Definition der Haar-Funktionen folgt, dass $(H_n,H_n)=1$ und $(H_n,H_m)=0$ für beliebige $n,m\ge 1$ mit $n\not= m$ gilt.
• Außerdem kann man leicht zeigen, dass das Orthonormalsystem $\{H_n, n\ge 1\}$ vollständig in $L_2$ ist.
  • Sei $g\in L_2$ eine quadratisch integrierbare Funktion mit
    $$\int_0^1 g(s) H_n(s) {\rm d}s=0\qquad\forall n\ge 1 .$$

  • Hieraus folgt, dass $\int_{k/2^m}^{(k+1)/2^m}g(s) {\rm d}s=0$ für beliebige $m=0,1,\ldots$ und $k=1,\ldots,2^m-1$.
  • Insbesondere gilt also für die Funktion $G:[0,1]\to\mathbb{R}$ mit $G(t)=\int_0^t g(s) {\rm d} s$, dass $G(k/2^m)=0$ für beliebige $m=0,1,\ldots$ und $k=1,\ldots,2^m-1$.
  • Weil $G$ eine stetige Funktion ist, folgt hieraus, dass $G(t)=0$ für jedes $t\in[0,1]$ und somit $g(s)=0$ für fast jedes $s\in[0,1]$.
• Die Gültigkeit von (5) ergibt sich aus der Vollständigkeit des Orthonormalsystems $\{H_n, n\ge 1\}$, vgl. beispielsweise Satz 5.3.6 in W. Arendt (2002) Funktionalanalysis (Vorlesungskript, Universität Ulm) bzw. Satz V.4.9 in D. Werner (1997) Funktionalanalysis (Springer, Berlin).
  
  $\Box$

Abbildung 9: Schauder-Funktionen $S_1$ und $S_2$

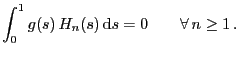
[width=6cm]Bilder/Schauder1.eps [width=6cm]Bilder/Schauder2.eps

Abbildung 10: Schauder-Funktionen $S_3$ und $S_4$

[width=6cm]Bilder/Schauder3.eps[width=6cm]Bilder/Schauder4.eps

Lemma 2.6   $\;$ Für jedes $n=1,2,\ldots$ sei die Funktion $S_n:[0,1]\to\mathbb{R}$ gegeben durch

$$S_n(t)=\int_0^t H_n(s) {\rm d}s\qquad\forall t\in[0,1] .$$ (6)

Die in $(\ref{def.sch.fun})$ definierten Funktionen $S_1,S_2,\ldots:[0,1]\to\mathbb{R}$, die Schauder-Funktionen genannt werden, besitzen die folgenden Eigenschaften:

$1$

Für beliebige $n\ge 1$ und $t\in[0,1]$ gilt $S_n(t)\ge 0$.

$2$

Für beliebige $m=1,2,\ldots$ und $t\in[0,1]$ gilt die Ungleichung

$$\sum_{k=1}^{2^m}S_{2^m+k}(t)\le \frac{1}{2}\;2^{-m/2}\;.$$ (7)

$3$

Sei $a_1,a_2,\ldots\in\mathbb{R}$ eine beliebige Folge reeller Zahlen mit $a_n={\rm O}((\log n)^{1/2})$ für $n\to\infty$. Dann konvergiert die Reihe $\sum_{n=1}^\infty a_n S_n(t)$ absolut und gleichmäßig in $t\in[0,1]$.

Beweis

 

• Die Tatsache, dass die Schauder-Funktionen $S_n$ nur nichtnegative Werte haben, ergibt sich unmittelbar aus den Definitionsgleichungen (2)-(4) bzw. (6), vgl. auch Abb. 9 und 10.
• Um die Gültigkeit der Ungleichung (7) zu zeigen, genügt es zu beachten, dass die Funktionen $S_{2^m+k}$ für $k=1,\ldots,2^m$ disjunkte Träger haben und dass
  $$S_{2^m+k}(t)\le S_{2^m+k}\Bigl(\frac{2k-1}{2^{m+1}}\Bigr)= 2^{m/2}\;\frac{1}{2^{m+1}}\;=\;\frac{1}{2}\;2^{-m/2}\qquad\forall t\in[0,1] .$$

• Sei nun $c>0$ eine Konstante, so dass $\vert a_n\vert\le c (\log n)^{1/2}$ für jedes $n\ge 1$.
  • Dann ergibt sich aus (7), dass für $\ell\to\infty$
    $$\sum_{n=2^\ell+1}^\infty \vert a_n\vert S_n(t)\le \vert a_1\vert+... ...ell}^\infty\;\frac{\bigl(\log 2^{m+1}\bigr)^{1/2}}{2^{m/2}}\;\longrightarrow 0$$
    gleichmäßig in $t\in[0,1]$,
  • weil $m+1<c^\prime 2^{\varepsilon m}$ für jedes $m\ge 0$ und für gewisse Konstanten $c^\prime<\infty$ bzw. $\varepsilon<1$
  • und weil somit
    $$\sum_{m=\ell}^\infty\;\frac{\bigl(\log 2^{m+1}\bigr)^{1/2}}{2^{m/... ...^\infty\;\Bigl(\frac{1}{2^{(1-\varepsilon)m}}\Bigr)^{1/2} \longrightarrow 0 .$$

  • Damit ist auch die dritte Teilaussage bewiesen.
    
    $\Box$