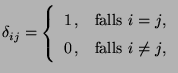Next: Schätzung des Vektors der
Up: Methode der kleinsten Quadrate
Previous: Methode der kleinsten Quadrate
Contents
Grundlagen der Matrix-Algebra
Wir erinnern zunächst an einige grundlegende Begriffe und
Ergebnisse der Matrix-Algebra, die bei der Minimierung des
mittleren quadratischen Fehlers
 in
(6) nützlich sind.
in
(6) nützlich sind.
Lemma 3.1
Sei
eine
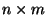
Matrix mit
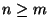
und
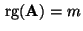
. Dann gilt auch
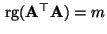
, wobei
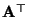
die transponierte
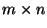
Matrix bezeichnet, die
sich durch Vertauschung der Zeilen und Spalten von
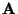
ergibt.
- Beweis
-
- Es ist klar, daß der Rang
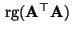 der
der 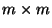 Matrix
Matrix
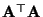 nicht größer als
nicht größer als 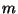 sein kann.
sein kann.
- Wir nehmen nun an, daß
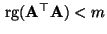 . Dann gibt es
einen Vektor
. Dann gibt es
einen Vektor
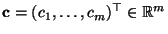 , so daß
, so daß
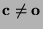 und
und
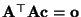 .
.
- Hieraus folgt, daß auch
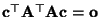 bzw.
bzw.
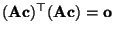 , d.h.
, d.h.
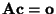 .
.
- Dies ist jedoch ein Widerspruch zu der Voraussetzung, daß
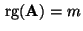 .
.

- Definition
-
- Beweis
-
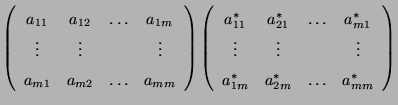
- Definition
 Sei
Sei
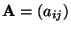 eine beliebige
eine beliebige 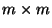 Matrix. Die Determinante
Matrix. Die Determinante
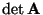 von
von
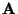 ist dann gegeben durch
ist dann gegeben durch
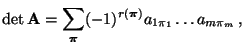 |
(8) |
wobei sich die Summation über alle 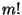 Permutationen
Permutationen
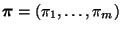 der natürlichen Zahlen
der natürlichen Zahlen
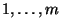 erstreckt und
erstreckt und
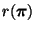 die Anzahl der Zahlenpaare in
die Anzahl der Zahlenpaare in
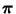 ist, die sich nicht in der natürlichen Ordnung befinden.
ist, die sich nicht in der natürlichen Ordnung befinden.
- Beachte
-
- Unmittelbar aus der Definitionsgleichung (8) der
Determinante ergibt sich, daß
- die Determinante der Einheitsmatrix
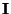 gleich
gleich 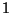 ist,
ist,
- das Vorzeichen von
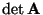 sich ändert, wenn zwei Zeilen oder
zwei Spalten von
sich ändert, wenn zwei Zeilen oder
zwei Spalten von
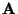 miteinander vertauscht werden,
miteinander vertauscht werden,
-
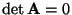 , wenn
, wenn
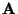 zwei identische Zeilen oder zwei
identische Spalten hat.
zwei identische Zeilen oder zwei
identische Spalten hat.
- Außerdem gelten die folgenden rekursiven Darstellungsformeln, die
wir hier ohne Beweis angeben.
- Beachte
-
- Aus (9) und (10) ergibt sich
die Gültigkeit von
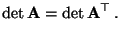 |
(11) |
- Außerdem ist die folgende Faktorisierungseigenschaft der
Determinante von Matrix-Produkten nützlich, die wir ebenfalls ohne
Beweis angeben.
Lemma 3.4

Seien
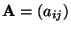
und
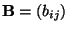
beliebige
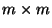
Matrizen. Dann gilt
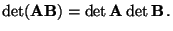 |
(12) |
Schließlich erwähnen wir (zum Teil ohne Beweis) die folgende Charakterisierung der Regularität einer quadratischen Matrix
mit Hilfe von Rang bzw. Determinante.
- Beachte
-
- Die Implikation
 in
Theorem 3.1 ergibt sich unmittelbar aus der in
Lemma 3.4 erwähnten Faktorisierungseigenschaft der
Determinante von Matrix-Produkten , denn aus
ergibt sich, daß
in
Theorem 3.1 ergibt sich unmittelbar aus der in
Lemma 3.4 erwähnten Faktorisierungseigenschaft der
Determinante von Matrix-Produkten , denn aus
ergibt sich, daß
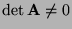 .
.
- Umgekehrt ergibt sich die Implikation
 auf die folgende Weise aus den in
Lemma 3.3 angegebenen rekursiven Darstellungsformeln
der Determinante.
auf die folgende Weise aus den in
Lemma 3.3 angegebenen rekursiven Darstellungsformeln
der Determinante.
- In diesem Zusammenhang ist der folgende Begriff nützlich: Die
Matrix
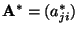 mit
mit
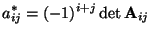 |
(13) |
heißt die zu
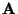 adjungierte Matrix.
adjungierte Matrix.
- Aus den Rekursionsformeln (9) bzw.
(10) und aus der Tatsache, daß die Determinante
von Matrizen mit zwei identischen Zeilen oder zwei identischen
Spalten gleich Null ist, ergibt sich nun, daß
bzw.
- Hieraus folgt, daß
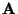 regulär ist, falls
regulär ist, falls
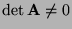 ,
und daß in diesem Fall
,
und daß in diesem Fall
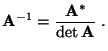 |
(14) |




Next: Schätzung des Vektors der
Up: Methode der kleinsten Quadrate
Previous: Methode der kleinsten Quadrate
Contents
Ursa Pantle
2003-03-10
![]() in
(6) nützlich sind.
in
(6) nützlich sind.