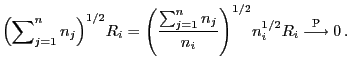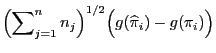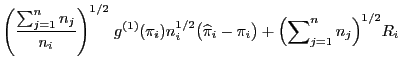Nächste Seite: Asymptotische Normalverteiltheit des KQ-Schätzers
Aufwärts: Gewichteter KQ-Schätzer bei kategorialer
Vorherige Seite: Gewichteter KQ-Schätzer bei kategorialer
Inhalt
Schätzung des Erwartungswertvektors
Zur Erinnerung (vgl. Abschnitt 4.2.2):  Im
binären kategorialen Regressionsmodell sind die
Stichprobenvariablen
Im
binären kategorialen Regressionsmodell sind die
Stichprobenvariablen
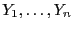 Bernoulli-verteilt, d.h.,
sie können nur die Werte 0 bzw.
Bernoulli-verteilt, d.h.,
sie können nur die Werte 0 bzw. 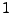 mit positiver
Wahrscheinlichkeit annehmen.
mit positiver
Wahrscheinlichkeit annehmen.
Man kann sich leicht überlegen, dass der Schätzer
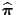 erwartungstreu für
erwartungstreu für
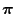 ist und dass seine Kovarianzmatrix
ist und dass seine Kovarianzmatrix
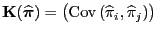 die folgende Form besitzt.
die folgende Form besitzt.
- Beweis
- Die Behauptung ergibt sich unmittelbar aus der
Tatsache, dass die Zufallsvariablen
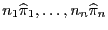 unabhängig und
binomialverteilt sind mit
unabhängig und
binomialverteilt sind mit
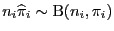 für jedes
für jedes
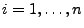 .
.

Außerdem ergibt sich aus dem folgenden zentralen
Grenzwertsatz, dass der Schätzer
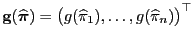 asymptotisch normalverteilt ist.
asymptotisch normalverteilt ist.
Theorem 4.3

Wenn
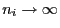
für jedes
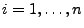
,
so dass
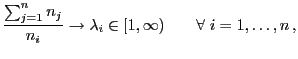 |
(55) |
dann gilt
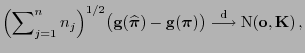 |
(56) |
wobei
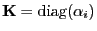 und und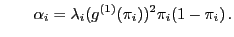 |
(57) |
- Beweis
-




Nächste Seite: Asymptotische Normalverteiltheit des KQ-Schätzers
Aufwärts: Gewichteter KQ-Schätzer bei kategorialer
Vorherige Seite: Gewichteter KQ-Schätzer bei kategorialer
Inhalt
Hendrik Schmidt
2006-02-27
![]() Im
binären kategorialen Regressionsmodell sind die
Stichprobenvariablen
Im
binären kategorialen Regressionsmodell sind die
Stichprobenvariablen
![]() Bernoulli-verteilt, d.h.,
sie können nur die Werte 0 bzw.
Bernoulli-verteilt, d.h.,
sie können nur die Werte 0 bzw. ![]() mit positiver
Wahrscheinlichkeit annehmen.
mit positiver
Wahrscheinlichkeit annehmen.
![]() erwartungstreu für
erwartungstreu für
![]() ist und dass seine Kovarianzmatrix
ist und dass seine Kovarianzmatrix
![]() die folgende Form besitzt.
die folgende Form besitzt.
![]() asymptotisch normalverteilt ist.
asymptotisch normalverteilt ist.