Stack Usage for Function Calls

A stack is a data structure that supports two operations:

• Push: Adds data onto the stack.

• Pop: Removes data (from the top) from the stack.

This data structure is used to manage the lifetime of local variables. Later on, we'll see that this data structure is also used to keep track of where in the program a function should return to.

The code for using this data structure is generated by the compiler and is included in the executable program. In the Bottom-Up sessions of these events, we will write this code ourselves in assembly and understand more precisely what the compiler generates for us. Here, the aim is to understand what this code does. We use the example program depicted on the right for this purpose.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

@ <stdio.hdr>                                                                    
                                                                                 
fn bar(n: int)                                                                   
{                                                                                
    printf("bar entered: n = %d\n", n);                                          
}                                                                                
                                                                                 
fn foo(n: int)                                                                   
{                                                                                
    printf("foo entered: n = %d\n", n);                                          
    bar(n - 1);                                                                  
    printf("foo leaving: n = %d\n", n);                                          
}                                                                                
                                                                                 
fn main()                                                                        
{                                                                                
    foo(3);                                                                      
}                                                                                

Task

• Translate and execute the program ex5.abc. Go through the program line by line to understand which output is generated in each line. For example, realize that the local variable n in the foo function still exists and has an unchanged value even after the bar function call. Also, understand that the bar function also has a variable n, but it is not the same variable as in the foo function.

• The following figure illustrates how a stack is used to manage function calls:

  

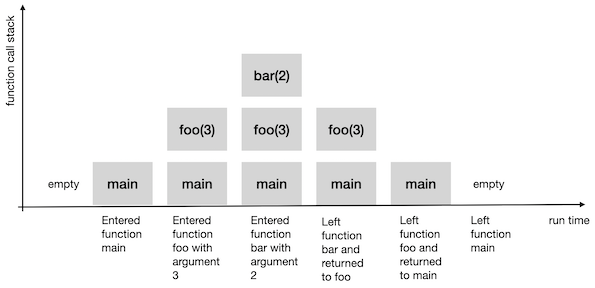
  A box is created with the relevant data for each function call. This relevant data includes the local variables (including function arguments) and, as mentioned above, the return address. These boxes are stacked:

  • The stack is initially empty at the start of the program.

  • When the main function is entered, a box is created and pushed onto the stack.

  • When the foo function with the argument 3 is called in main, a new box is created and pushed onto the stack.

  • When the bar function with the argument 2 is called in foo, a new box is created and pushed onto the stack.

  • When bar exits, the topmost box is removed. When the program execution continues in the foo function, the topmost box contains the state before the function call.

  • And so on.

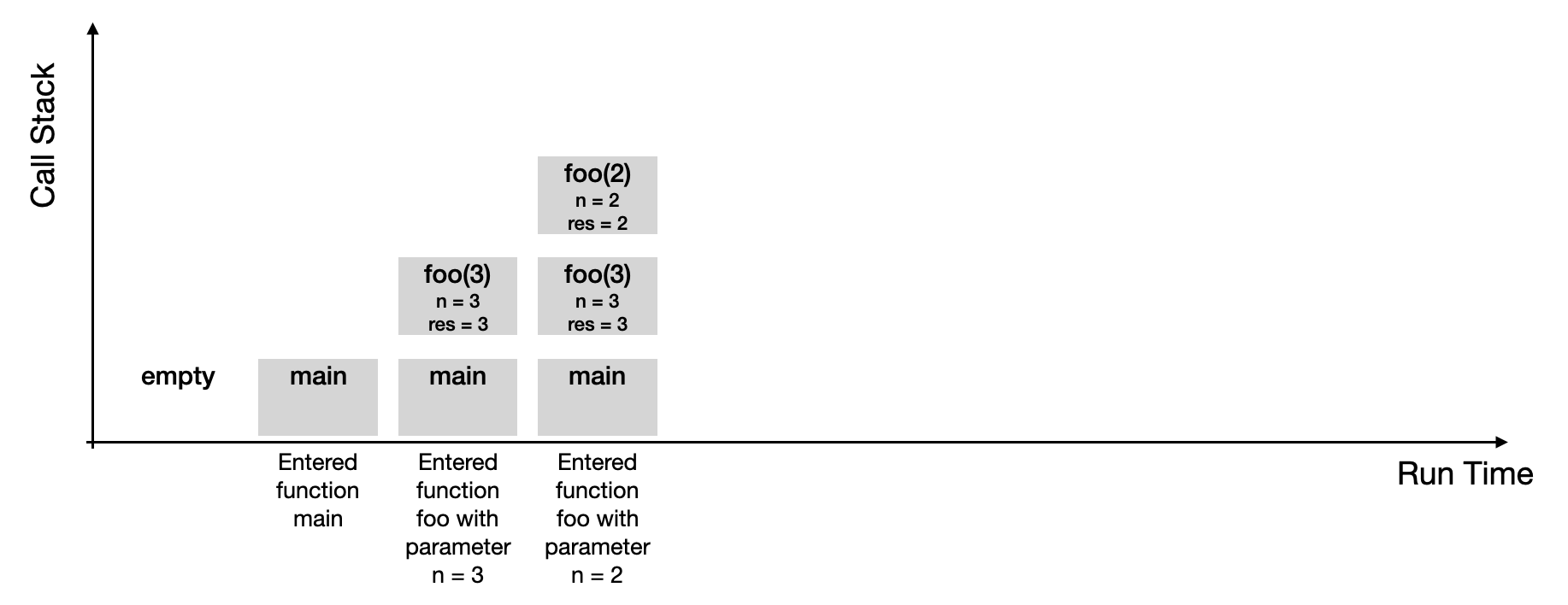
With such diagrams, you can also illustrate the use of the stack for recursive function calls. Do this for program ex6.abc below. Include the values of the local variables in the boxes. Below is an unfinished diagram showing this for the first few function calls.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

@ <stdio.hdr>

fn foo(n: int): int
{
    local res: int = n;

    if (n > 1) {
        res += foo(n - 1);
    }
    return res;
}

fn main()
{
    printf("foo(%d) = %d\n", 3, foo(3));
}

Unfinished diagram

Complete this diagram: