Ute Hahn

Institute of Mathematics (Chair of Stochastics and its Applications)
University of Augsburg

86135 Augsburg
Germany

email: ute.hahn [at] math.uni-augsburg [dot] de
abstract:

Scale invariant summary statistics for stationary and inhomogeneous point processes

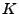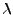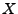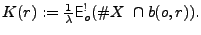
Second order statistics for stationary point processes in their traditional form are scale dependent. An example is Ripley's $ K$-function, which gives the expected number of points in a ball around the typical point, divided by the intensity $ \lambda$ of the process $ X$, in terms of the reduced Palm expectation this is written as $ K(r):=\frac{1}{\lambda}{\mathsf{E}^!_o}(\char93 X\ \cap b(o,r)).$

The 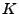$ K$-function of to two non Poisson point processes that differ only by a scale factor is different. On the contrary, the 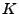$ K$-function is invariant to uniform independent thinning, a fact that has been used by Baddeley et al. (2000) for a generalization to inhomogeneous point processes that result from location dependent thinning. Another way to analyse inhomogeneous point patterns is to assume that they result from a transformation of a homogeneous point process, as in Nielsen and Jensen (2004) and Fleischer et al. (2006), and to reconstruct the original process.

Both methods are not very appropriate in the case of an inhomogeneous pattern which consists of regions that look locally like scaled versions of the same process. Suitable statistics are scale invariant, that is, they coincide for point processes that can be transformed into each other by uniform scaling. We will therefore introduce scale invariant renormalized variants of the known second order statistics. For example, a scale invariant version of the 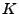$ K$ function is given by 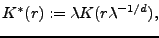$ K^*(r):=\lambda K(r\lambda^{-1/d}),$ which means that $ K^*(r):={\mathsf{E}^!_o}(\char93 X\cap b(o,r/\sqrt[d]{\lambda})).$

The renormalized second order statistics generalize in a natural way to a form for inhomogeneous point processes obtained by local scaling. This is achieved by redefining the way inter-point distances are measured. Given the intensity function 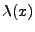$ \lambda(x)$ of the process, the 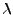$ \lambda$-scaled distance between two point 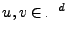$ u,v\in\mathbbm R^d$ shall be defined as $ d_\lambda(u,v):=\int_{[u,v]}\lambda(x)^{1/d} d x$, where integration is along the segment $ u,v$. 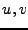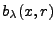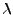This includes redefining the ball $ b_\lambda(x,r)$ as the set of all points with $ \lambda$-scaled distance less than 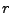$ r$ to the center 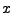$ x$. With this definition, the scale invariant 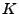$ K$-function reads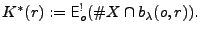 $ K^*(r):={\mathsf{E}^!_o}(\char93 X\cap b_\lambda(o,r)).$

It is not always clear which method is the best for a given inhomogeneous point pattern, since most often the genesis of the pattern can not be uniquely ascribed to a thinning, transformation or local scaling. We will discuss criteria that help to decide which statistics will give the best characterization in this case.

References:

Baddeley, A.J., Moeller, J., Waagepetersen, R. (2000). Non- and semi-parametric estimation of interaction in inhomogeneous point patterns. Statistica Neerlandica, 54, 329-350.

Fleischer, F., Beil, M., Kazda, M., and Schmidt, V. (2006). Analysis of spatial point patterns in microscopic and macroscopic biological image data. Pages 235-260 in Baddeley, A., Gregori, P., Mateu, J., Stoica, R., and Stoyan, D. (editors): Case Studies in Spatial Point Process Modeling, volume 185 of Lecture Notes in Statistics, New York. Springer.

Nielsen, L. S. and Jensen, E. B. V. (2004). Statistical inference for transformation inhomogeneous point processes. Scandinavian Journal of Statistics, 31(1):131-142.
Download presentation: PDF format