


Next: Statistical Analysis of Boolean
Up: The Boolean Model
Previous: The Boolean Model
Let 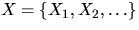 be a homogeneous Poisson process with
intensity
be a homogeneous Poisson process with
intensity 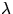 and let
and let 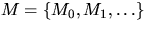 be a sequence
of independent and identically distributed random compact sets
that are independent of the Poisson process X. The union
be a sequence
of independent and identically distributed random compact sets
that are independent of the Poisson process X. The union
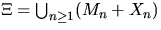 of all shifted sets is called a Boolean model;
see e.g. Hall (1988),
Molchanov (1997), Stoyan et al. (1995),
Weil (1988, 1995).
The points Xi are sometimes called germs and the random set M0
is said to be the `typical grain` of the Boolean model
of all shifted sets is called a Boolean model;
see e.g. Hall (1988),
Molchanov (1997), Stoyan et al. (1995),
Weil (1988, 1995).
The points Xi are sometimes called germs and the random set M0
is said to be the `typical grain` of the Boolean model 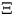 (also
called Poisson germ-grain model).
A realization of a Boolean model where the sets Mn are
discs with uniformly distributed radii Rn in a certain
interval is given in Figure 6.
(also
called Poisson germ-grain model).
A realization of a Boolean model where the sets Mn are
discs with uniformly distributed radii Rn in a certain
interval is given in Figure 6.
Figure 6:
Boolean model
 |
An important characteristic of the Boolean model is the area
fraction p, which is the mean fraction of area covered by 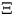 in a region of unit area, i.e.,
in a region of unit area, i.e.,
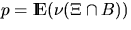 for
for 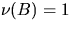 .Because of the stationarity of the Boolean model, this
is also the probability that the origin o
is covered by
.Because of the stationarity of the Boolean model, this
is also the probability that the origin o
is covered by 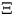 . By application of the Poisson assumption,
p takes the form
. By application of the Poisson assumption,
p takes the form
| 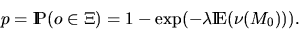 |
(10) |
The Choquet theorem states that the distribution of 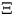 is
uniquely determined by the so-called
capacity functional
is
uniquely determined by the so-called
capacity functional 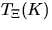 , which is the probability
that
, which is the probability
that 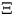 hits a fixed compact set
hits a fixed compact set 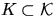 , where
, where
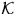 is the family of compact sets in
is the family of compact sets in 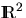 , i.e.,
, i.e.,
| 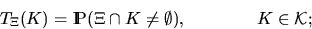 |
(11) |
see Matheron (1975) for a proof of it.
Analogous to Section 2.1 the contact distribution
function H*B(r) is defined for a convex set B containing the origin o
as
| 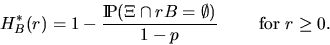 |
(12) |
It holds that
|  |
(13) |
where 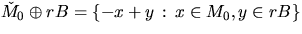 .In the special case where B is the unit disc,
.In the special case where B is the unit disc, 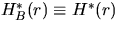 is called the spherical contact distribution function.
is called the spherical contact distribution function.
Further quantities of interest are
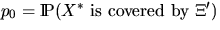 and
and
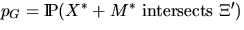 ,where M* is a `typical grain', X* its corresponding germ and
,where M* is a `typical grain', X* its corresponding germ and
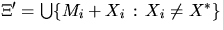 .These probabilities are given by
p0 = p and
.These probabilities are given by
p0 = p and
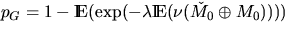 .If the grains are discs of fixed radius r, then
.If the grains are discs of fixed radius r, then
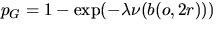 and hence, using
(4.10), pG = 1-(1-p)4.
and hence, using
(4.10), pG = 1-(1-p)4.
The number N of sets in the
Boolean model that intersect a fixed convex subset S0 of  is Poisson-distributed with mean
is Poisson-distributed with mean
| 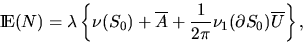 |
(14) |
where 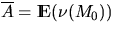 ,
, 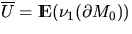 ,
, denotes the one-dimensional Lebesgue measure,
and
denotes the one-dimensional Lebesgue measure,
and  the boundary of the set S0. As a special case,
the number N of sets in the Boolean model that cover the singleton
the boundary of the set S0. As a special case,
the number N of sets in the Boolean model that cover the singleton
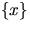 is Poisson-distributed with mean
is Poisson-distributed with mean
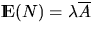 .It follows from (4.14) that the probability q(S0)
that S0 has no intersection with
.It follows from (4.14) that the probability q(S0)
that S0 has no intersection with 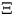 is given by
is given by
| ![\begin{displaymath}
q(S_0) = \exp \{ - \lambda [\oA + \nu (S_0) + \frac{1}{2\pi}
\oU \nu_1(\partial S_0)]\}\end{displaymath}](img160.gif) |
(15) |
in the case that S0 is a fixed convex subset of 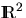 . If
S0 is a singleton, then
. If
S0 is a singleton, then
| 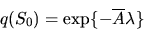 |
(16) |
and if S0 is a line segment of length l, then
| 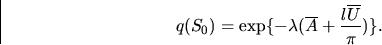 |
(17) |
For the Boolean model where the grains Mn are discs with independent
identically distributed radii Rn with distribution function F,
further Poisson processes can be assigned to (X,M):
consider a fixed (deterministic) line 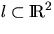 and assume that
and assume that
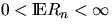 .
Then the sequence Xn* of the projection on l of those
points Xn such that the circle Mn + Xn hits the line l,
forms a (one-dimensional) homogeneous Poisson process on l with intensity
.
Then the sequence Xn* of the projection on l of those
points Xn such that the circle Mn + Xn hits the line l,
forms a (one-dimensional) homogeneous Poisson process on l with intensity
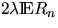 (see Figure 7).
Furthermore, the sequence Xn* together with the sequence of
intersections Mn* of the discs Mn with the line l form a
one-dimensional Boolean model
(see Figure 7).
Furthermore, the sequence Xn* together with the sequence of
intersections Mn* of the discs Mn with the line l form a
one-dimensional Boolean model 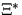 .
.
Figure 7:
Intersection
![\begin{figure}
\beginpicture
\setcoordinatesystem units <0.04mm,0.04mm\gt
\setpl...
...483 513.793 /
\put {\circle*{2}} [Bl] at 784.483 513.793
\endpicture\end{figure}](img167.gif) |
The length of the intersections is
distributed according to G with the density
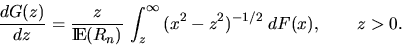
Note that this construction of a linear Boolean model is also valid in a more
general case, namely if the grains are convex sets. In the following we
will restrict ourselves to discs.
The resulting pattern of clumps of intersection segments can be used to
model a variety of phenomena. In mobile communications the two-dimensional
Boolean model 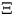 can be interpreted as the users together with their power,
where the germs are the locations of the callers and the grains are
their random power. Hence the clumps of the associated one-dimensional
Boolen model
can be interpreted as the users together with their power,
where the germs are the locations of the callers and the grains are
their random power. Hence the clumps of the associated one-dimensional
Boolen model 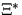 can be interpreted as the regions of interference
on the road and one is interested in the covered and uncovered parts of the
road. The length of such an uncovered part is
exponentially distributed with mean
can be interpreted as the regions of interference
on the road and one is interested in the covered and uncovered parts of the
road. The length of such an uncovered part is
exponentially distributed with mean 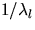 .The length of a typical clump
has a distribution with Laplace-Stieltjes transform
.The length of a typical clump
has a distribution with Laplace-Stieltjes transform
| ![\begin{displaymath}
\gamma(s) = 1 + \frac{s}{\lambda_l} - \left( \lambda_l
\int...
...ambda_l \int\limits_0^t
\, (1-G(x))\,dx\right] dt \right)^{-1};\end{displaymath}](img170.gif) |
(18) |
see e.g. Hall (1988). The distribution can be obtained
numerically using an inversion algorithm for Laplace-Stieltjes transforms,
for example the so-called
Euler-algorithm; see e.g. Rolski et al. (1998).
In Frey (1997) the following approximation is given.
For the distribution of the clump length L it holds that
| 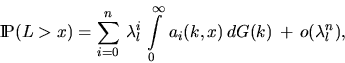 |
(19) |
where the quantities ai(k,x) are recursively given by
| 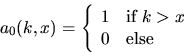 |
(20) |
| 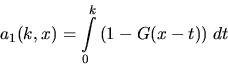 |
(21) |
and for 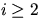
| 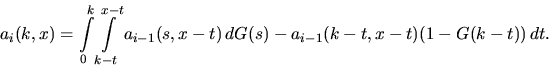 |
(22) |
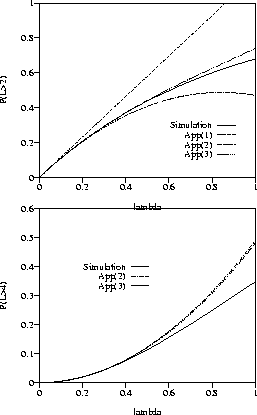
Figure 8 compares the above approximation with simulated values
for x=2 (x=4 respectively) and
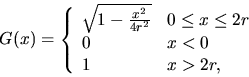
i.e., the radii of the discs in the two-dimensional Boolean model are
fixed and equal to 1. By App(n) we mean the approximation by a polynomial
of degree n given by (4.19).
Figure 8:
Approximations and simulation of the clump length distribution
 |
From (4.19) one can deduce the probability that an interval
of length t is completly covered by the one-dimensional Boolean
model 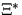 , i.e.,
, i.e.,
where 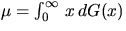 and
the quantities ai(k,x) are given by (4.20) to (4.22).
and
the quantities ai(k,x) are given by (4.20) to (4.22).
Besides the distribution of the length of an uncovered part one
is also interested in the distribution of the sum V of the uncovered
parts in a given interval. Hall (1988) derived a formula
for the distribution of vacancy V in the interval [0,t] provided
that the segment length is fixed. However, this one-dimensional
Boolean model cannot be deduced from a two-dimensional Boolean model.
Frey (1997) showed for general distributed
segment length and hence for a one-dimensional Boolean model which
can be deduced from a two-dimensional Boolean model, that the distribution
of vacancy V in [0,t] is given by
| 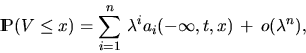 |
(23) |
provided that 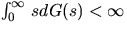 , where the
quantities ai(k,t,x) are recursively given by
, where the
quantities ai(k,t,x) are recursively given by
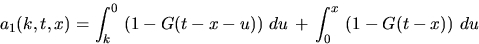
and for 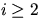
Similar problems where the grains are sticks were considered in
B aszczyszyn et al. (1997), Rau (1997).
They derived
a Taylor-series expansion w.r.t. the intensity
aszczyszyn et al. (1997), Rau (1997).
They derived
a Taylor-series expansion w.r.t. the intensity 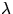 for the expectation of the typical clump length and calculated
the first coefficients numerically.
for the expectation of the typical clump length and calculated
the first coefficients numerically.



Next: Statistical Analysis of Boolean
Up: The Boolean Model
Previous: The Boolean Model
Andreas Frey
7/8/1998
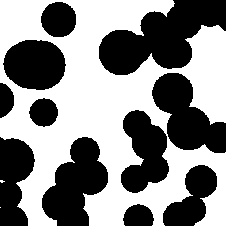
![]() in a region of unit area, i.e.,
in a region of unit area, i.e.,
![]() for
for ![]() .Because of the stationarity of the Boolean model, this
is also the probability that the origin o
is covered by
.Because of the stationarity of the Boolean model, this
is also the probability that the origin o
is covered by ![]() . By application of the Poisson assumption,
p takes the form
. By application of the Poisson assumption,
p takes the form
![]() and
and
![]() ,where M* is a `typical grain', X* its corresponding germ and
,where M* is a `typical grain', X* its corresponding germ and
![]() .These probabilities are given by
p0 = p and
.These probabilities are given by
p0 = p and
![]() .If the grains are discs of fixed radius r, then
.If the grains are discs of fixed radius r, then
![]() and hence, using
(4.10), pG = 1-(1-p)4.
and hence, using
(4.10), pG = 1-(1-p)4.
![]() is Poisson-distributed with mean
is Poisson-distributed with mean
![]() and assume that
and assume that
![]() .
Then the sequence Xn* of the projection on l of those
points Xn such that the circle Mn + Xn hits the line l,
forms a (one-dimensional) homogeneous Poisson process on l with intensity
.
Then the sequence Xn* of the projection on l of those
points Xn such that the circle Mn + Xn hits the line l,
forms a (one-dimensional) homogeneous Poisson process on l with intensity
![]() (see Figure 7).
Furthermore, the sequence Xn* together with the sequence of
intersections Mn* of the discs Mn with the line l form a
one-dimensional Boolean model
(see Figure 7).
Furthermore, the sequence Xn* together with the sequence of
intersections Mn* of the discs Mn with the line l form a
one-dimensional Boolean model ![]() .
.
![]()
![]() can be interpreted as the users together with their power,
where the germs are the locations of the callers and the grains are
their random power. Hence the clumps of the associated one-dimensional
Boolen model
can be interpreted as the users together with their power,
where the germs are the locations of the callers and the grains are
their random power. Hence the clumps of the associated one-dimensional
Boolen model ![]() can be interpreted as the regions of interference
on the road and one is interested in the covered and uncovered parts of the
road. The length of such an uncovered part is
exponentially distributed with mean
can be interpreted as the regions of interference
on the road and one is interested in the covered and uncovered parts of the
road. The length of such an uncovered part is
exponentially distributed with mean ![]() .The length of a typical clump
has a distribution with Laplace-Stieltjes transform
.The length of a typical clump
has a distribution with Laplace-Stieltjes transform
![\begin{displaymath}
\gamma(s) = 1 + \frac{s}{\lambda_l} - \left( \lambda_l
\int...
...ambda_l \int\limits_0^t
\, (1-G(x))\,dx\right] dt \right)^{-1};\end{displaymath}](img170.gif)
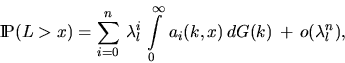
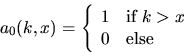
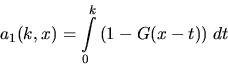
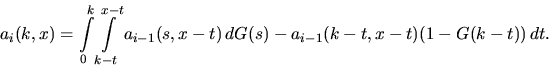
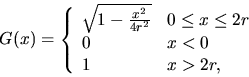
![]() , i.e.,
, i.e.,
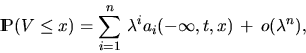
![]()