


Next: A Spatial Ergodic Theorem
Up: Stationary Marked Point Processes
Previous: Stationary Marked Point Processes
Suppose that (X,M) is stationary, with intensity ![$\lambda
= \Exp X_M ([0,1]^2 \times J)$](img111.gif) such that
such that 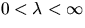 .
Define for
.
Define for 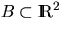 ,
, 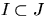
| 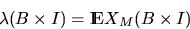 |
(1) |
which is called the intensity measure of (X,M).
By the stationarity of (X,M) we have
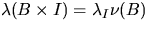 ,where
,where ![$\lambda_I = \lambda ([0,1]^2 \times I)$](img116.gif) is the so-called
I-intensity of (X,M), i.e.,
is the so-called
I-intensity of (X,M), i.e., 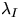 is the expected
number of points per unit area with marks in I.
Now, the so-called Palm mark distribution PM is defined
by the ratio
is the expected
number of points per unit area with marks in I.
Now, the so-called Palm mark distribution PM is defined
by the ratio
| 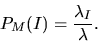 |
(2) |
Andreas Frey
7/8/1998