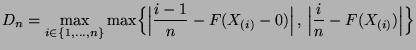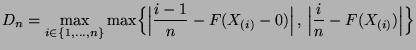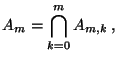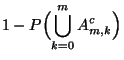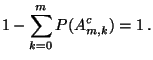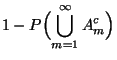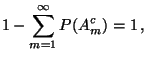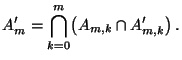Next: Verteilung des maximalen Schätzfehlers
Up: Empirische Verteilungsfunktion
Previous: Definition und elementare Eigenschaften
Contents
Satz von Gliwenko-Cantelli
- Beachte
-
- Beweis
-
- Wir nehmen zunächst an, daß die Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img394.png) stetig ist.
stetig ist.
- Für jede natürliche Zahl
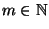 gibt es dann reelle Zahlen
gibt es dann reelle Zahlen
 , so daß
und
, so daß
und
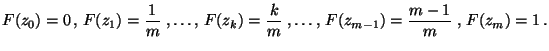 |
(71) |
- Mit der Schreibweise
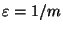 ergibt sich dann hieraus,
daß für jedes
ergibt sich dann hieraus,
daß für jedes
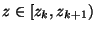
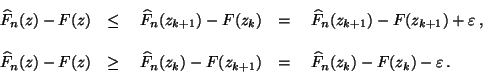 |
(72) |
- Für beliebige
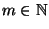 und
und
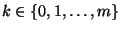 sei
sei
- Aus Teilaussage 3 von Theorem 1.17 ergibt sich dann,
daß
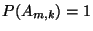 |
(73) |
für beliebige
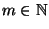 und
und
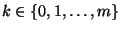 .
.
- Damit gilt auch
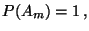 |
(74) |
wobei
denn aus (73) ergibt sich, daß
- Für jedes
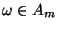 gibt es nun eine natürliche Zahl
gibt es nun eine natürliche Zahl
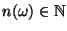 , so daß
für jedes
, so daß
für jedes
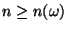 und für jedes
und für jedes
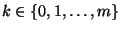 .
.
- Hieraus und aus (72) folgt, daß
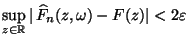 |
(75) |
für jedes
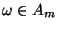 und für jedes
und für jedes
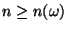 .
.
- Dies bedeutet, daß es für jedes
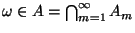 und für jedes
und für jedes
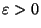 eine natürliche Zahl
eine natürliche Zahl
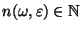 gibt, so daß (75) für
jedes
gibt, so daß (75) für
jedes
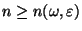 gilt.
gilt.
- Dabei ergibt sich genauso wie im Beweis von (74),
daß
weil
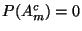 für jedes
für jedes
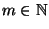 .
.
- Weil
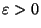 beliebig klein gewählt werden kann, ist somit
die Behauptung (70) für den Fall bewiesen, daß die
Verteilungsfunktion
beliebig klein gewählt werden kann, ist somit
die Behauptung (70) für den Fall bewiesen, daß die
Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img394.png) stetig ist.
stetig ist.
- Im Fall einer beliebigen (nichtnotwendig stetigen)
Verteilungsfunktion
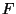 läßt sich die Gültigkeit von
(70) auf ähnliche Weise zeigen.
läßt sich die Gültigkeit von
(70) auf ähnliche Weise zeigen.
- Anstelle von (71) nutzen wir nun die Tatsache, daß
es für jede natürliche Zahl
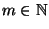 reelle Zahlen
reelle Zahlen
 gibt, so daß
und für jedes
gibt, so daß
und für jedes
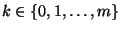
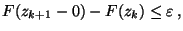 |
(76) |
wobei
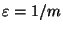 .
.
- Außerdem ergibt sich genauso wie bei der Herleitung von
(72), daß für jedes
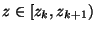
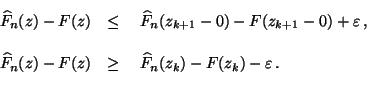 |
(77) |
- Aus Teilaussage 3 von Theorem 1.17 ergibt sich
ähnlich wie (73), daß
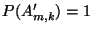 für
beliebige
für
beliebige
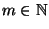 und
und
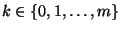 , wobei
, wobei
- Hieraus und aus (77) folgt dann, daß
(75) für jedes
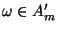 und für jedes
und für jedes
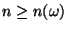 gilt, wobei
gilt, wobei
- Weil
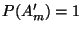 für jedes
für jedes
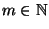 , ergibt sich nun die
Behauptung genauso wie im ersten Teil des Beweises.
, ergibt sich nun die
Behauptung genauso wie im ersten Teil des Beweises.

- Beachte
 Ein JAVA-Applet, mit dem die Aussage des Satzes von
Gliwenko-Cantelli, d.h. der Grenzübergang
(70) simuliert werden kann, findet man
beispielsweise auf der Internet-Seite:
Dieses JAVA-Applet simuliert die empirische
Tailfunktion
Ein JAVA-Applet, mit dem die Aussage des Satzes von
Gliwenko-Cantelli, d.h. der Grenzübergang
(70) simuliert werden kann, findet man
beispielsweise auf der Internet-Seite:
Dieses JAVA-Applet simuliert die empirische
Tailfunktion
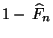 für den Fall, daß
für den Fall, daß
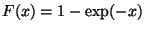 für
für 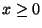 , d.h.,
, d.h., 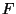 ist die Verteilungsfunktion der
Exponentialverteilung Exp
ist die Verteilungsfunktion der
Exponentialverteilung Exp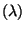 mit dem Parameter
mit dem Parameter 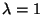 .
.




Next: Verteilung des maximalen Schätzfehlers
Up: Empirische Verteilungsfunktion
Previous: Definition und elementare Eigenschaften
Contents
Roland Maier
2003-03-06