- Ein einfacher Computer-Algorithmus zur Monte-Carlo-Simulation der
Zahl
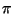 ist die folgende (verbesserte) Variante des
Buffonschen Nadelexperimentes, vgl. auch die Abschnitte 2.5 bzw.
5.2.3 der Vorlesung ,,Wahrscheinlichkeitsrechnung''.
ist die folgende (verbesserte) Variante des
Buffonschen Nadelexperimentes, vgl. auch die Abschnitte 2.5 bzw.
5.2.3 der Vorlesung ,,Wahrscheinlichkeitsrechnung''.
- Dieser Algorithmus hängt mit dem folgenden geometrischen
Sachverhalt zusammen.
- Wir betrachten das Quadrat
![$\displaystyle B=(-1,1]\times(-1,1]\subset\mathbb{R}^2
$](img1027.png)
- bzw. den in
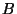 einbeschriebenen Kreis
einbeschriebenen Kreis
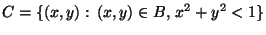
- und werfen einen Punkt willkürlich in die Menge
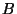 .
.
- Wir betrachten das Quadrat
- In der Sprechweise der Stochastik bedeutet dies:
- Wir betrachten zwei unabhängige
Zufallsvariablen
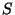 und
und 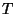 , die jeweils
gleichverteilt im Intervall
, die jeweils
gleichverteilt im Intervall ![$ (-1,1]$](img897.png) sind,
und
sind,
und
- bestimmen die Wahrscheinlichkeit des Ereignisses
dass der ,,zufällige Punkt''
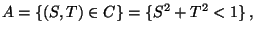
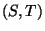 in
in
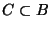 liegt.
liegt.
- Dann gilt
wobei
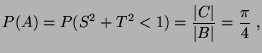
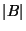 ,
, 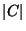 den Flächeninhalt von
den Flächeninhalt von 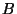 bzw.
bzw.
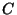 bezeichnet.
bezeichnet.
- Wir betrachten zwei unabhängige
Zufallsvariablen
- Ähnlich wie beim Buffonschen Nadelexperiment
ergibt sich nun aus der Gleichung
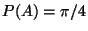 eine
eine
- Methode zur statistischen Schätzung der Zahl
 ,
,
- die auf dem Gesetz der großen Zahlen beruht und die sich leicht implementieren lässt.
- Methode zur statistischen Schätzung der Zahl
- Und zwar seien
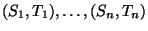 unabhängige und
identisch verteilte Zufallsvektoren,
unabhängige und
identisch verteilte Zufallsvektoren,
- deren Verteilung mit der
Verteilung von
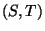 übereinstimmt und
übereinstimmt und
- die wir als ein stochastisches Modell für
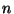 (unabhängig durchgeführte) Experimente auffassen.
(unabhängig durchgeführte) Experimente auffassen.
- Dann sind
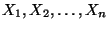 mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert
mit
unabhängige und identisch verteilte Zufallsvariablen mit dem Erwartungswert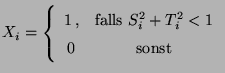
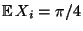 .
.
- deren Verteilung mit der
Verteilung von
- Aus dem starken Gesetz der großen Zahlen (vgl. Theorem WR-5.15)
ergibt sich darüber hinaus, dass
- das arithmetische Mittel
fast sicher gegen die Zahl
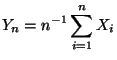
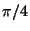 strebt.
strebt.
- Somit ist
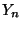 ein erwartungstreuer und (stark)
konsistenter Schätzer für
ein erwartungstreuer und (stark)
konsistenter Schätzer für
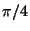 ,
,
- d.h., für große
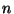 ist
ist 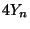 mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
mit
hoher Wahrscheinlichkeit eine gute Näherung der Zahl
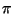 .
.
- das arithmetische Mittel
- Bei der Implementierung dieser Simulationsalgorithmus
kann man wie folgt vorgehen.
- Erzeuge
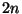 in
in ![$ (0,1]$](img167.png) gleichverteilte Pseudozufallszahlen
gleichverteilte Pseudozufallszahlen
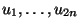 mit einem
Zufallszahlengenerator.
mit einem
Zufallszahlengenerator.
- Setze
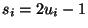 und
und
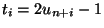 für
für
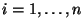 .
.
- Setze
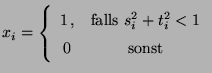
- Berechne
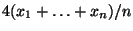 .
.
- Erzeuge
- Sei
![$ \varphi:[0,1]\to[0,1]$](img1053.png) eine stetige Funktion.
eine stetige Funktion.
- Gesucht ist ein Schätzer für den Wert des Integrals
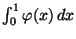 , der mit Monte-Carlo-Simulation bestimmt
werden soll.
, der mit Monte-Carlo-Simulation bestimmt
werden soll.
- Dabei betrachten wir das folgende stochastische Modell.
- Gesucht ist ein Schätzer für den Wert des Integrals
- Seien
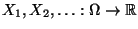 unabhängige und identisch
verteilte Zufallsvariable, die im Intervall
unabhängige und identisch
verteilte Zufallsvariable, die im Intervall ![$ (0,1]$](img167.png) gleichverteilt
sind.
gleichverteilt
sind.
- Außerdem sei
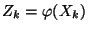 für jedes
für jedes
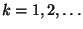 .
.
- Wegen des Transformationssatzes für unabhängige Zufallsvariablen
(vgl. Theorem WR-3.18) sind dann auch
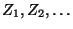 unabhängige
und identisch verteilte Zufallsvariable,
unabhängige
und identisch verteilte Zufallsvariable,
- und es gilt
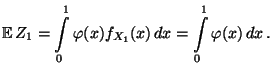
- Außerdem sei
- Aus dem starken Gesetz der großen Zahlen (vgl. Theorem WR-5.15)
ergibt sich darüber hinaus, dass für
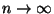
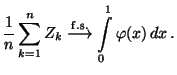
- Somit ist
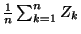 ein erwartungstreuer
und (stark) konsistenter Schätzer für
ein erwartungstreuer
und (stark) konsistenter Schätzer für
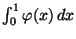 ,
,
- d.h., für große
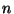 ist
ist
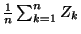 mit
hoher Wahrscheinlichkeit eine gute Näherung des
Integrals
mit
hoher Wahrscheinlichkeit eine gute Näherung des
Integrals
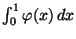 .
.
- Somit ist
- Bei der Implementierung dieses Simulationsalgorithmus kann man ähnlich wie in Beispiel 1
vorgehen:
- Erzeuge
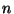 in
in ![$ (0,1]$](img167.png) gleichverteilte Pseudozufallszahlen
gleichverteilte Pseudozufallszahlen
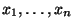 mit einem
Zufallszahlengenerator.
mit einem
Zufallszahlengenerator.
- Setze
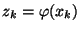 für
für
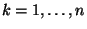 .
.
- Berechne
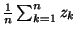 .
.
- Erzeuge