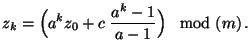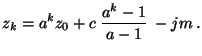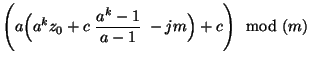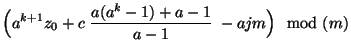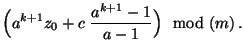Nächste Seite: Tests von Güteeigenschaften
Aufwärts: Erzeugung von Pseudozufallszahlen
Vorherige Seite: Einfache Anwendungsbeispiele; Monte-Carlo-Schätzer
Inhalt
Lineare Kongruenzgeneratoren
- Den Ausgangspunkt der meisten Simulationsalgorithmen bilden Standard-Zufallszahlen-Generatoren,
- deren Ziel darin besteht, Folgen
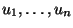 von Zahlen aus
dem Einheitsintervall
von Zahlen aus
dem Einheitsintervall ![$ (0,1]$](img167.png) zu erzeugen, sogenannte Standard-Pseudozufallszahlen,
zu erzeugen, sogenannte Standard-Pseudozufallszahlen,
- die als Realisierungen von unabhängigen und (identisch in
![$ (0,1]$](img167.png) )
gleichverteilten Zufallsvariablen
)
gleichverteilten Zufallsvariablen
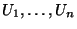 aufgefasst
werden können.
aufgefasst
werden können.
- Ein weit verbreitetes Verfahren zur Erzeugung von
Standard-Pseudozufallszahlen ist die folgende lineare
Kongruenzmethode,
Wir lösen nun die Rekursionsgleichung (1), d.h.,
wir zeigen, wie sich die in (1) rekursiv
definierte Zahl 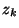 direkt durch den Startwert
direkt durch den Startwert 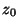 sowie
durch die Parameter
sowie
durch die Parameter 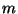 ,
, 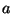 bzw.
bzw. 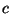 ausdrücken lässt.
ausdrücken lässt.
- Beweis
-
- Beachte
-
Wir erwähnen nun (hinreichende und notwendige) Bedingungen an die
Parameter 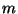 ,
, 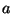 ,
, 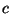 bzw.
bzw. 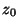 , die insbesondere sichern, dass
die maximal mögliche Periode
, die insbesondere sichern, dass
die maximal mögliche Periode 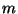 erreicht wird.
erreicht wird.
Theorem 3.2
- 1.
- Falls
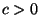 , so erzeugt der in
, so erzeugt der in
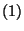 definierte
lineare Kongruenzgenerator genau dann für jeden Startwert
definierte
lineare Kongruenzgenerator genau dann für jeden Startwert
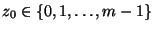 eine Zahlenfolge
eine Zahlenfolge
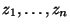 mit
der maximal möglichen Periode
mit
der maximal möglichen Periode 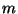 , wenn die folgenden Bedingungen
erfüllt sind:
, wenn die folgenden Bedingungen
erfüllt sind:
- (a
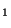 )
)
- Die Parameter
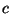 und
und 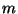 sind teilerfremd.
sind teilerfremd.
- (a
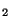 )
)
- Für jede Primzahl
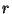 , die
, die 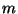 teilt, ist
teilt, ist 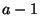 ein Vielfaches von
ein Vielfaches von 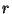 .
.
- (a
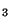 )
)
- Falls
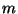 ein Vielfaches von
ein Vielfaches von 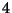 ist, dann ist
auch
ist, dann ist
auch 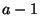 ein Vielfaches von
ein Vielfaches von 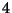 .
.
- 2.
- Falls
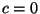 , so gilt
, so gilt 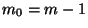 für jedes
für jedes
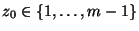 genau dann, wenn
genau dann, wenn
- (b
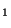 )
)
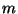 eine Primzahl ist,
eine Primzahl ist,
- (b
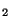 )
)
- für jede Primzahl
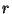 , die
, die 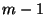 teilt, die
Zahl
teilt, die
Zahl
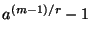 nicht durch
nicht durch 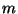 teilbar ist.
teilbar ist.
- 3.
- Falls
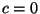 und falls es ein
und falls es ein
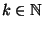 mit
mit
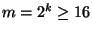 gibt, so
gilt
gibt, so
gilt 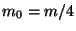 genau dann, wenn
genau dann, wenn 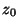 eine ungerade Zahl ist und
wenn
eine ungerade Zahl ist und
wenn
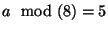 oder
oder 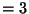 gilt.
gilt.
- Einen Beweis von Theorem 3.2, in dem
Ergebnisse der Zahlentheorie (u.a. der kleine Satz von Fermat)
verwendet werden, kann man beispielsweise
- in Abschnitt 2.7 des Buches von B.D. Ripley (1987) Stochastic
Simulation, J. Wiley & Sons, New York oder
- in Abschnitt 3.2 von D.E. Knuth (1997) The Art of Computer
Programming, Vol. II, Addison-Wesley, Reading MA finden.
- Darüber hinaus verweisen wir auch auf diese beiden Bücher
hinsichtlich der Diskussion
- von anderen Generatoren zur Erzeugung von
Standard-Pseudozufallszahlen wie beispielsweise nichtlineare
Kongruenzgeneratoren, Schieberegister-Generatoren,
Lagged-Fibonacci-Generatoren sowie die Kombination solcher
Generatoren,
- von alternativen Bedingungen an die Parameter
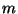 ,
, 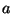 ,
, 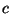 bzw.
bzw.
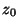 des linearen Kongruenzgenerators, der in (1)
definiert wurde,
des linearen Kongruenzgenerators, der in (1)
definiert wurde,
- um Zahlenfolgen
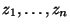 mit einer möglichst großen
Periode
mit einer möglichst großen
Periode 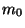 und mit weiteren Güteeigenschaften zu erzeugen.
und mit weiteren Güteeigenschaften zu erzeugen.
- Eine solche Güteeigenschaft besteht darin,
- dass die Punkte
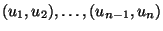 von jeweils
aufeinanderfolgenden Pseudozufallszahlen
von jeweils
aufeinanderfolgenden Pseudozufallszahlen 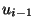 ,
, 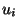 das
Einheitsquadrat
das
Einheitsquadrat ![$ [0,1]^2$](img1115.png) möglichst gleichmäßig ausfüllen,
möglichst gleichmäßig ausfüllen,
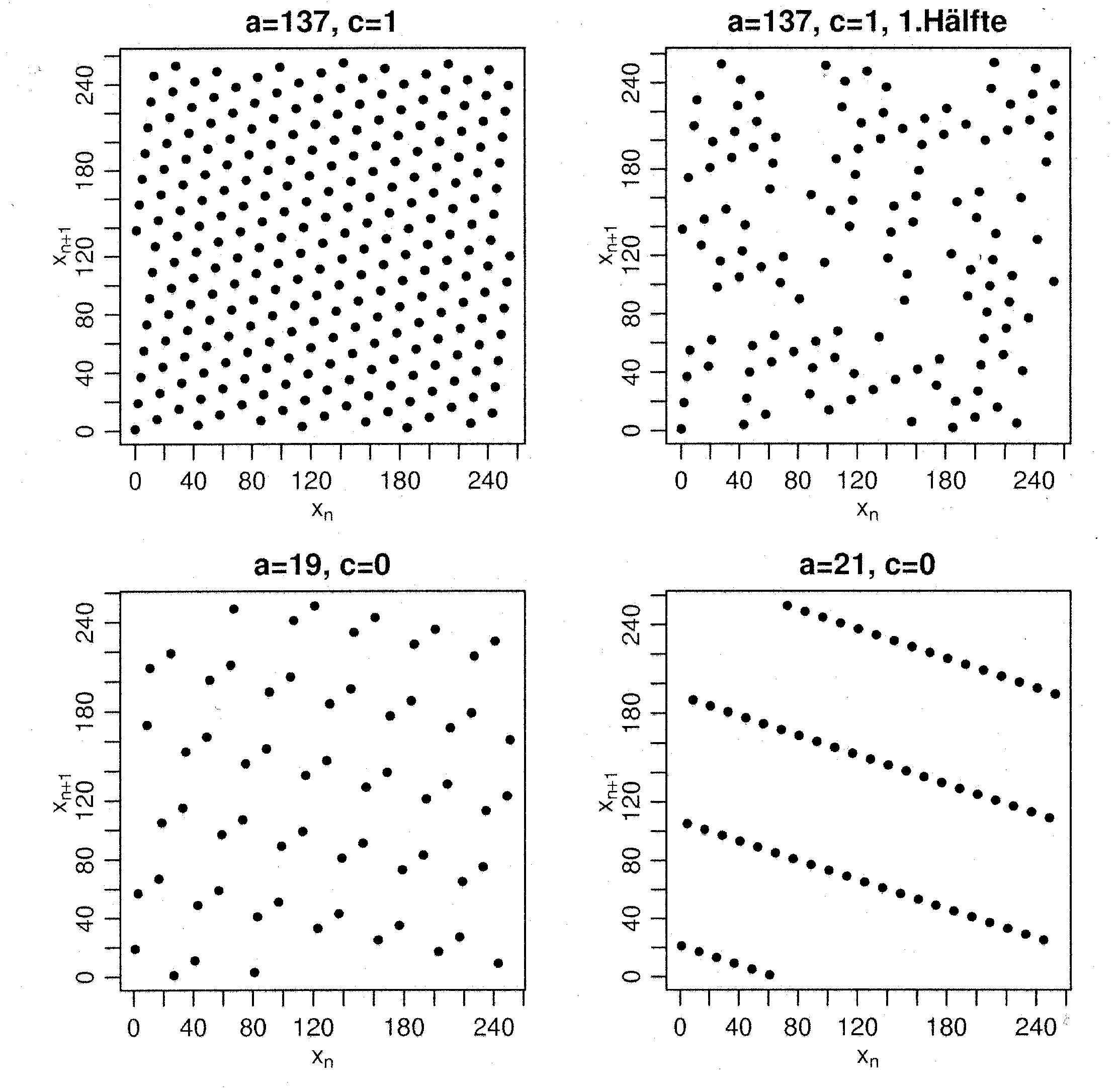
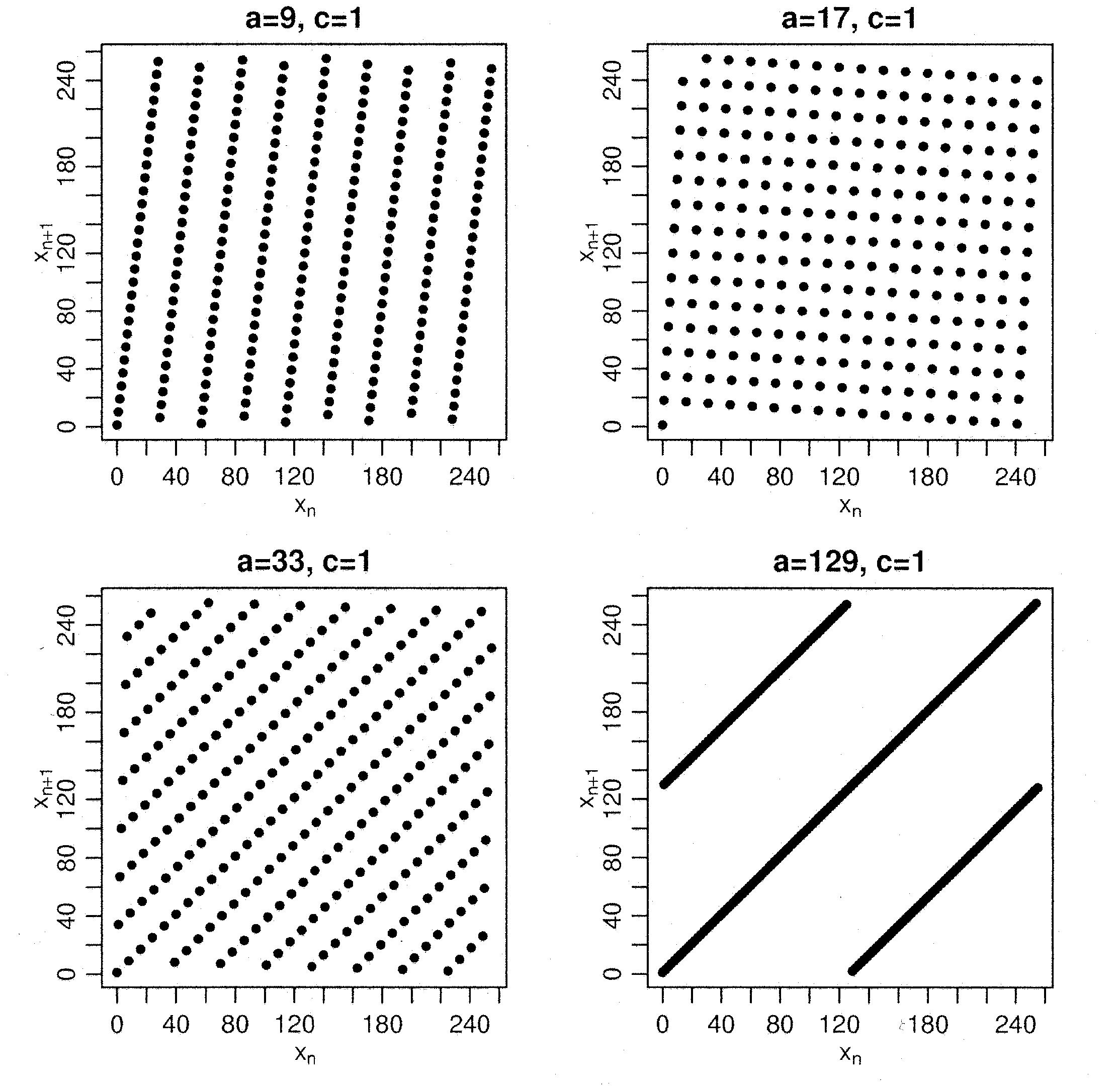
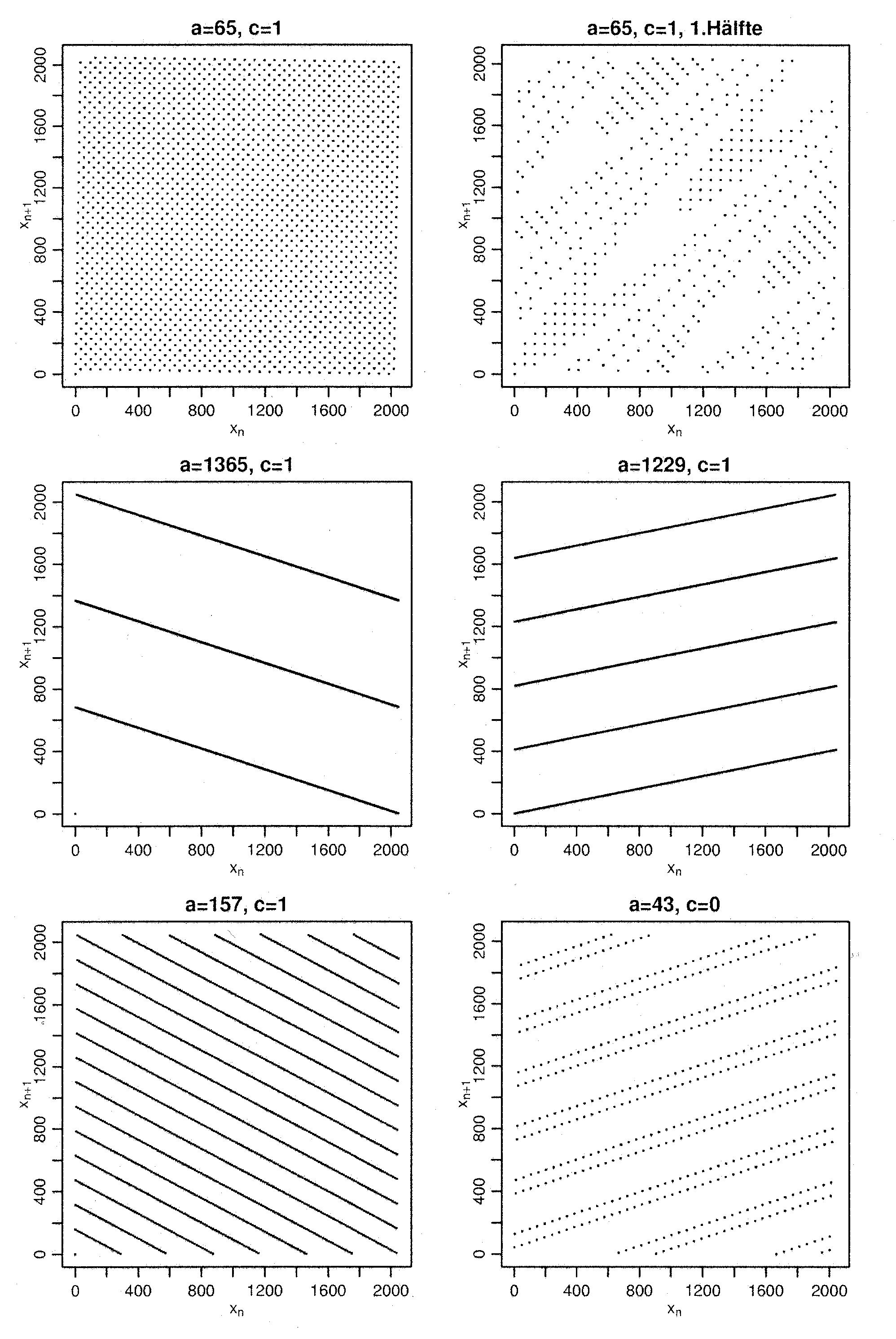
- wobei die folgenden Zahlenbeispiele verdeutlichen, dass relativ
geringfügige Änderungen der Parameter
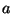 und
und 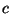 zu völlig
unterschiedlichen Punktmustern
zu völlig
unterschiedlichen Punktmustern
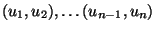 führen können.
führen können.
- Weitere Details hierzu sind beispielsweise in dem bereits
erwähnten Buch von Ripley (1987) bzw. in dem Vorlesungsskipt von
H. Künsch unter ftp://stat.ethz.ch/U/Kuensch/skript-sim.ps zu
finden, wo auch die folgenden Abbildungen enthalten sind.
Abbildung:
Punktmuster für Paare
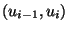 aufeinanderfolgender Pseudozufallszahlen mit
aufeinanderfolgender Pseudozufallszahlen mit 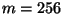
|
|
Abbildung:
Punktmuster für Paare
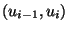 aufeinanderfolgender Pseudozufallszahlen mit
aufeinanderfolgender Pseudozufallszahlen mit 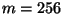
|
|
Abbildung:
Punktmuster für Paare
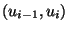 aufeinanderfolgender Pseudozufallszahlen mit
aufeinanderfolgender Pseudozufallszahlen mit 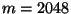
|
|




Nächste Seite: Tests von Güteeigenschaften
Aufwärts: Erzeugung von Pseudozufallszahlen
Vorherige Seite: Einfache Anwendungsbeispiele; Monte-Carlo-Schätzer
Inhalt
Ursa Pantle
2003-09-29
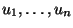 von Zahlen aus
dem Einheitsintervall
von Zahlen aus
dem Einheitsintervall ![$ (0,1]$](img167.png) zu erzeugen, sogenannte Standard-Pseudozufallszahlen,
zu erzeugen, sogenannte Standard-Pseudozufallszahlen,
![$ (0,1]$](img167.png) )
gleichverteilten Zufallsvariablen
)
gleichverteilten Zufallsvariablen
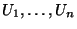 aufgefasst
werden können.
aufgefasst
werden können.
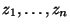 gemäß einer Rekursion
vom Typ
gemäß einer Rekursion
vom Typ
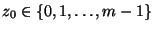 ausgegangen, der auch Keim des linearen Kongruenzgenerators
genannt wird, und
ausgegangen, der auch Keim des linearen Kongruenzgenerators
genannt wird, und
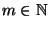 ,
,
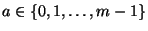 bzw.
bzw.
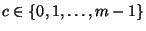 sind weitere Parameter, die Modul, Faktor bzw. Inkrement des Kongruenzgenerators genannt werden.
sind weitere Parameter, die Modul, Faktor bzw. Inkrement des Kongruenzgenerators genannt werden.
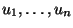 .
.