- Und zwar zerlegen wir die Zufallsstichprobe
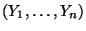 in
in
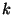 Teilstichproben
Teilstichproben
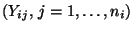 , wobei angenommen
wird, dass
, wobei angenommen
wird, dass 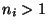 für jedes
für jedes
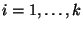 und
und
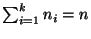 .
.
- Außerdem setzen wir voraus, dass die Stichprobenvariablen, die zu einundderselben Teilstichprobe gehören, jeweils den gleichen Erwartungswert haben.
gilt, wobei
-
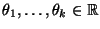 (unbekannte) Modellparameter
sind,
(unbekannte) Modellparameter
sind,
- die Störgrößen
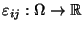 unabhängig sind mit
unabhängig sind mit
- und die Varianzen
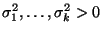 ebenfalls
unbekannte Modellparameter sind.
ebenfalls
unbekannte Modellparameter sind.
- Die Nummern
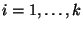 der Teilstichproben
der Teilstichproben
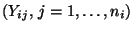 werden als Stufen eines Einflussfaktors
gedeutet.
werden als Stufen eines Einflussfaktors
gedeutet.
- Von besonderem Interesse ist der Fall, dass
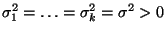 . In diesem Fall spricht
man von homoskedastischen Störgrößen, ansonsten von heteroskedastischen Störgrößen.
. In diesem Fall spricht
man von homoskedastischen Störgrößen, ansonsten von heteroskedastischen Störgrößen.
- Die obengemachten Modellannahmen bedeuten insbesondere, dass die
beobachteten Werte
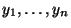 der Zielvariablen
der Zielvariablen
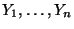 wie folgt tabellarisch strukturiert werden
können:
wie folgt tabellarisch strukturiert werden
können:
Stufe 1 2 3 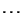
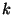
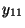
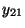
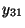
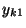
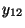
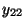
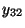
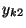
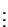
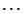
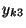
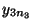
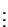
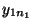
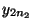
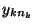
- Der Begriff ,,Varianzanalyse'' bedeutet nicht, dass die
Varianzen der Stichprobenvariablen
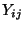 untersucht werden,
sondern es handelt sich um die Analyse der Variabilität der
Erwartungswerte
untersucht werden,
sondern es handelt sich um die Analyse der Variabilität der
Erwartungswerte
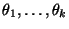 .
.
- In der englischsprachigen Literatur ist die Abkürzung ANOVA üblich (ANOVA = analysis of variance).
- Eine Gruppe von 12 Personen führte das folgende Copmuter-Experiment durch.
- Dabei standen 3 verschiedene Tastaturen zur Verfügung, um einen vorgegebenen Text jeweils eine Minute lang in einen PC einzugeben.
- Es nutzen 5 Personen die erste Tastatur, 3 Personen die zweite
Tastatur und 4 Personen die dritte Tastatur, wobei jeweils die
folgenden Anzahlen von Wörtern je Minute in den PC eingegeben
wurden:
Tastatur 1 2 3 79 74 81 83 85 65 62 72 79 51 55 77
- Der Einflussfaktor ,,Tastatur'' hat also in diesem Fall
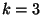 ,,Stufen'' mit
,,Stufen'' mit 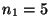 ,
, 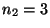 bzw.
bzw. 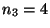 .
.
- Die Größen
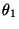 ,
, 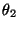 bzw.
bzw. 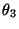 sind dabei
jeweils die erwarteten Anzahlen von Wörtern, die mit der ersten,
zweiten bzw. dritten Tastatur je Minute in den PC eingegeben
werden.
sind dabei
jeweils die erwarteten Anzahlen von Wörtern, die mit der ersten,
zweiten bzw. dritten Tastatur je Minute in den PC eingegeben
werden.