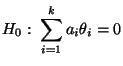- ob die Erwartungswerte
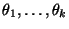 der
Stichprobenvariablen
der
Stichprobenvariablen 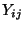 gleich sind, also nicht von der
Nummer
gleich sind, also nicht von der
Nummer 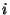 der betrachteten Teilstichprobe abhängen,
der betrachteten Teilstichprobe abhängen,
- d.h., wir prüfen die Hypothese, ob die Stufen des Einflussfaktors keine statistische Signifikanz haben.
- Beim Testen der ANOVA-Nullhypothese
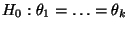 ist es nützlich zu beachten, dass diese Hypothese mit Hilfe von
sogenannten Kontraste ausgedrückt werden kann.
ist es nützlich zu beachten, dass diese Hypothese mit Hilfe von
sogenannten Kontraste ausgedrückt werden kann.
- Unter einem Kontrast versteht man dabei die folgenden
Abbildung:
wobei
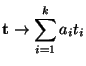
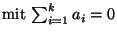
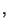
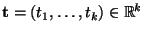 ein beliebiger Vektor von
Variablen und
ein beliebiger Vektor von
Variablen und
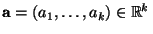 ein Vektor von
(bekannten) Konstanten ist.
ein Vektor von
(bekannten) Konstanten ist.
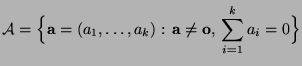
d.h., jeder Kontrast nimmt im Punkt
- die Hypothese
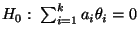 für einen
vorgegebenen Kontrast
für einen
vorgegebenen Kontrast
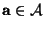 betrachtet,
betrachtet,
- d.h., es wird zunächst ein hypothetischer Wert für die Linearkombination
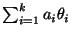 der
Erwartungswerte
der
Erwartungswerte
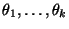 getestet.
getestet.