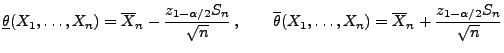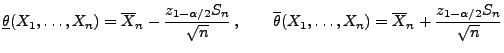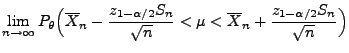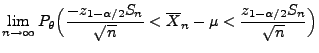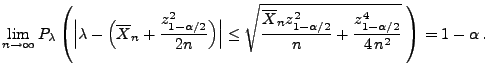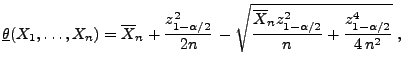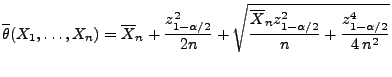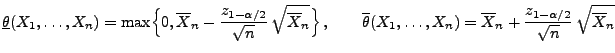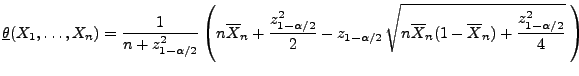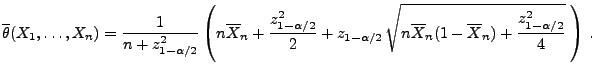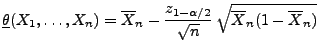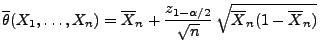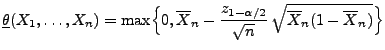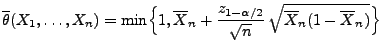Ein-Stichproben-Probleme

Wir kehren zunächst zur Betrachtung von Ein-Stichproben-Problemen zurück. D.h., wir nehmen an, dass ein Datensatz $(x_1,\ldots,x_n)$ beobachtet wird, den wir als Realisierung einer Zufallsstichprobe $(X_1,\ldots,X_n)$ auffassen.

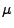
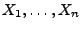
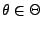
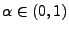
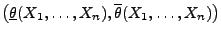
Theorem 3.2   Der Erwartungswert $\mu$ der Stichprobenvariablen $X_1,\ldots,X_n$ sei eine Komponente des Parameters $\theta\in\Theta$, und $\alpha\in(0,1)$ sei eine beliebige, jedoch vorgegebene Zahl. Dann ist durch $\bigl(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n)\bigr)$ mit

$$\underline\theta(X_1,\ldots,X_n)=\overline X_n-\frac{z_{1-\alpha... ...rline\theta(X_1,\ldots,X_n)=\overline X_n+\frac{z_{1-\alpha/2}S_n}{\sqrt{n}}$$

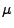
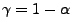
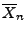
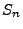
ein asymptotisches Konfidenzintervall für $\mu$ zum Niveau $\gamma=1-\alpha$ gegeben, wobei $\overline X_n$ bzw. $S_n$ das Stichprobenmittel bzw. die Wurzel der Stichprobenvarianz sind.

Beweis

$\;$ Die Behauptung ergibt sich unmittelbar aus Formel (1.20), denn

$$\lim\limits_{n\to\infty} P_\theta\Bigl(\overline X_n-\frac{z_{1-\alpha/2}S_n}{\sqrt{n}}<\mu<\overline X_n+\frac{z_{1-\alpha/2}S_n}{\sqrt{n}}\Bigr) = \lim\limits_{n\to\infty} P_\theta\Bigl(\frac{-z_{1-\alpha/2}S_n}{\sqrt{n}}<\overline X_n-\mu<\frac{z_{1-\alpha/2}S_n}{\sqrt{n}}\Bigr)$$

$$= 1-\alpha\,.$$

 
  $\Box$

Für spezielle Beispiele von Familien parametrischer Verteilungen kann man asymptotische Konfidenzintervalle für den Erwartungswert $\mu$ der Stichprobenvariablen $(X_1,\ldots,X_n)$ konstruieren, ohne die Stichprobenstreuung $S_n^2$ betrachten zu müssen.

1. $\;$ Konfidenzintervall für den Erwartungswert $\lambda$ bei Poisson-Verteilung
   • Wir nehmen an, dass $X_i\sim$ Poi$(\lambda)$ für ein (unbekanntes) $\lambda>0$.
   • Weil dann ${\mathbb{E}\,}X_i=\lambda$ und ${\rm Var\,}X_i=\lambda$ gilt, ergibt sich aus dem zentralen Grenzwertsatz für Summen von unabhängigen und identisch verteilten Zufallsvariablen (vgl. Theorem WR-5.16), dass für jedes $\alpha\in(0,1)$

     $$\lim\limits _{n\to\infty} P_\lambda\Bigl(-z_{1-\alpha/2}\le\sqrt... ...rac{\overline X_n-\lambda}{\sqrt{\lambda}}\le z_{1-\alpha/2}\Bigr)=1-\alpha\,.$$ (30)

     
     

   • Durch Quadrierung der Ungleichungen in (30) und anschließende Auflösung nach $\lambda$ ergibt sich, dass (30) äquivalent ist mit
     $$\lim\limits _{n\to\infty} P_\lambda\left(\Bigl\vert\lambda-\Bigl... ... z^2_{1-\alpha/2}}{n}+\frac{z^4_{1-\alpha/2}}{4\,n^2}}\; \right)=1-\alpha\,.$$

   • Also ist mit
     $$\underline\theta(X_1,\ldots,X_n)=\overline X_n+\frac{z^2_{1-\alp... ...\frac{\overline X_n z^2_{1-\alpha/2}}{n}+\frac{z^4_{1-\alpha/2}}{4\,n^2}}\;,$$
     $$\overline\theta(X_1,\ldots,X_n)=\overline X_n+\frac{z^2_{1-\alph... ...rt{\frac{\overline X_n z^2_{1-\alpha/2}}{n}+\frac{z^4_{1-\alpha/2}}{4\,n^2}}$$
     ein asymptotisches Konfidenzintervall $(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n))$ für $\lambda$ zum Niveau $\gamma=1-\alpha$ gegeben.
   • Für die Länge dieses Konfidenzintervalls gilt

     $$\overline\theta(X_1,\ldots,X_n)-\underline\theta(X_1,\ldots,X_n) ... ...t{\frac{\overline X_n z^2_{1-\alpha/2}}{n}+\frac{z^4_{1-\alpha/2}}{4\,n^2}}\;.$$ (31)

     
     

   Beachte

    $&bull#bullet;$

   Ein weiteres asymptotisches Konfidenzintervall für $\lambda$ ergibt sich, wenn die Größe $\sqrt{\lambda}$ im Nenner von (30) ersetzt wird durch $\sqrt{\overline X_n}$.

    $&bull#bullet;$

   Aus dem starken Gesetz der großen Zahlen (vgl. Theorem WR-5.15) ergibt sich nämlich, dass

   $$\overline X_n \overset{\textrm{f.s.}}{\longrightarrow} \lambda\,.$$

    $&bull#bullet;$

   Mit Hilfe des Satzes von Slutsky für die Multiplikation (vgl. Theorem WR-5.11) ergibt sich hieraus und aus (30) die Gültigkeit von

   $$\lim\limits _{n\to\infty} P_\lambda\Bigl(-z_{1-\alpha/2}\le\sqrt... ...\overline X_n-\lambda}{\sqrt{\overline X_n}}\le z_{1-\alpha/2}\Bigr)=1-\alpha$$ (32)

   
   

   für jedes $\alpha\in(0,1)$.

    $&bull#bullet;$

   Also ist mit

   $$\underline\theta(X_1,\ldots,X_n)=\overline X_n-\frac{z_{1-\alpha... ...ldots,X_n)=\overline X_n+\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n}$$ (33)

   
   

   ein weiteres asymptotisches Konfidenzintervall $\bigl(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n)\bigr)$ für $\lambda$ zum Niveau $\gamma=1-\alpha$ gegeben.

    $&bull#bullet;$

   Dabei ist allerdings zu beachten, dass die Zufallsvariable $\underline\theta(X_1,\ldots,X_n)$ in (33) auch negative Werte annehmen kann, obwohl bei der Poisson-Verteilung vorausgesetzt wird, dass $\lambda>0$.

    $&bull#bullet;$

   Deshalb kann man anstelle von (33) die Zufallsvariablen

   $$\underline\theta(X_1,\ldots,X_n)=\max\Bigl\{0,\overline X_n-\fra... ...ots,X_n)=\overline X_n+\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n}$$

   als Endpunkte des Konfidenzintervalls $\bigl(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n)\bigr)$ für $\lambda$ betrachten.

    $&bull#bullet;$

   Die Länge dieses Konfidenzintervalls ist stets kleiner als die in (31) gegebene Länge des Intervalls, das aus dem Ansatz (30) resultiert.

    $&bull#bullet;$

   Der Grund hierfür ist, dass ,,untypische'' Stichprobenwerte, die große Abweichungen vom Erwartungswert $\lambda$ aufweisen, besser durch das Stichprobenmittel $\overline X_n$ im Nenner von (32) als durch den Erwartungswert $\lambda$ im Nenner von (30) kompensiert werden.

   
   

2. $\;$ Konfidenzintervall für die ,,Erfolgswahrscheinlichkeit'' $p$ bei Bernoulli-Verteilung
   • Wir nehmen an, dass $X_i\sim$ Bin$(1,p)$ für ein (unbekanntes) $p\in(0,1)$.
   • Weil dann ${\mathbb{E}\,}X_i=p$ und ${\rm Var\,}X_i=p(1-p)$ gilt, ergibt sich aus dem zentralen Grenzwertsatz für Summen von unabhängigen und identisch verteilten Zufallsvariablen (vgl. Theorem WR-5.16), dass für jedes $\alpha\in(0,1)$

     $$\lim\limits _{n\to\infty} P_p\Bigl(-z_{1-\alpha/2}\le\sqrt{n}\;\frac{\overline X_n-p}{\sqrt{p(1-p)}}\le z_{1-\alpha/2}\Bigr)=1-\alpha\,.$$ (34)

     
     

   • Durch Quadrierung der Ungleichungen in (34) und anschließende Auflösung nach $p$ ergibt sich, dass (34) äquivalent ist mit
     $$\lim\limits _{n\to\infty} P_p\bigl(\underline\theta(X_1,\ldots,X_n)\le p\le\overline\theta(X_1,\ldots,X_n) \bigr)=1-\alpha\,,$$
     wobei
     $$\underline\theta(X_1,\ldots,X_n) =\frac{1}{n+z^2_{1-\alpha/2}}\l... ...,\sqrt{n\overline X_n(1-\overline X_n)+ \frac{z^2_{1-\alpha/2}}{4}}\;\right)$$
     bzw.
     $$\overline\theta(X_1,\ldots,X_n) =\frac{1}{n+z^2_{1-\alpha/2}}\le... ...qrt{n\overline X_n(1-\overline X_n)+ \frac{z^2_{1-\alpha/2}}{4}}\;\right)\,.$$

   • Auf diese Weise ergibt sich ein asymptotisches Konfidenzintervall $\bigl(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n)\bigr)$ für $p$ zum Niveau $\gamma=1-\alpha$.

   Beachte

    $&bull#bullet;$

   Ähnlich wie in dem vorhergehenden Beispiel erhält man ein einfacheres asymptotisches Konfidenzintervall für $p$, wenn man berücksichtigt, dass wegen des starken Gesetzes der großen Zahlen (vgl. Theorem WR-5.15)

   $$\overline X_n \overset{\textrm{f.s.}}{\longrightarrow} p\,.$$

    $&bull#bullet;$

   Hieraus und aus (34) ergibt sich nun mit Hilfe des Satzes von Slutsky für die Multiplikation (vgl. Theorem WR-5.11), dass

   $$\lim\limits _{n\to\infty} P_p\Bigl(-z_{1-\alpha/2}\le\sqrt{n}\;\... ...-p}{\sqrt{\overline X_n(1-\overline X_n)}}\le z_{1-\alpha/2}\Bigr)=1-\alpha\,.$$ (35)

   
   

    $&bull#bullet;$

   Also ist mit

   $$\underline\theta(X_1,\ldots,X_n)=\overline X_n-\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n(1-\overline X_n)}$$

   bzw.

   $$\overline\theta(X_1,\ldots,X_n)= \overline X_n+\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n(1-\overline X_n)}$$

   ein weiteres asymptotisches Konfidenzintervall $\bigl(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n)\bigr)$ für $p$ zum Niveau $\gamma=1-\alpha$ gegeben.

    $&bull#bullet;$

   Dabei ist jedoch zu beachten, dass die Zufallsvariable $\underline\theta(X_1,\ldots,X_n)$ negative Werte und $\overline\theta(X_1,\ldots,X_n)$ Werte größer als 1 annehmen kann, obwohl bei der Bernoulli-Verteilung vorausgesetzt wird, dass $0<p<1$.

    $&bull#bullet;$

   Deshalb betrachtet man die modifizierten Schätzer

   $$\underline\theta(X_1,\ldots,X_n)=\max\Bigl\{0,\overline X_n-\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n(1-\overline X_n)}\Bigr\}$$

   bzw.

   $$\overline\theta(X_1,\ldots,X_n)= \min\Bigl\{1,\overline X_n+\frac{z_{1-\alpha/2}}{\sqrt{n}}\,\sqrt{\overline X_n(1-\overline X_n)}\Bigr\}$$

   als Endpunkte des Konfidenzintervalls $(\underline\theta(X_1,\ldots,X_n),\overline\theta(X_1,\ldots,X_n))$ für $p$.