Stichprobenmittel

Wir diskutieren zunächst die Frage, wie der Erwartungswert $\mu={\mathbb{E}\,}X_i$ der Stichprobenvariablen $X_1,\ldots,X_n$ aus den beobachteten Daten $x_1,\ldots,x_n$ bestimmt werden kann.

• Hierfür betrachten wir die Stichprobenfunktion $\varphi:\mathbb{R}^n\to\mathbb{R}$ mit $\varphi(x_1,\ldots,x_n)=n^{-1}\sum_{i=1}^n x_i$.
• D.h., wir betrachten das arithmetische Mittel

  $$\overline x_n=\frac{1}{n}\sum\limits _{i=1}^n x_i$$ (1)

  
  
  der Stichprobenwerte $x_1,\ldots,x_n$.
• Die Zahl $\overline x_n$ wird Stichprobenmittel der (konkreten) Stichprobe $(x_1,\ldots,x_n)$ genannt.
• Außerdem betrachten wir das arithmetische Mittel der Stichprobenvariablen $X_1,\ldots,X_n$, dessen Eigenschaften bereits in Abschnitt WR-5.2 im Zusammenhang mit dem Gesetz der großen Zahlen untersucht worden sind.

Definiton

$\;$ Die Zufallsvariable

$$\overline X_n=\frac{1}{n}\sum\limits _{i=1}^n X_i$$ (2)

heißt Stichprobenmittel der Zufallsstichprobe $(X_1,\ldots,X_n)$.

Der Erwartungswert und die Varianz von $\overline X_n$ lassen sich wie folgt darstellen.

Theorem 1.1   Es gilt

$${\mathbb{E}\,}\overline X_n=\mu$$ (3)

und

$${\rm Var\,}\overline X_n=\frac{\sigma^2}{n}\;,$$ (4)

wobei $\mu={\mathbb{E}\,}X_i$ und $\sigma^2={\rm Var\,}X_i$ den Erwartungswert bzw. die Varianz der Stichprobenvariablen $X_1,\ldots,X_n$ bezeichnen.

Beweis

 

• Die Formeln (3) und (4) ergeben sich wie folgt aus den Theoremen WR-4.4 bzw. WR-4.10.
• Wegen der Linearität des Erwartungswertes gilt nämlich (vgl. Theorem WR-4.4)
  

  $${\mathbb{E}\,}\overline X_n = {\mathbb{E}\,}\Bigl(\frac{1}{n}\sum\limits _{i=1}^n X_i\Bigr)$$

  $$= \frac{1}{n}\sum\limits _{i=1}^n {\mathbb{E}\,}X_i$$

  $$= \frac{1}{n}\sum\limits _{i=1}^n \mu =\mu\,.$$

  
  

• Aus Theorem WR-4.10 über die Varianz der Summe von unabhängigen Zufallsvariablen ergibt sich, dass
  

  $${\rm Var\,}\overline X_n = \frac{1}{n^2}\;{\rm Var\,}\Bigl(\sum\limits _{i=1}^n X_i\Bigr)$$

  $$= \frac{1}{n^2}\;\sum\limits_{i=1}^n {\rm Var\,}X_i$$

  $$= \frac{1}{n^2}\;\sum\limits_{i=1}^n \sigma^2= \frac{\sigma^2}{n}\;.$$

  
  
  
   
    $\Box$
  
  
  

Beachte

 

• Weil das Stichprobenmittel $\overline X_n$ den Erwartungswert $\mu$ hat (vgl. (3)), kann man $\overline X_n$ als einen geeigneten ,,Schätzer'' der (im allgemeinen unbekannten) Modellcharakteristik $\mu$ ansehen.
• Wegen (3) sagt man, dass bei der Schätzung von $\mu$ durch $\overline X_n$ kein ,,systematischer Fehler'' begangen wird.
• Der Schätzer $\overline X_n$ kann dennoch sehr ungenau sein, wobei man den in (4) gegebenen Wert $\sigma^2/n$ als Kennzahl für die Schätzgenauigkeit von $\overline X_n$ auffassen kann.
• Dabei bedeutet (4), dass die Schätzgenauigkeit mit wachsendem Stichprobenumfang $n$ verbessert wird.
• Es ist jedoch zu beachten, dass $\sigma^2$ im allgemeinen ebenfalls unbekannt ist.
• Um eine Vorstellung über die Größenordnung der Schätzgenauigkeit von $\overline X_n$ bei vorgegebenem Stichprobenumfang $n$ zu erlangen, muss deshalb auch $\sigma^2$ aus den beobachteten Daten $x_1,\ldots,x_n$ geschätzt werden.
• Diese Fragestellung werden wir in Abschnitt 1.2.2 diskutieren.

Neben den Formeln (3) und (4) für Erwartungswert und Varianz des Stichprobenmittels $\overline X_n$ sind noch weitere Aussagen über die Verteilung von $\overline X_n$ von Interesse bzw. über deren asymptotisches Verhalten für große $n$.

Theorem 1.2   Es gilt

$$P\Bigl(\lim\limits _{n\to\infty} \overline X_n =\mu\Bigr)=1$$ (5)

und

$$\lim\limits _{n\to\infty}P\Bigl(\sqrt{n}\; \frac{\overline X_n -\mu}{\sigma}\le x\Bigr)=\Phi(x)$$ (6)

für jedes $x\in\mathbb{R}$, wobei $\Phi(x)$ die Verteilungsfunktion der Standardnormalverteilung ist.

Der Beweis von Theorem 1.2 ergibt sich unmittelbar aus dem starken Gesetz der großen Zahlen bzw. aus dem zentralen Grenzwertsatz für Summen von unabhängigen und identisch verteilten Zufallsvariablen (vgl. die Theoreme WR-5.15 bzw. WR-5.16).

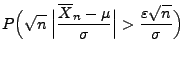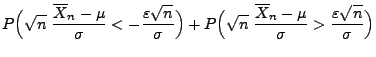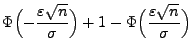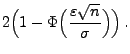Beachte

 

• Theorem 1.2 bietet eine Möglichkeit, um die Wahrscheinlichkeit des Ereignisses $\{\vert\overline X_n-\mu\vert>\varepsilon\}$ zu bestimmen, dass das Stichprobenmittel $\overline X_n$ um mehr als einen vorgegebenen Schwellenwert $\varepsilon>0$ von dem zu schätzenden Wert $\mu$ abweicht.
• Aus (6) ergibt sich hierfür die folgende Näherungsformel

  $$P(\vert\overline X_n-\mu\vert>\varepsilon)\approx 2\Bigl(1-\Phi\Bigl(\frac{\varepsilon\sqrt{n}}{\sigma}\Bigr)\Bigr)$$ (7)

  
  
  für große $n$, denn es gilt
  

  $$P(\vert\overline X_n-\mu\vert>\varepsilon) = P\Bigl(\sqrt{n}\; \Bigl\vert\frac{\overline X_n -\mu}{\sigma}\Bigr\vert>\frac{\varepsilon\sqrt{n}}{\sigma} \Bigr)$$

  $$= P\Bigl(\sqrt{n}\; \frac{\overline X_n -\mu}{\sigma}<-\frac{\varep... ...}\; \frac{\overline X_n -\mu}{\sigma}>\frac{\varepsilon\sqrt{n}}{\sigma} \Bigr)$$

  $$\stackrel{(\ref{cen.sti.mit})}{\approx} \Phi\Bigl(-\frac{\varepsilon\sqrt{n}}{\sigma}\Bigr)+1 -\Phi\Bigl(\frac{\varepsilon\sqrt{n}}{\sigma}\Bigr)$$

  $$= 2\Bigl(1-\Phi\Bigl(\frac{\varepsilon\sqrt{n}}{\sigma}\Bigr)\Bigr)\,.$$

  
  

• Falls $\sigma^2$ unbekannt ist, dann kann man anstelle der Näherungsformel (7) ein (zufälliges) Intervall angeben, in dem die Abweichung $\overline X_n-\mu$ des Stichprobenmittels $\overline X_n$ von dem zu schätzenden Wert $\mu$ mit einer (näherungsweise) vorgegebenen Wahrscheinlichkeit liegt, vgl. die Anmerkungen am Ende von Abschnitt 1.2.2.