- A simple computer algorithm for the Monte-Carlo simulation of
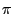 is the following improved version of Buffon's needle
experiment; see Sections 2.5 and 5.2.3 of the course
,,Wahrscheinlichkeitsrechnung''.
is the following improved version of Buffon's needle
experiment; see Sections 2.5 and 5.2.3 of the course
,,Wahrscheinlichkeitsrechnung''.
This algorithm is based on the following geometrical facts.
- We consider the square
![$\displaystyle B=(-1,1]\times(-1,1]\subset\mathbb{R}^2\,,
$](img1032.png)
- the circle
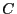 inscribed into
inscribed into 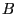 , where
, where
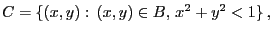
- and arbitrarily toss a point
into the set
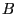 .
.
- We consider the square
- Translated into the language of stochastics this means:
- We consider two independent random variables
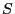 and
and 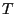 that are uniformly distributed on the
interval
that are uniformly distributed on the
interval ![$ (-1,1]$](img901.png) and
and
- determine the probability of the event
i.e. that the ,,random point''
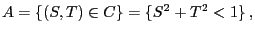
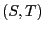 is in
is in
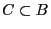 .
.
- Then
where
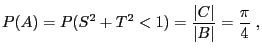
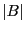 and
and 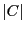 denote the area of
denote the area of 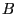 and
and
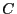 , respectively.
, respectively.
- We consider two independent random variables
- Similarly to Buffon's needle experiment
the equation
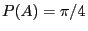 yields a
yields a
- method for the statistical estimation of
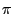 ,
,
- which is based on the strong law of large numbers (SLLN) and can be easily implemented.
- method for the statistical estimation of
- Let
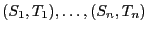 be independent and identically distributed
random vectors,
be independent and identically distributed
random vectors,
- whose distribution coincides with the one of
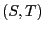
- and which are regarded as a stochastic model for
 (independent) experiments.
(independent) experiments.
- Then
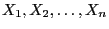 where
are independent and identically distributed random variables with expectation
where
are independent and identically distributed random variables with expectation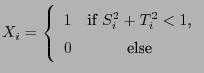
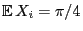 .
.
- whose distribution coincides with the one of
- Furthermore, the SLLN (see Theorem WR-5.15)
implies
- that the arithmetic mean
converges to
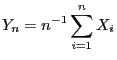
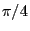 almost surely.
almost surely.
- Thus,
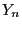 is an unbiased and (strongly)
consistent estimator for
is an unbiased and (strongly)
consistent estimator for
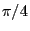 ,
,
- i.e., the probability of
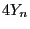 to be a good approximation for
to be a good approximation for 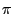 is very high if
is very high if  is large.
is large.
- that the arithmetic mean
- For the implementation of this simulation algorithm one can
proceed as follows
- Use a random number generator to generate
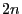 pseudo-random
numbers
pseudo-random
numbers
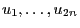 that are realizations of random variables being uniformly distributed on
that are realizations of random variables being uniformly distributed on ![$ (0,1]$](img165.png) .
.
- Put
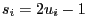 and
and
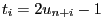 for
for
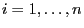 .
.
- Define
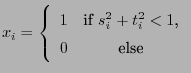
- Compute
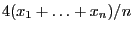 .
.
- Use a random number generator to generate
- Let
![$ \varphi:[0,1]\to[0,1]$](img1058.png) be a continuous function.
be a continuous function.
- Our goal is to find an estimator for the value of the integral
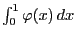 that can be determined by Monte-Carlo
simulation.
that can be determined by Monte-Carlo
simulation.
- We consider the following stochastic model.
- Our goal is to find an estimator for the value of the integral
- Let the random variables
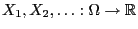 be
independent and uniformly distributed on
be
independent and uniformly distributed on ![$ (0,1]$](img165.png) , with probability
density
, with probability
density 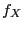 given by
given by
![$\displaystyle f_X(x)=\left\{\begin{array}{ll} 1 &\mbox{if $x\in[0,1]$,}\\
0 & \mbox{else.}
\end{array}\right.
$](img1062.png)
- Let
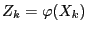 for all
for all
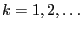 .
.
- By the transformation theorem for independent and identically
distributed random variables (see Theorem WR-3.18) the random
variables
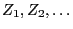 are independent and identically
distributed
are independent and identically
distributed
- with
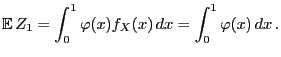
- Let
- Furthermore the SSLN (see Theorem WR-5.15) implies that for
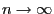
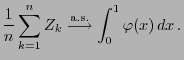
- Hence
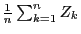 is an unbiased and
(strongly) consistent estimator for
is an unbiased and
(strongly) consistent estimator for
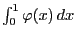 ,
,
- i.e., the probability for
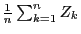 to be a
good approximation of the integral
to be a
good approximation of the integral
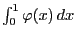 is high for sufficiently large
is high for sufficiently large  .
.
- Hence
- For the implementation of this simulation algorithm one can
proceed similarly to Example 1:
- Use a random number generator to generate
 pseudo-random numbers
pseudo-random numbers
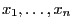 that are realizations of random variables being uniformly distributed in
that are realizations of random variables being uniformly distributed in ![$ (0,1]$](img165.png) .
.
- Define
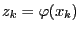 for
for
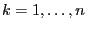 .
.
- Compute
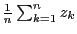 .
.
- Use a random number generator to generate